第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. [2025年1月淮北期末]如图,已知∠E= ∠F= 90°,∠B= ∠C,AE= AF,下列结论:①EM= FN;②CM= EM;③∠FAN= ∠EAM;④△ACN≌ABM,其中正确的有(
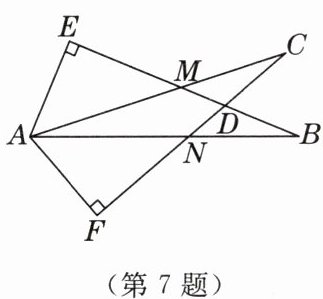
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:
C
8. 数形结合思想 [2025年1月安庆期末]如图,在△ACB中,∠ACB= 90°,AC= BC,点C的坐标为(-1,0),点A的坐标为(-6,3),则B点的坐标是
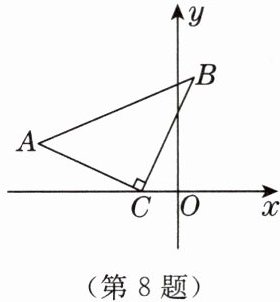
(2,5)
.
答案:
(2,5)
9. 如图,在△ABC中,AD是边BC上的中线,E是边AB上一点,过点C作CF//AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE= 1,CF= 2时,求AC的长.
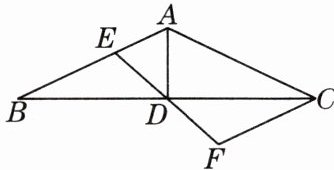
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE= 1,CF= 2时,求AC的长.

答案:
(1)证明:
∵CF//AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是边BC上的中线,
∴BD=CD,
∴△BDE≌△CDF(AAS).
(2)解:AC=3.
(1)证明:
∵CF//AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是边BC上的中线,
∴BD=CD,
∴△BDE≌△CDF(AAS).
(2)解:AC=3.
10. 中考趋势·探究建模 [探究发现]
(1)如图①,△ABC中,H是高AD和高BE的交点,则∠HBD与∠CAD的大小关系是______;
[拓展运用]
(2)如图①,△ABC中,H是高AD和高BE的交点,且AD= BD,请你猜想BH和AC的数量关系,并说明理由;
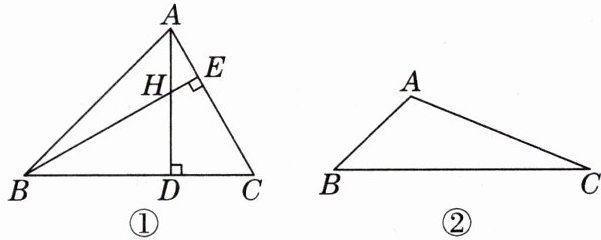
[知识迁移]
(3)若将图①中的∠BAC改成钝角,H是高AD和高BE所在直线的交点,且AD= BD,请你在图②中画出该题的图形,此时(1)(2)中的结论还成立吗?为什么?
(1)如图①,△ABC中,H是高AD和高BE的交点,则∠HBD与∠CAD的大小关系是______;
[拓展运用]
(2)如图①,△ABC中,H是高AD和高BE的交点,且AD= BD,请你猜想BH和AC的数量关系,并说明理由;

[知识迁移]
(3)若将图①中的∠BAC改成钝角,H是高AD和高BE所在直线的交点,且AD= BD,请你在图②中画出该题的图形,此时(1)(2)中的结论还成立吗?为什么?
答案:
解:
(1)∠HBD=∠CAD
(2)BH=AC.理由如下:
∵AD,BE都是△ABC的高,
∴∠ADC=∠ADB=∠AEH=90°.
∴∠DAC+∠C=∠EBC+∠C=90°,
∴∠DAC=∠EBC.
∵AD=BD,
∴△BDH≌△ADC,
∴BH=AC.
(3)如图所示,
(1)
(2)中的结论仍成立,即∠HBD=∠CAD,BH=AC.理由如下:
∵AD和BE是△ABC的高,
∴∠BDH=∠ADC=∠BEC=90°,
∴∠DBH+∠H=∠DBH+∠C=90°,
∴∠H=∠C.又
∵BD=AD,
∴△BDH≌△ADC,
∴∠HBD=∠CAD,BH=AC.
解:
(1)∠HBD=∠CAD
(2)BH=AC.理由如下:
∵AD,BE都是△ABC的高,
∴∠ADC=∠ADB=∠AEH=90°.
∴∠DAC+∠C=∠EBC+∠C=90°,
∴∠DAC=∠EBC.
∵AD=BD,
∴△BDH≌△ADC,
∴BH=AC.
(3)如图所示,
(1)
(2)中的结论仍成立,即∠HBD=∠CAD,BH=AC.理由如下:
∵AD和BE是△ABC的高,
∴∠BDH=∠ADC=∠BEC=90°,
∴∠DBH+∠H=∠DBH+∠C=90°,
∴∠H=∠C.又
∵BD=AD,
∴△BDH≌△ADC,
∴∠HBD=∠CAD,BH=AC.

查看更多完整答案,请扫码查看


