《2025年点拨训练八年级数学上册沪科版安徽专版》

2星题 中档练
8. [2025年1月淮南期末]对于一次函数$y = - 2x + 6$的图象及性质,下列结论正确的是(A)
A.图象与$y = - 2x + 1$的图象平行
B.$y随x$的增大而增大
C.图象经过第一、二、三象限
D.图象过点$(-3, 0)$

答案： A

9. [2024·福州期末]已知函数$y = (2m - 4)x + m^2 - 9$($x$是自变量)的图象只经过第二、四象限,则$m$的值为(B)
A.3
B.$-3$
C.9
D.$-9$

答案： B

10. 若一次函数$y = kx + 3的自变量x$的取值每增加2,函数值$y$就相应减少4,则$k$的值为(C)
A.2
B.$-1$
C.$-2$
D.4

答案： C

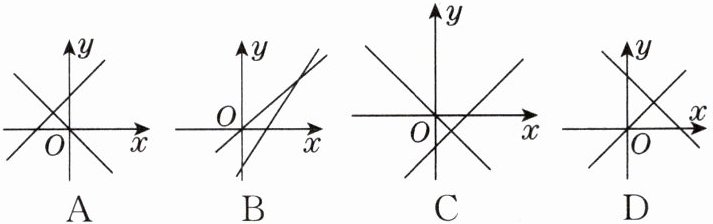
11. 一次函数$y = mx + n与正比例函数y = mnx$($m$,$n$为常数,且$mn \neq 0$)在同一平面直角坐标系中的图象可能是(C)

答案： C

12. 已知点$(-4, y_1)$,$(2, y_2)$,$(-2, y_3)都在直线y = - \frac{2}{3}x - b$上,则$y_1$,$y_2$,$y_3$的大小关系为y₂＜y₃＜y₁。(用“$＜$”连接)

答案： y₂＜y₃＜y₁

13. 已知一次函数$y = - \frac{1}{2}x + 3$,当$-3 \leq x \leq 4$时,$y$的最大值是$\frac{9}{2}$。

答案： $\frac{9}{2}$

14. 已知一次函数$y = mx - (m - 2)$。
(1)若该函数图象过点$(0, 3)$,则$m = $-1；
(2)若该函数图象经过第一、二、四象限,则$m$的取值范围是什么？
(3)若该函数图象不经过第四象限,则$m$的取值范围是什么？

答案：
(1)-1　
(2)m的取值范围是m＜0.
(3)m的取值范围是0＜m≤2.

3星题 提升练
15. 学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法。小聪同学尝试运用积累的经验和方法对函数$y = |x - 1| - 2$的图象与性质进行探究,下面是小聪同学的探究过程,请你补充完整。
(1)列表：

则$a = $______,$b = $______。
(2)描点并画出该函数的图象。
(3)①请写出一条关于函数$y = |x - 1| - 2$的性质：______；
②观察函数图象,当$2 ＜ y ＜ 4$时,$x$的取值范围是______；
③观察函数图象,可得函数$y = |x - 1| - 2$的最小值为______。

答案：

(1)-1；0
(2)如图所示.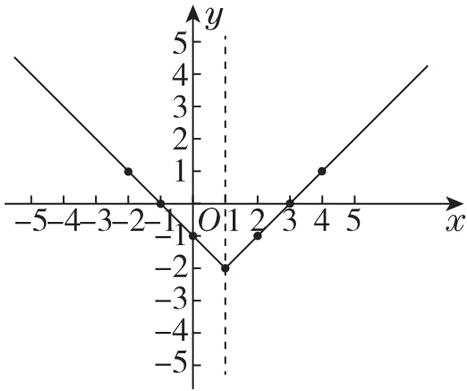
(3)①当x＞1时，y随x的增大而增大(答案不唯一)②-5＜x＜-3或5＜x＜7　③-2