《2025年点拨训练八年级数学上册沪科版安徽专版》

10. 若点$A(m-1,2m+2)$到x轴和y轴的距离相等,则$m=$$-3$或$-\frac{1}{3}$.

答案： 【解析】：
本题主要考查点到坐标轴的距离公式。
点到x轴的距离等于该点的y坐标的绝对值，点到y轴的距离等于该点的x坐标的绝对值。
根据题意，点$A(m-1,2m+2)$到x轴和y轴的距离相等，
即$|m-1| = |2m+2|$。
解这个绝对值方程，我们得到两个可能的
$m-1 = 2m+2$ 或 $m-1 = -(2m+2)$。
解第一个方程 $m-1 = 2m+2$，得到 $m = -3$。
解第二个方程 $m-1 = -(2m+2)$，得到 $m = -\frac{1}{3}$。
【答案】：
$m = -3$ 或 $m = -\frac{1}{3}$。

11. [2024·芜湖期中]对于平面直角坐标系中的任意一点$P(x,y)$,给出如下定义：记$a= -x$,$b= x-y$,那么我们把点$M(a,b)与点N(b,a)$称为点P的一对“和谐点”.例如,点$P(-1,2)$的一对“和谐点”是点$(1,-3)与点(-3,1)$.
(1)若点$B(3,y)$的一对“和谐点”重合,则y的值为6；
(2)若点C的一个“和谐点”的坐标为$(-2,9)$,则点C的坐标为$(2,-7)$或$(-9,-7)$.

答案：
(1)解：由题意得，点$B(3,y)$中$x = 3$，则$a=-x=-3$，$b=x - y=3 - y$。
所以点$M(a,b)=(-3,3 - y)$，点$N(b,a)=(3 - y,-3)$。
因为点$M$与点$N$重合，所以它们的横纵坐标分别相等，即：
$\begin{cases}-3=3 - y\\3 - y=-3\end{cases}$
由$-3=3 - y$，解得$y=6$。
(2)解：设点$C$的坐标为$(x,y)$，则$a=-x$，$b=x - y$，点$C$的一对“和谐点”为$M(a,b)=(-x,x - y)$和$N(b,a)=(x - y,-x)$。
已知点$C$的一个“和谐点”的坐标为$(-2,9)$，分两种情况：
情况一：若$M(-x,x - y)=(-2,9)$，则：
$\begin{cases}-x=-2\\x - y=9\end{cases}$
由$-x=-2$，得$x=2$。
将$x=2$代入$x - y=9$，得$2 - y=9$，解得$y=-7$。
所以点$C$的坐标为$(2,-7)$。
情况二：若$N(x - y,-x)=(-2,9)$，则：
$\begin{cases}x - y=-2\\-x=9\end{cases}$
由$-x=9$，得$x=-9$。
将$x=-9$代入$x - y=-2$，得$-9 - y=-2$，解得$y=-7$。
所以点$C$的坐标为$(-9,-7)$。
综上，点$C$的坐标为$(2,-7)$或$(-9,-7)$。
(1) $6$；
(2) $(2,-7)$或$(-9,-7)$

12. 创新题·探究题如图,马鞍山某小区绿化区的护栏由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,$A_1的坐标为(2,2)$,$A_2的坐标为(5,2)$,则$A_3$的坐标为____,$A_n$的坐标为____(用含n的代数式表示).

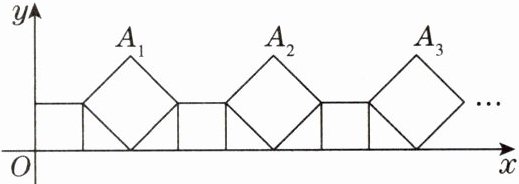
补充设问 若护栏长为2025,则需要小正方形____个,大正方形____个.
(8,2)(3n - 1,2)675674

答案： 【解析】：
本题主要考查了点的坐标规律探索及代数式求值。
对于$A_3$的坐标：
观察图形可知，$A_1$的坐标为$(2,2)$，$A_2$的坐标为$(5,2)$，由于这些点都在平行于$x$轴的直线上（$y=2$），且相邻两点间的水平距离为小正方形边长与大正方形边长之和，已知小正方形边长为$1$，从图中可看出大正方形边长为$2$，那么相邻两点水平距离为$1 + 2 = 3$。
$A_1$到$A_2$水平距离是$3$，$A_2$到$A_3$水平距离同样是$3$，$A_2$横坐标为$5$，所以$A_3$横坐标为$5 + 3 = 8$，纵坐标不变仍为$2$，即$A_3$的坐标为$(8,2)$。
对于$A_n$的坐标：
$A_1$横坐标为$2$，$A_2$横坐标为$2 + 3×1 = 5$，$A_3$横坐标为$2 + 3×2 = 8$，以此类推，$A_n$的横坐标为$2 + 3×(n - 1)$，根据乘法分配律$a×(b - c)=a× b - a× c$，$2 + 3×(n - 1)=2 + 3n - 3 = 3n - 1$，纵坐标始终为$2$，所以$A_n$的坐标为$(3n - 1,2)$。
对于护栏长为$2025$时小正方形和大正方形的个数：
观察图形可知，一个循环单元（一个小正方形和一个大正方形）的长度为$1 + 2 = 3$。
设共有$x$个循环单元，余下长度为$1$（因为最后一个是小正方形），可列方程$3x + 1 = 2025$，
移项可得$3x = 2025 - 1 = 2024$，
解得$x=\frac{2024}{3}$（舍去，因为$x$必须为整数），这里我们换一种思路，$(2025 - 1)÷3 = 674\cdots\cdots2$，我们发现如果从护栏组成规律看，$2025 = 674×3 + 2 + 1$（$674$个循环单元，再加上最后一个小正方形和一个大正方形的一部分，而实际组成完整护栏时，是$674 + 1 = 675$个小正方形，$674$个大正方形）。
下面我们严格推导：
设小正方形有$m$个，大正方形有$n$个，因为除最后一个单独的小正方形外，前面是$(m - 1)$个小正方形和$n$个大正方形组成循环结构，且一个循环结构长度为$3$，所以$3n + 1+(m - n)=2025$（$3n$是$n$个循环结构中大正方形和小正方形组合的长度，$1$是最后一个小正方形多出来的部分占一个单位长度，$m - n$是除去循环结构中与大正方形对应搭配的小正方形后剩下的小正方形个数，这里$m - n = 1$时就是最后一个小正方形），又因为从组成规律看$m=n + 1$，代入$3n+1+(m - n)=2025$得$3n + 1 + 1=2025$，$3n=2023$（错误），我们重新根据图形规律，把护栏长度看作是由若干个$(1 + 2)$的长度组合再加上一个小正方形长度，即$2025-1=2024$，$2024÷3 = 674\cdots\cdots2$，实际小正方形个数$m = 674 + 1=675$，大正方形个数$n = 674$。
【答案】：
$(8,2)$；$(3n - 1,2)$；$675$；$674$。

13. 创新题·新考法已知四边形ABCD四个顶点的坐标分别为$A(0,2)$,$B(-1,0)$,$C(2,0)$,$D(1,2)$,李轩把四边形ABCD平移后得到了四边形EFGH,它的四个顶点的坐标分别为$E(1,1)$,$F(0,-1)$,$G(3,1)$,$H(2,1)$,数学老师看后发现只有一个顶点的坐标写错了,则李轩写错坐标的顶点为G.

答案： 【解析】：
首先，我们观察四边形ABCD和四边形EFGH的顶点坐标。
对于顶点A和E，A的坐标为$(0,2)$，E的坐标为$(1,1)$。变化为向右平移1个单位，向下平移1个单位。
对于顶点B和F，B的坐标为$(-1,0)$，如果按照A到E的平移方式，F的坐标应为$(0,-1)$，与给定的F坐标相符。
对于顶点C和G，C的坐标为$(2,0)$，如果按照A到E的平移方式，G的坐标应为$(3,-1)$，但给定的G的坐标为$(3,1)$，这里存在差异。
对于顶点D和H，D的坐标为$(1,2)$，如果按照A到E的平移方式，H的坐标应为$(2,1)$，与给定的H坐标相符。
从上面的分析中，我们可以看出，只有顶点G的坐标与预期的平移结果不符。按照A到E的平移方式，G的坐标应该是$(3,-1)$，而不是$(3,1)$。
【答案】：
G

14. 分类讨论思想已知点P的坐标为$(1,2)$,线段PQ平行于y轴且$PQ= 5$,则点Q的坐标为(B)
A.$(6,2)$
B.$(1,7)或(1,-3)$
C.$(1,7)$
D.$(-4,2)或(6,2)$

答案： 【解析】：
本题主要考查了坐标系中点的坐标确定以及平行于坐标轴的线段性质。
由于线段$PQ$平行于$y$轴，根据坐标系的性质，我们知道平行于$y$轴的线段上的所有点的横坐标都相同。
因此，点$Q$的横坐标必须与点$P$的横坐标相同，即$Q_x = 1$。
接下来，我们需要确定点$Q$的纵坐标。
由于$PQ$的长度为5，我们可以分两种情况来考虑点$Q$的位置：
如果$Q$在$P$的上方，那么$Q$的纵坐标应该是$P$的纵坐标加上$PQ$的长度，即$Q_y = 2 + 5 = 7$。
如果$Q$在$P$的下方，那么$Q$的纵坐标应该是$P$的纵坐标减去$PQ$的长度，即$Q_y = 2 - 5 = -3$。
综合以上分析，我们可以得出点$Q$的两个可能的坐标是$(1,7)$和$(1,-3)$。
【答案】：
B. $(1,7)$或$(1,-3)$。

15. 方程思想在平面直角坐标系中,已知点$M(a-4,2a+1)$.
(1)若点M的横坐标与纵坐标相等,则点M的坐标为$(-9,-9)$；
(2)若点M在过点$N(3,-3)$且与x轴平行的直线上,则点M的坐标为$(-6,-3)$.

答案： 【解析】：
本题主要考查平面直角坐标系中点的坐标性质以及一元一次方程的解法。
(1) 对于点M的横坐标与纵坐标相等的情况，我们可以根据这一性质列出方程，然后求解得到a的值，从而确定点M的坐标。
(2) 对于点M在过点N且与x轴平行的直线上的情况，我们可以根据这一性质知道点M的纵坐标与点N的纵坐标相等，从而列出方程求解a的值，确定点M的坐标。
【答案】：
(1)
由于点M的横坐标与纵坐标相等，所以有：
$a - 4 = 2a + 1$，
移项得：
$-a = 5$，
从而解得：
$a = -5$，
将$a = -5$代入点M的坐标表达式，得到：
$M(-9, -9)$；
(2)
由于点M在过点N且与x轴平行的直线上，所以点M的纵坐标与点N的纵坐标相等，即：
$2a + 1 = -3$，
移项并化简得：
$2a = -4$，
从而解得：
$a = -2$，
将$a = -2$代入点M的坐标表达式，得到：
$M(-6, -3)$。

16. 分类讨论思想如图,在平面直角坐标系中,四边形OABC为正方形,且边长为4,点A在x轴负半轴上,点C在y轴负半轴上.有一动点P自点O出发,以每秒2个单位的速度沿$O→A→B→C→O$运动,何时$S_{三角形PBC}= 4$？求出此时点P的坐标.

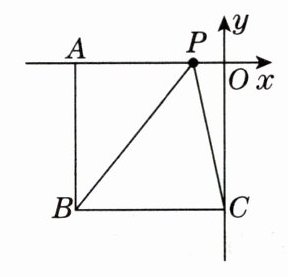
答案： 解：由题意得，正方形OABC边长为4，点A(-4,0)，B(-4,-4)，C(0,-4)。
情况1：P在OA上（0≤t≤2）
P(2t-4,0)，PB=4，BC=4，
S△PBC=1/2×BC×|x_P - x_B|=1/2×4×|2t-4 - (-4)|=2×|2t|=4|t|=4
解得t=1（t=-1舍），此时P(-2,0)。
情况2：P在AB上（2＜t≤4）
P(-4,2t-8)，△PBC以BC为底，高为0，S=0≠4，无解。
情况3：P在BC上（4＜t≤6）
P(2t-12,-4)，S△PBC=1/2×BC×|x_C - x_P|=1/2×4×|0 - (2t-12)|=2×|12-2t|=4|6-t|=4
解得t=5（t=7舍），此时P(-2,-4)。
情况4：P在CO上（6＜t≤8）
P(0,16-2t)，△PBC以BC为底，高为0，S=0≠4，无解。
综上，t=1时，P(-2,0)；t=5时，P(-2,-4)。
答案：t=1秒时，P(-2,0)；t=5秒时，P(-2,-4)。

17. [2024·合肥三模]若点$P(a+1,a+3)$在第二象限,则a的取值范围是$-3 ＜ a ＜ -1$.

答案： 【解析】：
本题主要考查了各象限内点的坐标的符号特征以及解一元一次不等式组的方法。
记住各象限内点的坐标的符号是解题的关键，四个象限的符号特点分别是：第一象限$(+,+)$；第二象限$(-,+)$；第三象限$(-,-)$；第四象限$(+,-)$。
根据第二象限内点的坐标特征，得到关于$a$的一元一次不等式组：
$\left\{ \begin{array}{l} a + 1 ＜ 0 \\a + 3 ＞ 0 \end{array} \right.$
解第一个不等式$a + 1 ＜ 0$，得$a ＜ -1$；
解第二个不等式$a + 3 ＞ 0$，得$a ＞ -3$；
综合两个不等式的解，得到$a$的取值范围为$-3 ＜ a ＜ -1$。
【答案】：
$-3 ＜ a ＜ -1$