《2025年点拨训练八年级数学上册沪科版安徽专版》

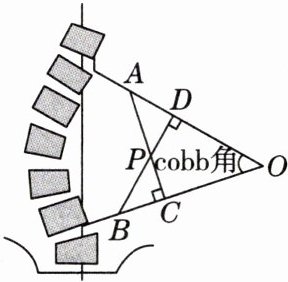
8. 真实情境如图,这是脊柱侧弯测量显示的示意图,cobb角$(∠O)$是一个测量侧弯曲角度的方法,用于评估脊柱侧弯的严重程度,当cobb角$＞10^{\circ }$时为脊柱侧弯.已知$AC⊥BO,BD⊥AO,CO= DO,AD= BC$.
(1)$△ACO与△BDO$全等吗?请说明理由.
(2)若小明是轻度脊柱侧弯$(10^{\circ }＜∠O＜25^{\circ })$,写出图中与$∠O$相等的角:∠APD，∠BPC.

答案： 解：
(1)△ACO与△BDO全等，理由如下：
∵AC⊥BO，BD⊥AO，
∴∠ACO=∠BDO=90°.
∵CO=DO，AD=BC，
∴OD+AD=OC+CB，即OA=OB，
∴Rt△ACO≌Rt△BDO(HL).
(2)∠APD，∠BPC

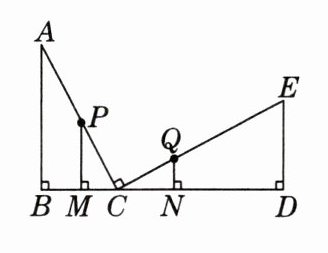
9. 分类讨论思想如图,点C在线段BD上,$AB⊥BD$于点B,$ED⊥BD$于点D,$∠ACE= 90^{\circ }$,且$AC= 5cm,CE= 6cm$,点P从点A开始以$2cm/s$的速度沿AC向终点C运动,同时点Q以$3cm/s$的速度从点E出发,沿$E→C→E$运动,当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足分别为M,N.设运动的时间为t s,当以P,C,M三点为顶点的三角形与$△QCN$全等时,t的值为 (C)

A.1

B.1或2
C.1或$\frac {11}{5}$
D.1或$\frac {11}{5}或\frac {23}{5}$

答案： C

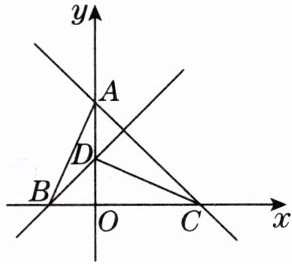
10. 数形结合思想[2025年1月淮北期末]如图,直线$y= -x+4$与坐标轴交于A,C两点,直线$y= x+2$与坐标轴交于B,D两点,连接AB,CD.试说明$AB= CD$.

答案： 解：对于函数y=-x+4，
令x=0，则y=4；令y=0，则x=4，
∴A(0,4)，C(4,0)，
∴AO=CO=4.
对于函数y=x+2，
令x=0，则y=2；令y=0，则x=-2，
∴B(-2,0)，D(0,2)，
∴BO=DO=2.
∵∠AOB=∠COD=90°，
∴△ABO≌△CDO，
∴AB=CD.

11. 我们知道“两边及其中一边的对角分别对应相等的两个三角形不一定全等”.但是,乐乐发现:当这两个三角形都是锐角三角形时,它们会全等.
(1)乐乐的说法是正确的(填“正确”或“不正确”);
(2)除乐乐的发现之外,当这两个三角形都是钝角三角形或直角三角形时,它们也会全等.

答案：
(1)正确
(2)钝角三角形或直角三角形

12. [2024·合肥二模]如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的$△ABC$.

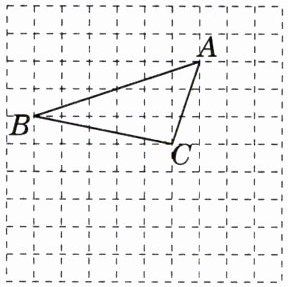
(1)将$△ABC$向右平移2个单位,再向下平移3个单位得到$△DEF$(其中A与D,B与E,C与F是对应点),在网格中画出$△DEF$;
(2)用无刻度直尺在网格中画出AC边上的高BH.

答案： 【解析】：
（1）本题可根据平移的性质，先确定$A$、$B$、$C$三点平移后的对应点$D$、$E$、$F$的位置，再顺次连接各点得到$\triangle DEF$。
已知将$\triangle ABC$向右平移$2$个单位，再向下平移$3$个单位，根据平移规律“右加左减，上加下减”，对于点$(x,y)$，向右平移$2$个单位后坐标变为$(x + 2,y)$，再向下平移$3$个单位后坐标变为$(x + 2,y - 3)$。
通过观察网格图，确定$A$、$B$、$C$三点的坐标，然后根据上述平移规律得到$D$、$E$、$F$三点的坐标，最后在网格中画出$\triangle DEF$。
（2）本题可根据三角形高的定义，利用网格的特点来画出$AC$边上的高$BH$。
三角形的高是从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高。
观察网格图，可利用网格的垂直关系，通过构造直角来画出$AC$边上的高$BH$。
【答案】：
(1)
图略（在网格中找到$A$、$B$、$C$三点向右平移$2$个单位，再向下平移$3$个单位后的对应点$D$、$E$、$F$，然后顺次连接$D$、$E$、$F$得到$\triangle DEF$）
(2)
图略（利用网格的垂直关系，过点$B$作$AC$的垂线，垂足为$H$，$BH$即为$AC$边上的高）