第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 一个三角形三个内角的度数之比是$ 1:2:3 $,这个三角形是 (
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
答案:
B
9. [2025年1月合肥期末]将一副三角板($ ∠A = 30^{\circ} $)按如图所示的方式摆放,使得$ AB// EF $,则∠1的度数为 (
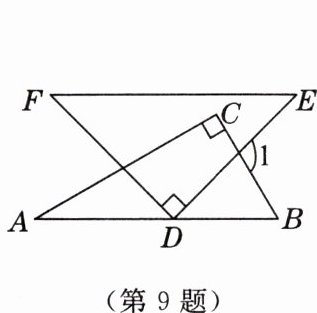
A.$ 75^{\circ} $
B.$ 90^{\circ} $
C.$ 105^{\circ} $
D.$ 115^{\circ} $
C
)
A.$ 75^{\circ} $
B.$ 90^{\circ} $
C.$ 105^{\circ} $
D.$ 115^{\circ} $
答案:
C
10. 如图,已知$ ∠A + ∠B + ∠C = 125^{\circ} $,则$ ∠D + ∠E = $
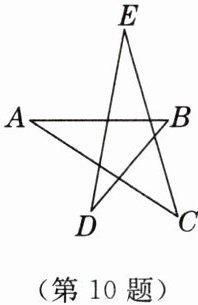
55
$ ^{\circ} $.
答案:
55
11. 如图,在△ABD中,$ ∠ABD = ∠BAD = 2∠D $,AC是∠BAD的平分线,交边AD上的高BE于点F.
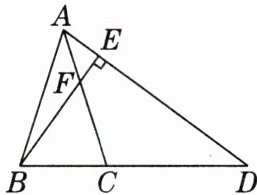
(1)求∠ABE的度数;
(2)求∠BFC的度数.

(1)求∠ABE的度数;
(2)求∠BFC的度数.
答案:
解:
(1)∠ABE=18°.
(2)∠BFC=54°.
(1)∠ABE=18°.
(2)∠BFC=54°.
12. 整体思想 如图,在△ABC中,$ ∠EFD = 30^{\circ} $,且$ ∠AEF = ∠AFE $,$ ∠CFD = ∠CDF $,则∠ABC的度数为 (
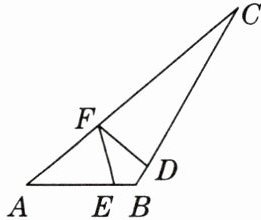
A.$ 90^{\circ} $
B.$ 110^{\circ} $
C.$ 120^{\circ} $
D.$ 150^{\circ} $
C
)
A.$ 90^{\circ} $
B.$ 110^{\circ} $
C.$ 120^{\circ} $
D.$ 150^{\circ} $
答案:
C
13. 分类讨论思想 如图,已知$ ∠AOD = 30^{\circ} $,C是射线OD上的一个动点,在点C的运动过程中,当△AOC恰好是直角三角形时,∠ACO的度数为
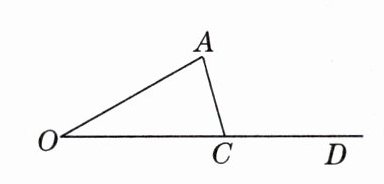
90°或60°
.
答案:
90°或60°
14. 在△ABC中,$ AB = AC $,且AC上的中线BD把这个三角形的周长分成了12和6两部分,则这个三角形的腰长和底边长分别为
8,2
.
答案:
8,2
15. [2024·合肥三模]如图是某款婴儿手推车的平面示意图,若$ AB// CD $,$ ∠1 = 130^{\circ} $,$ ∠3 = 35^{\circ} $,则∠2的度数为 (
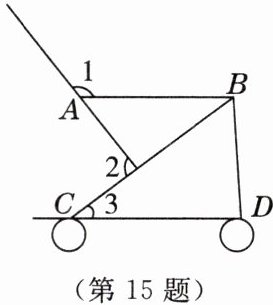
A.$ 75^{\circ} $
B.$ 80^{\circ} $
C.$ 85^{\circ} $
D.$ 90^{\circ} $
C
)
A.$ 75^{\circ} $
B.$ 80^{\circ} $
C.$ 85^{\circ} $
D.$ 90^{\circ} $
答案:
C
16. [2023·安徽中考]清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论:如图,AD是锐角三角形ABC的高,则$ BD = \frac{1}{2}(BC + \frac{AB^{2} - AC^{2}}{BC}) $.当$ AB = 7 $,$ BC = 6 $,$ AC = 5 $时,$ CD = $
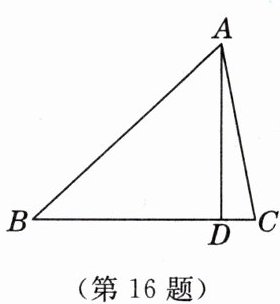
1
.
答案:
1
查看更多完整答案,请扫码查看


