《2025年点拨训练八年级数学上册沪科版安徽专版》

1. [2025年1月南京期末节选]【问题背景】若一个函数,对于自变量的不同取值范围,该函数有不同的表达式,则这样的函数称为“分段函数”.
当$x\geqslant 0$时,$y_{1}= kx + 2$；
当$x ＜ 0$时,$y_{1}= kx - 2$,
可以记作分段函数$y_{1}= \left\{\begin{array}{l}kx + 2(x\geqslant 0),\\kx - 2(x ＜ 0).\end{array} \right.$
【问题探究】当$k = 1$时,画出$y_{1}与x$之间的函数图象,并写出该函数两条不同类型的性质.

答案： 解：当k=1时，y₁=｛x+2(x≥0)，
x-2(x＜0)，
画图略.
性质1:当x≥0时，y随x的增大而增大；
性质2:当x≥0时，函数有最小值2.(性质不唯一)

2. [2025年1月广州期末]某市出租车白天的收费起步价为12元,即路程不超过3km时收费12元,超过部分每千米收费2.6元.如果乘客白天乘坐出租车的路程为$x$km,乘车费为$y$元,那么$y与x$之间的关系式为y=｛12(x≤3)，2.6x+4.2(x＞3).

答案： y=｛12(x≤3)，
2.6x+4.2(x＞3)

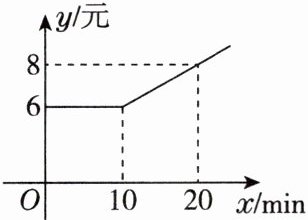
3. [2025年1月武汉期末]共享电动车是一种新理念下的交通工具,主要面向3～10km的出行市场,图中反映某共享电动车平台收费$y$(元)与骑行时间$x$(min)之间的函数关系,根据图中的信息,某天小明从家到学校一共骑行40min,则需要向平台付费12元.

答案： 12

4. 随着新能源汽车的普及,充电站如雨后春笋般出现.某充电站施行峰谷电价收费制度(高峰时段：10：00至22：00,低谷时段：22：00至次日10：00),已知高峰时段的充电单价是低谷时段的2倍,且充电总费用$y$(元)与充电量$x$(千瓦时)之间成一次函数关系,下图为一辆新能源汽车从充电开始直至充电结束的整个计费过程.
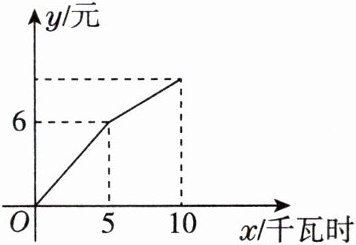
(1)求出当$0\leqslant x\leqslant 5$时,充电总费用$y$(元)与充电量$x$(千瓦时)之间的函数表达式；
(2)当这辆汽车充电结束时,充电总费用是多少？
(3)当充电总费用为7.8元时,充电量为8千瓦时.

解：
(1)设充电总费用y(元)与充电量x(千瓦时)之间的函数表达式为y=kx，
将(5,6)代入，得6=5k，解得k=1.2，所以y=1.2x.
(2)因为高峰时段的充电单价是低谷时段充电单价的2倍，所以低谷时段的充电单价为1.2÷2=0.6(元/千瓦时)，1.2×5+0.6×(10-5)=6+3=9.
答：当这辆汽车充电结束时，充电总费用是9元.
(3)8

答案： 解：
(1)设充电总费用y(元)与充电量x(千瓦时)之间的函数表达式为y=kx，
将(5,6)代入，得6=5k，解得k=1.2，所以y=1.2x.
(2)因为高峰时段的充电单价是低谷时段充电单价的2倍，所以低谷时段的充电单价为1.2÷2=0.6(元/千瓦时)，1.2×5+0.6×(10-5)=6+3=9.
答：当这辆汽车充电结束时，充电总费用是9元.
(3)8