第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 从已知条件出发,依据
2. 证明与图形有关的命题时,一般有以下步骤:
第一步:根据题意,画出图形;
第二步:写出已知、求证;
第三步:分析题意,找出证明途径;
第四步:写出证明过程.
定义
、基本事实、定理,并按照逻辑规则,推导出结论,这一方法称为演绎推理(或演绎法). 演绎推理的过程,就是演绎证明,简称证明.2. 证明与图形有关的命题时,一般有以下步骤:
第一步:根据题意,画出图形;
第二步:写出已知、求证;
第三步:分析题意,找出证明途径;
第四步:写出证明过程.
答案:
1.定义
1. 两点确定一条直线是(
A.定义
B.基本事实
C.定理
D.假命题
B
)A.定义
B.基本事实
C.定理
D.假命题
答案:
1.B
2. 创新题·开放题 请写出一个关于角相等的定理:
两直线平行,同位角相等(答案不唯一)
.
答案:
2.两直线平行,同位角相等(答案不唯一)
3. 下列说法中,错误的是
①所有的定义都是命题;②所有的基本事实都是命题;③所有的定理都是命题;④所有的命题都是定理.
④
. (填序号)①所有的定义都是命题;②所有的基本事实都是命题;③所有的定理都是命题;④所有的命题都是定理.
答案:
3.④
4. 教材改编题 如图,若$AO\perp CO$,$BO\perp DO$,则$\angle AOB= \angle COD$,推理的依据是(
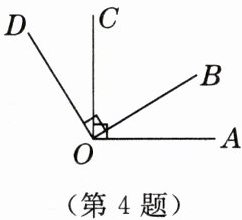
A.同角的补角相等
B.同角的余角相等
C.对顶角相等
D.垂直的定义
B
)
A.同角的补角相等
B.同角的余角相等
C.对顶角相等
D.垂直的定义
答案:
4.B
5. [2025·滁州月考] 补全下面的证明过程,并填上推理的依据.
已知:如图,点$F在线段AD$上,点$B$,$C$,$E$共线,$\angle B+\angle BCD= 180^{\circ}$,$\angle B= \angle D$.
求证:$\angle E= \angle DFE$.
证明:$\because\angle B+\angle BCD= 180^{\circ}$(已知),
$\therefore AB// CD$(
$\therefore\angle B= $
又$\because\angle B= \angle D$(已知),
$\therefore$
$\therefore AD// BE$(
$\therefore\angle E= \angle DFE$(
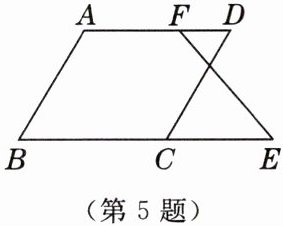
已知:如图,点$F在线段AD$上,点$B$,$C$,$E$共线,$\angle B+\angle BCD= 180^{\circ}$,$\angle B= \angle D$.
求证:$\angle E= \angle DFE$.
证明:$\because\angle B+\angle BCD= 180^{\circ}$(已知),
$\therefore AB// CD$(
同旁内角互补,两直线平行
),$\therefore\angle B= $
$\angle DCE$
(两直线平行,同位角相等
).又$\because\angle B= \angle D$(已知),
$\therefore$
$\angle DCE$
$=$$\angle D$
(等量代换
),$\therefore AD// BE$(
内错角相等,两直线平行
),$\therefore\angle E= \angle DFE$(
两直线平行,内错角相等
).
答案:
5.同旁内角互补,两直线平行;∠DCE;两直线平行,同位角相等;∠DCE;∠D;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
6. 下列命题中,是定理的是(
A.一个能被$2整除的数也必能被4$整除
B.相等的角是对顶角
C.同位角相等
D.三角形的内角和等于$180^{\circ}$
D
)A.一个能被$2整除的数也必能被4$整除
B.相等的角是对顶角
C.同位角相等
D.三角形的内角和等于$180^{\circ}$
答案:
6.D
7. [2025年1月合肥期末] 如图,已知下列三个条件:①$\angle 1+\angle 2= 180^{\circ}$,②$\angle 3= \angle A$,③$\angle B= \angle C$. 从中选出两个作为题设,其余一个作为结论,可以组成$3$个命题. 请从中选择一个真命题,写出已知和求证,并证明.
已知:
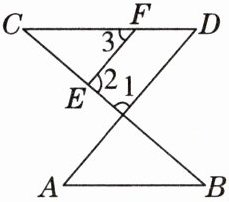
已知:
①②
. 求证:______③
. (填序号)
答案:
7.(答案不唯一)①②;③ 证明:
∵∠1+∠2=180°,
∴AD//EF,
∴∠3=∠D.
∵∠3=∠A,
∴∠A=∠D,
∴AB//CD,
∴∠B=∠C.
∵∠1+∠2=180°,
∴AD//EF,
∴∠3=∠D.
∵∠3=∠A,
∴∠A=∠D,
∴AB//CD,
∴∠B=∠C.
查看更多完整答案,请扫码查看


