第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9. 创新题·新考法如图,把四盏相同的灯笼放置在平面直角坐标系中,坐标分别是$A(-3.5,b)$,$B(-2,b)$,$C(-1,b)$,$D(1,b)$,将其中一盏灯笼向右平移$m$个单位长度,使得$y$轴两侧的灯笼对称,则$m$的值可以是(
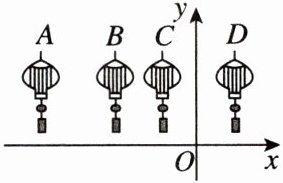
A.3
B.4
C.4.5
D.5.5
D
)
A.3
B.4
C.4.5
D.5.5
答案:
D
10. [2025·重庆期中]如图,在平面直角坐标系中,对$\triangle ABC$进行循环往复的轴对称变换,若原来点$B的坐标是(-5,2)$,则经过第2025次变换后点$B$的对应点的坐标为(
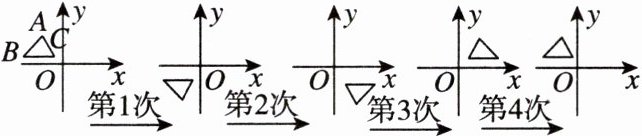
A.$(5,2)$
B.$(5,-2)$
C.$(-5,-2)$
D.$(-5,2)$
C
)
A.$(5,2)$
B.$(5,-2)$
C.$(-5,-2)$
D.$(-5,2)$
答案:
C
11. 如图,在平面直角坐标系中,$\triangle PQR的三个顶点分别为P(-1,3)$,$Q(-4,5)$,$R(-4,1)$,直线$m$上各点的横坐标都为1,直线$n$上各点的纵坐标都为-1。
(1)在图中分别作出$\triangle PQR关于直线m和直线n$对称的图形。
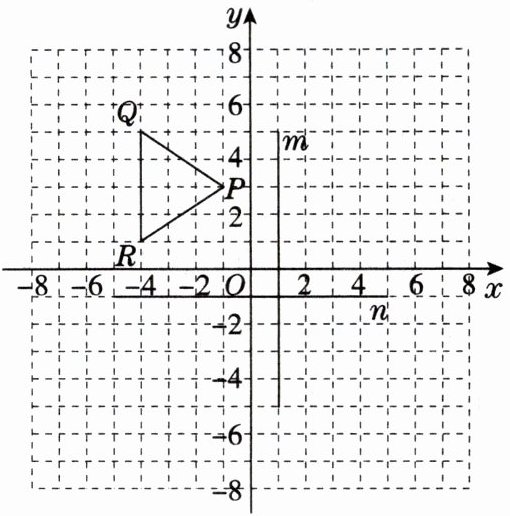
(2)填空:
①点$(x,y)关于直线m$对称的点的坐标为
②点$(x,y)关于直线n$对称的点的坐标为
(1)在图中分别作出$\triangle PQR关于直线m和直线n$对称的图形。

(2)填空:
①点$(x,y)关于直线m$对称的点的坐标为
$(2-x,y)$
;②点$(x,y)关于直线n$对称的点的坐标为
$(x,-2-y)$
。
答案:
11.解:
(1)略.
(2)①$(2-x,y)$ ②$(x,-2-y)$
(1)略.
(2)①$(2-x,y)$ ②$(x,-2-y)$
即时练透/与轴对称有关的最短路径问题/
思维可视化如图,$A$,$B$两个城市需要从临近的一条河流引入水源,通过数学方法,建立了平面直角坐标系,单位长度为$1km$,$x$轴为河流,城市$A的坐标为(0,2)$,城市$B的坐标为(4,1)$,现在要在$x$轴(河流)上建造一座供水站$P分别向城市A$、$B$供水,使得输水管道总长度$PA+PB$最小,如何求$P$的坐标?
思维过程
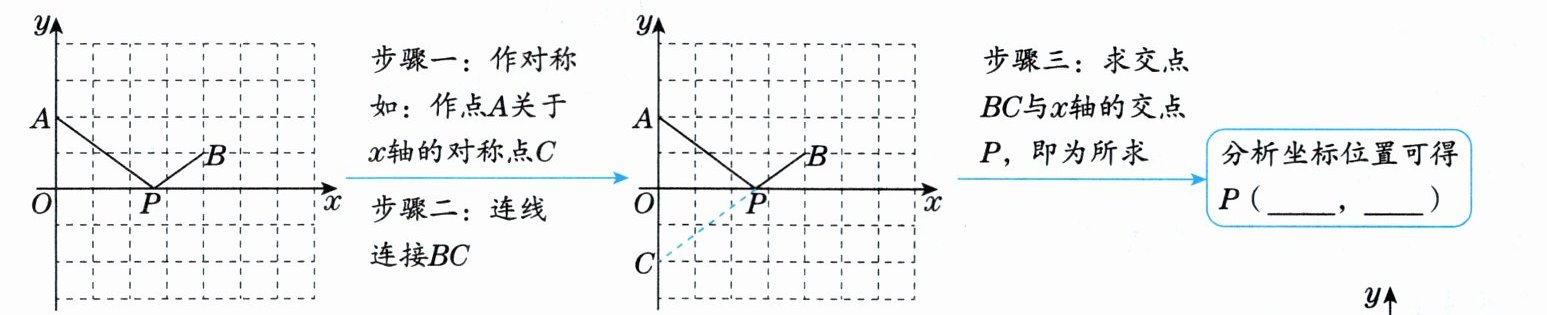
思维可视化如图,$A$,$B$两个城市需要从临近的一条河流引入水源,通过数学方法,建立了平面直角坐标系,单位长度为$1km$,$x$轴为河流,城市$A的坐标为(0,2)$,城市$B的坐标为(4,1)$,现在要在$x$轴(河流)上建造一座供水站$P分别向城市A$、$B$供水,使得输水管道总长度$PA+PB$最小,如何求$P$的坐标?
思维过程

答案:
【解析】:本题主要考查平面直角坐标系中的轴对称性质以及最短路径问题。首先,找到点$A$关于$x$轴的对称点$A'$。由于$A$的坐标为$(0,2)$,所以$A'$的坐标为$(0, -2)$。接着,连接点$A'$和$B$,该连线与$x$轴的交点即为所求的$P$点。这是因为根据轴对称性质,$PA = PA'$,所以$PA + PB = PA' + PB$,而$A'B$是连接$A'$和$B$的最短路径。设直线$A'B$的解析式为$y = kx + b$。将点$A'(0, -2)$和点$B(4, 1)$代入得到方程组:$\begin{cases}-2 = b \\1 = 4k + b\end{cases}$解这个方程组,得到:从第一个方程,我们直接得出$b = -2$。将$b = -2$代入第二个方程,得到:$1 = 4k - 2$$4k = 3$$k = \frac{3}{4}$因此,直线$A'B$的解析式为$y = \frac{3}{4}x - 2$。为了找到这条直线与$x$轴的交点,我们令$y = 0$并解出$x$的值:$\frac{3}{4}x - 2 = 0$$\frac{3}{4}x = 2$$x = \frac{8}{3}$所以,交点$P$的坐标为$\left(\frac{8}{3}, 0\right)$。【答案】:$P\left(\frac{8}{3},0\right)$。
针对练习
如图,在平面直角坐标系中,点$A$,$B$,$C的坐标分别为A(1,-2)$,$B(3,2)$,$C(-3,2)$,点$D在y$轴上运动,当$\triangle ABD$的周长最小时,点$D$的坐标为
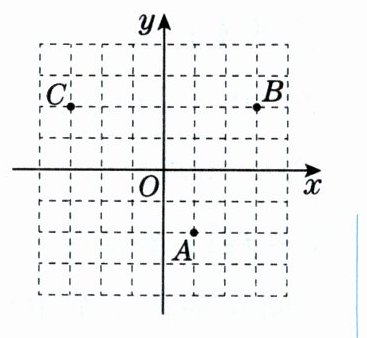
如图,在平面直角坐标系中,点$A$,$B$,$C的坐标分别为A(1,-2)$,$B(3,2)$,$C(-3,2)$,点$D在y$轴上运动,当$\triangle ABD$的周长最小时,点$D$的坐标为
$(0,-1)$
。
答案:
$(0,-1)$
查看更多完整答案,请扫码查看


