第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 由三角形的一边与另一边的
延长线
组成的角,叫作三角形的外角. 三角形的每个顶点处都有2个外角,它们是对顶角.
答案:
延长线
2.

答案:
等于;大于;360°
1. 如图,在$\angle 1$,$\angle 2$,$\angle 3$中,是$\triangle ABC$外角的是(
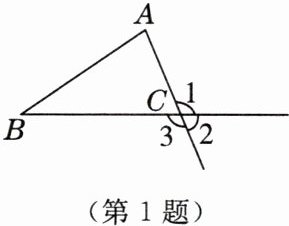
A.$\angle 1$
B.$\angle 2$,$\angle 3$
C.$\angle 1$,$\angle 3$
D.$\angle 1$,$\angle 2$,$\angle 3$
C
)
A.$\angle 1$
B.$\angle 2$,$\angle 3$
C.$\angle 1$,$\angle 3$
D.$\angle 1$,$\angle 2$,$\angle 3$
答案:
C
2. 下列说法中错误的是
①一个三角形只有三个外角;
②三角形的每个顶点处都有两个外角;
③三角形的每个外角是与它相邻内角的邻补角;
④一个三角形共有六个外角.
①
.(填序号)①一个三角形只有三个外角;
②三角形的每个顶点处都有两个外角;
③三角形的每个外角是与它相邻内角的邻补角;
④一个三角形共有六个外角.
答案:
①
3. [2025年1月厦门期末]如图,在$\triangle ABC$中,$\angle A= 35^{\circ}$,$\angle B= 25^{\circ}$,则$\angle ACD$的度数是(
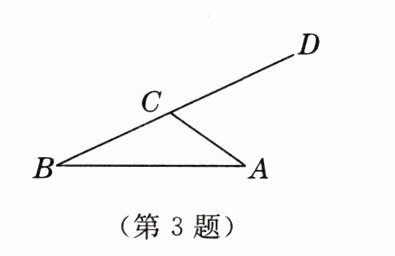
A.$60^{\circ}$
B.$55^{\circ}$
C.$120^{\circ}$
D.$65^{\circ}$
A
)
A.$60^{\circ}$
B.$55^{\circ}$
C.$120^{\circ}$
D.$65^{\circ}$
答案:
A
4. 跨学科·体育 体育课上的侧压腿动作可以抽象为几何图形(如图),若$\angle 1= 110^{\circ}$,则$\angle 2$等于(
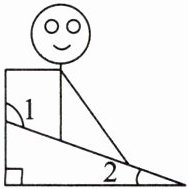
A.$10^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
B
)
A.$10^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
答案:
B
5. 如图,$\angle 1$,$\angle 2$,$\angle 3$的大小关系为
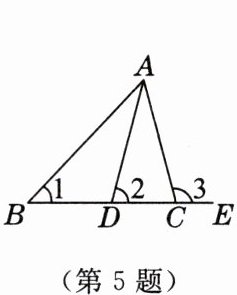
$\angle 3>\angle 2>\angle 1$
.
答案:
【解析】:本题考查三角形外角的性质,即三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABD$中,$\angle 2$是外角,所以$\angle 2>\angle 1$。
在$\triangle ACD$中,$\angle 3$是外角,所以$\angle 3>\angle 2$。
综上可得$\angle 3>\angle 2>\angle 1$。
【答案】:$\angle 3>\angle 2>\angle 1$
在$\triangle ABD$中,$\angle 2$是外角,所以$\angle 2>\angle 1$。
在$\triangle ACD$中,$\angle 3$是外角,所以$\angle 3>\angle 2$。
综上可得$\angle 3>\angle 2>\angle 1$。
【答案】:$\angle 3>\angle 2>\angle 1$
6. 如图,$\angle A= 20^{\circ}$,$\angle B= 30^{\circ}$,$\angle C= 50^{\circ}$,则$\angle ADB$的度数为
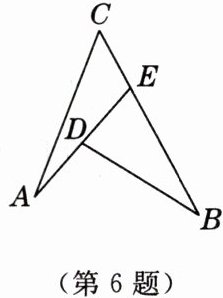
100°
.
答案:
100°
7. [2025年1月合肥期末]如图,$F是\triangle ABC的边BC$延长线上的一点,$DF\perp AB$,$\angle A= 30^{\circ}$,$\angle F= 40^{\circ}$,求$\angle ACF$的度数.
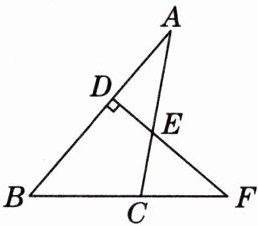

答案:
解:∠ACF=80°.
8. 已知一个三角形的三个外角的度数比为$2:3:4$,则它的最小的内角的度数为
$20°$
.
答案:
【解析】:
本题主要考查三角形的外角性质以及内外角关系。
首先,根据三角形的外角和性质,一个三角形的三个外角之和为$360^\circ$。
题目给出三个外角的度数比为$2:3:4$,因此可以设三个外角的度数分别为$2k^\circ$,$3k^\circ$,$4k^\circ$(其中$k$是一个正实数)。
根据外角和性质,有方程:
$2k + 3k + 4k = 360$
$9k = 360$
$k = 40$
将$k = 40$代入各外角的表达式,得到三个外角的度数分别为:
$2k^\circ = 80^\circ$
$3k^\circ = 120^\circ$
$4k^\circ = 160^\circ$
由于一个内角与其相邻的外角是互补的,即它们的度数之和为$180^\circ$,因此,三角形的三个内角的度数分别为:
$180^\circ - 80^\circ = 100^\circ$(但这不是最小的,所以先记下)
$180^\circ - 120^\circ = 60^\circ$
$180^\circ - 160^\circ = 20^\circ$(这是最小的内角)
从上面的计算中,可以看出最小的内角是$20^\circ$。
【答案】:
$20^\circ$
本题主要考查三角形的外角性质以及内外角关系。
首先,根据三角形的外角和性质,一个三角形的三个外角之和为$360^\circ$。
题目给出三个外角的度数比为$2:3:4$,因此可以设三个外角的度数分别为$2k^\circ$,$3k^\circ$,$4k^\circ$(其中$k$是一个正实数)。
根据外角和性质,有方程:
$2k + 3k + 4k = 360$
$9k = 360$
$k = 40$
将$k = 40$代入各外角的表达式,得到三个外角的度数分别为:
$2k^\circ = 80^\circ$
$3k^\circ = 120^\circ$
$4k^\circ = 160^\circ$
由于一个内角与其相邻的外角是互补的,即它们的度数之和为$180^\circ$,因此,三角形的三个内角的度数分别为:
$180^\circ - 80^\circ = 100^\circ$(但这不是最小的,所以先记下)
$180^\circ - 120^\circ = 60^\circ$
$180^\circ - 160^\circ = 20^\circ$(这是最小的内角)
从上面的计算中,可以看出最小的内角是$20^\circ$。
【答案】:
$20^\circ$
9. 如图,$\angle BAE$,$\angle CBF$,$\angle ACD是\triangle ABC$的三个外角,$\angle ACD= 130^{\circ}$,则$\angle BAE+\angle CBF= $
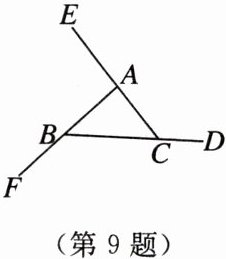
230
$^{\circ}$.
答案:
解:
∵∠ACD是△ABC的外角,
∴∠ACD = ∠BAC + ∠ABC = 130°。
∵∠BAE是∠BAC的邻补角,∠CBF是∠ABC的邻补角,
∴∠BAE = 180° - ∠BAC,∠CBF = 180° - ∠ABC。
∴∠BAE + ∠CBF = 180° - ∠BAC + 180° - ∠ABC = 360° - (∠BAC + ∠ABC) = 360° - 130° = 230°。
230
∵∠ACD是△ABC的外角,
∴∠ACD = ∠BAC + ∠ABC = 130°。
∵∠BAE是∠BAC的邻补角,∠CBF是∠ABC的邻补角,
∴∠BAE = 180° - ∠BAC,∠CBF = 180° - ∠ABC。
∴∠BAE + ∠CBF = 180° - ∠BAC + 180° - ∠ABC = 360° - (∠BAC + ∠ABC) = 360° - 130° = 230°。
230
10. [2024·芜湖期中]如图,在$\triangle ABC$中,沿虚线剪去$\angle C$,若$\angle 1+\angle 2= 240^{\circ}$,则$\angle C$的度数为
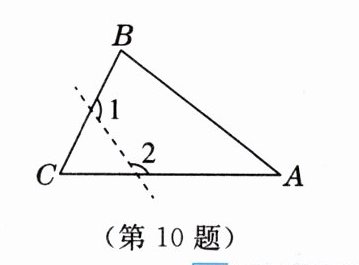
60°
.
答案:
解:在△ABC中,∠A+∠B+∠C=180°,则∠A+∠B=180°-∠C。
因为∠1、∠2是四边形ABDE的外角(假设剪去∠C后形成四边形ABDE,其中∠1和∠2是四边形的两个外角),四边形内角和为360°,所以∠A+∠B+∠1+∠2=360°。
已知∠1+∠2=240°,则∠A+∠B=360°-240°=120°。
又因为∠A+∠B=180°-∠C,所以180°-∠C=120°,解得∠C=60°。
60°
因为∠1、∠2是四边形ABDE的外角(假设剪去∠C后形成四边形ABDE,其中∠1和∠2是四边形的两个外角),四边形内角和为360°,所以∠A+∠B+∠1+∠2=360°。
已知∠1+∠2=240°,则∠A+∠B=360°-240°=120°。
又因为∠A+∠B=180°-∠C,所以180°-∠C=120°,解得∠C=60°。
60°
查看更多完整答案,请扫码查看


