第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. 立德树人·关注生活如图,有三条公路两两相交,要选择一地点建一座加油站,若要使加油站到三条公路的距离相等,则满足此要求的加油站的位置有(
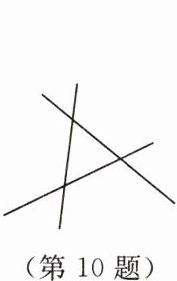
A.1个
B.2个
C.3个
D.4个
D
)
A.1个
B.2个
C.3个
D.4个
答案:
D
11. [2025·温州模拟]如图,△ABC中,∠C= 90°,BC= 6,AC= 8,AB= 10,以点B为圆心,适当长为半径画弧,分别交AB,BC于点M,N,再分别以点M和点N为圆心,大于$\frac{1}{2}MN$的长为半径作弧(弧所在圆的半径都相等),两弧交于点E,画射线BE交AC于点D,则线段CD的长为(
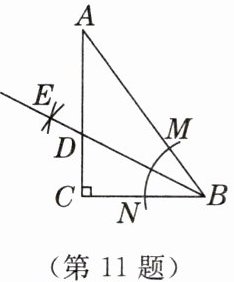
A.2
B.3
C.5
D.6
B
)
A.2
B.3
C.5
D.6
答案:
B
12. 如图,△ABC的三边AB,AC,BC的长分别为4,6,8,点O是三条角平分线的交点,将△ABC分成三个三角形,则$S_{△OAB}:S_{△OAC}:S_{△OBC}=$
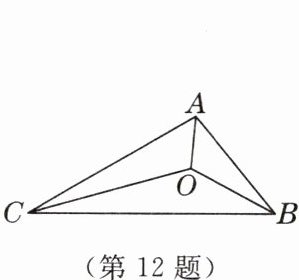
2:3:4
.
答案:
2:3:4
13. [2025·广州期中]如图,已知∠B= ∠C= 90°,M是BC的中点,DM平分∠ADC,∠CMD= 35°,则∠MAB的度数是
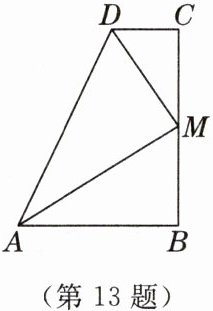
35°
.
答案:
35°
14. [2025年1月大兴期末]如图,OC是∠AOB的平分线,点D,P分别在射线OC和OB上,OD>DP且∠DPO= 36°,点Q是射线OA上的一点,若DQ= DP,则∠DQO的度数为
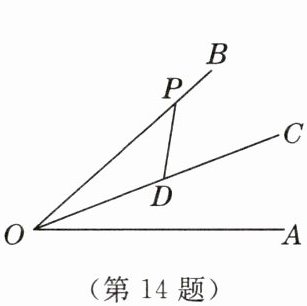
36°或144°
.
答案:
36°或144°
15. 如图,某城市公园里有两个景点B,C,直线$l_1,l_3$表示直路,而$l_2$表示弯路.想在S区里修建一座公厕P,使它到两条路$l_1$和$l_3$的距离相等,且到两个景点B和C的距离也相等.请在图中标出点P的位置.(用尺规作图,保留作图痕迹)
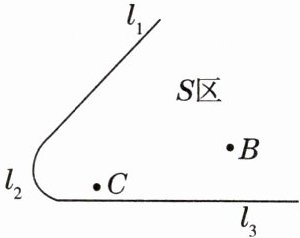

答案:
【解析】:本题主要考查角平分线和线段垂直平分线的尺规作图。
角平分线的性质是角平分线上的点到角两边的距离相等,所以到两条路$l_1$和$l_3$距离相等的点在$l_1$与$l_3$夹角的平分线上;
线段垂直平分线的性质是线段垂直平分线上的点到线段两端的距离相等,所以到两个景点$B$和$C$距离相等的点在线段$BC$的垂直平分线上。
因此,点$P$是$l_1$与$l_3$夹角的平分线和线段$BC$垂直平分线的交点。
尺规作图步骤如下:
以$l_1$与$l_3$的交点为圆心,任意长为半径画弧,分别交$l_1$、$l_3$于两点,再分别以这两个交点为圆心,大于两交点距离一半的长为半径画弧,两弧在$l_1$与$l_3$夹角内部相交于一点,过这个交点和$l_1$与$l_3$的交点作射线,此射线即为$l_1$与$l_3$夹角的平分线。
分别以点$B$、$C$为圆心,大于$\frac{1}{2}BC$的长为半径画弧,两弧分别相交于两点,过这两个交点作直线,此直线即为线段$BC$的垂直平分线。
$l_1$与$l_3$夹角的平分线和线段$BC$垂直平分线的交点即为点$P$的位置。
【答案】:图略(按照上述尺规作图步骤作出$l_1$与$l_3$夹角的平分线和线段$BC$的垂直平分线,它们的交点即为点$P$)。
角平分线的性质是角平分线上的点到角两边的距离相等,所以到两条路$l_1$和$l_3$距离相等的点在$l_1$与$l_3$夹角的平分线上;
线段垂直平分线的性质是线段垂直平分线上的点到线段两端的距离相等,所以到两个景点$B$和$C$距离相等的点在线段$BC$的垂直平分线上。
因此,点$P$是$l_1$与$l_3$夹角的平分线和线段$BC$垂直平分线的交点。
尺规作图步骤如下:
以$l_1$与$l_3$的交点为圆心,任意长为半径画弧,分别交$l_1$、$l_3$于两点,再分别以这两个交点为圆心,大于两交点距离一半的长为半径画弧,两弧在$l_1$与$l_3$夹角内部相交于一点,过这个交点和$l_1$与$l_3$的交点作射线,此射线即为$l_1$与$l_3$夹角的平分线。
分别以点$B$、$C$为圆心,大于$\frac{1}{2}BC$的长为半径画弧,两弧分别相交于两点,过这两个交点作直线,此直线即为线段$BC$的垂直平分线。
$l_1$与$l_3$夹角的平分线和线段$BC$垂直平分线的交点即为点$P$的位置。
【答案】:图略(按照上述尺规作图步骤作出$l_1$与$l_3$夹角的平分线和线段$BC$的垂直平分线,它们的交点即为点$P$)。
16. [2025年1月芜湖期末]如图,在△ABC中,∠BAC= 120°,BE,CF是△ABC的角平分线,它们相交于点I.
(1)如图①,连接AI,求证:点I在∠BAC的平分线上;
(2)如图②,延长AI交BC于点D,过点F作FT⊥BC于点T,FL⊥AD于点L.求证:FT= FL.
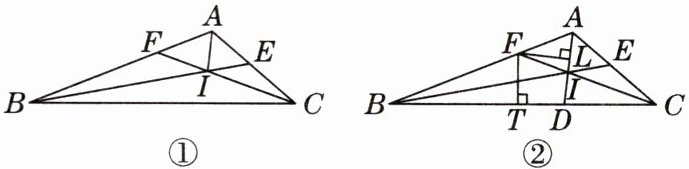
(1)如图①,连接AI,求证:点I在∠BAC的平分线上;
(2)如图②,延长AI交BC于点D,过点F作FT⊥BC于点T,FL⊥AD于点L.求证:FT= FL.

答案:
证明:
(1)如图①,过点I作AB,AC,BC的垂线段,分别交于点M,N,K.
∵BE,CF是△ABC的角平分线,
∴IK=IM,IK=IN,
∴IN=IM,
∴点I在∠BAC 的角平分线上.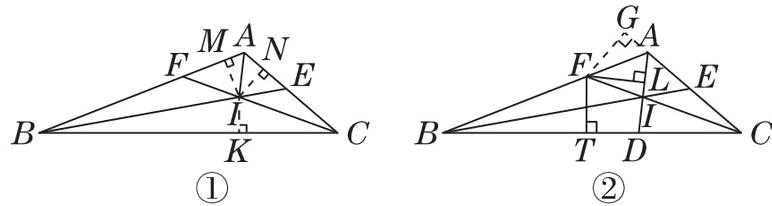
(2)如图②,过点F作AC的垂线段,交CA的延长线于点G,
∵CF是△ABC的角平分线,FT⊥BC,FG⊥CA,
∴FT=FG.
∵∠BAC=120°,
∴∠GAF=180°−∠BAC=60°.
∵AD是∠BAC的平分线,
∴∠BAD= $\frac{1}{2}$∠BAC= $\frac{1}{2}$×120°=60°,
∴∠BAD=∠GAF,
∵FG⊥AG,FL⊥AD,
∴FL=FG,
∴FT=FL.
证明:
(1)如图①,过点I作AB,AC,BC的垂线段,分别交于点M,N,K.
∵BE,CF是△ABC的角平分线,
∴IK=IM,IK=IN,
∴IN=IM,
∴点I在∠BAC 的角平分线上.

(2)如图②,过点F作AC的垂线段,交CA的延长线于点G,
∵CF是△ABC的角平分线,FT⊥BC,FG⊥CA,
∴FT=FG.
∵∠BAC=120°,
∴∠GAF=180°−∠BAC=60°.
∵AD是∠BAC的平分线,
∴∠BAD= $\frac{1}{2}$∠BAC= $\frac{1}{2}$×120°=60°,
∴∠BAD=∠GAF,
∵FG⊥AG,FL⊥AD,
∴FL=FG,
∴FT=FL.
查看更多完整答案,请扫码查看


