《2025年点拨训练八年级数学上册沪科版安徽专版》

两角分别相等且其中一组等角的对边相等的两个三角形全等.简记为“角角边”或“AAS”.
1星题 基础题

答案： 对边

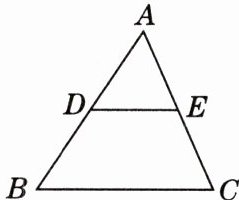
1. 原创题 如图,在△ABC中,D是AB上任意一点,若DE//BC交AC于点E,则△ADE与△ABC的三个角分别相等,显然这两个三角形不全等,这说明当两个三角形满足三角分别相等时,两个三角形不一定全等.

答案： 三角分别相等

2. 根据下列已知条件,不能画出唯一△ABC的是(B)
A.AB= 10,BC= 6,CA= 5
B.AB= 10,BC= 6,∠A= 30°
C.AB= 10,BC= 6,∠B= 60°
D.∠A= 60°,AB= 4,∠B= 45°

答案： B

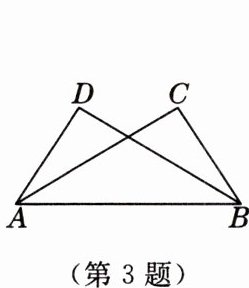
3. [知识初练]如图,∠C= ∠D,∠ABC= ∠BAD,要证明△ABC≌△BAD,可直接使用全等三角形的判定定理(C)

A.SSS
B.SAS
C.AAS
D.ASA

答案： C

4. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且BE= CD,∠B= ∠C,AD= 4,CE= 5,则AB= 9.

答案： 9

5. [2025·滁州模拟]如图,AC= AD,AD//BC,∠B+∠CED= 180°,求证：△ABC≌△DEA.

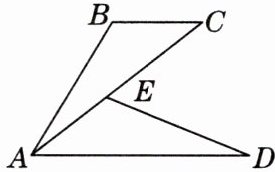
答案： 证明：
∵AD//BC，
∴∠B=∠DAE（两直线平行，同位角相等）。
∵∠B+∠CED=180°，∠DEA+∠CED=180°（平角定义），
∴∠B=∠DEA（同角的补角相等），
∴∠DAE=∠DEA（等量代换），
∴AE=AD（等角对等边）。
∵AC=AD，
∴AC=AE（等量代换）。
在△ABC和△DEA中，
$\left\{\begin{array}{l} ∠B=∠DEA,\\ ∠BAC=∠EDA,\\ AC=EA,\end{array}\right.$
∴△ABC≌△DEA（AAS）。

6. 跨学科·物理 如图,在一个支架的横杆上点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,OA表示小球静止时的位置.当小华用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D；当小球摆到OC位置时,OB与OC恰好垂直(图中的点A,B,O,C在同一平面上),过点C作CE⊥OA于点E.已知CE= 13cm,细绳OA的长为15cm,求AD的长.

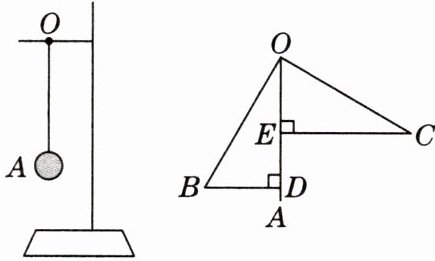
答案： 解：AD=2 cm.