第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9.[2024.广州期末]下列长度的三条线段不能组成三角形的是 (
A.2.5,3,5
B.7,6,12
C.a-3,a,3(a>3)
D.a,a+4,a+6(a>2)
C
)A.2.5,3,5
B.7,6,12
C.a-3,a,3(a>3)
D.a,a+4,a+6(a>2)
答案:
解:A. 2.5+3=5.5>5,3+5=8>2.5,2.5+5=7.5>3,能组成三角形。
B. 7+6=13>12,6+12=18>7,7+12=19>6,能组成三角形。
C. 因为a>3,所以a-3>0,a-3+3=a,不满足两边之和大于第三边,不能组成三角形。
D. 因为a>2,所以a+a+4=2a+4>a+6(2a+4 - (a+6)=a-2>0),a+a+6=2a+6>a+4,a+4+a+6=2a+10>a,能组成三角形。
答案:C
B. 7+6=13>12,6+12=18>7,7+12=19>6,能组成三角形。
C. 因为a>3,所以a-3>0,a-3+3=a,不满足两边之和大于第三边,不能组成三角形。
D. 因为a>2,所以a+a+4=2a+4>a+6(2a+4 - (a+6)=a-2>0),a+a+6=2a+6>a+4,a+4+a+6=2a+10>a,能组成三角形。
答案:C
10.20新月论期末如图,用AB,BC,CD,AD四条钢条固定成一个铁框,相邻两钢条的夹角均可调整,不计螺丝大小及重叠部分,若AB= 5,BC= 9,CD= 7,AD= 6,则所固定成的铁框中,两个顶点的距离最大值是(
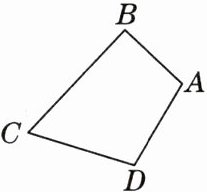
A.14
B.16
C.13
D.11
C
)
A.14
B.16
C.13
D.11
答案:
C
11.[2025年1月合肥期末]若α,b,c是△ABC的三边长,则化简|a十b-c|-|b-c-a|的结果是
2b - 2c
.
答案:
【解析】:
本题主要考查三角形中三边关系以及绝对值的化简。
在任意三角形ABC中,根据三角形的性质,任意两边之和大于第三边,任意两边之差小于第三边。
所以,对于边长a,b,c,我们有:
$a + b > c$
$b + c > a$
$c + a > b$
同时,也得到以下关系:
$|a + b - c| = a + b - c$ (因为 $a + b > c$)
对于 $|b - c - a|$,因为 $b < a + c$,所以 $b - c - a < 0$,那么:
$|b - c - a| = -(b - c - a) = c + a - b$
将上述两个结果代入原式,得到:
$|a + b - c| - |b - c - a| = (a + b - c) - (c + a - b) = 2b - 2c$
【答案】:
$2b - 2c$
本题主要考查三角形中三边关系以及绝对值的化简。
在任意三角形ABC中,根据三角形的性质,任意两边之和大于第三边,任意两边之差小于第三边。
所以,对于边长a,b,c,我们有:
$a + b > c$
$b + c > a$
$c + a > b$
同时,也得到以下关系:
$|a + b - c| = a + b - c$ (因为 $a + b > c$)
对于 $|b - c - a|$,因为 $b < a + c$,所以 $b - c - a < 0$,那么:
$|b - c - a| = -(b - c - a) = c + a - b$
将上述两个结果代入原式,得到:
$|a + b - c| - |b - c - a| = (a + b - c) - (c + a - b) = 2b - 2c$
【答案】:
$2b - 2c$
12.已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足$(a-b)^2+(b-c)^2= 0,$试判断
△ABC的形状;
(2)若△ABC的周长为12,a= 2,且△ABC是等
腰三角形,求b,c的值.
(1)若a,b,c满足$(a-b)^2+(b-c)^2= 0,$试判断
△ABC的形状;
(2)若△ABC的周长为12,a= 2,且△ABC是等
腰三角形,求b,c的值.
答案:
【解析】:
(1)首先分析第一个问题,题目给出了$(a-b)^2+(b-c)^2= 0$,由于平方和只有在每一项都为0的情况下才能为0(因为平方数总是非负的),所以可以推断出$a-b=0$和$b-c=0$,即$a=b$和$b=c$,从而得出$a=b=c$,这说明$\bigtriangleup ABC$是等边三角形。
(2)对于第二个问题,题目给出了$\bigtriangleup ABC$的周长为12,一边长为2,且为等腰三角形。需要分两种情况讨论:
当$a$为腰长时,由于等腰三角形的两腰相等,所以有$b=2$或$c=2$,但这会导致底边长度为$12-2-2=8$。由于$2+2<8$,不满足三角形的三边关系(任意两边之和大于第三边),所以这种情况应舍去。
当$b$为腰长时,由于等腰三角形的两腰相等,得到$b=c$。根据周长公式,可以列出等式$2+b+c=12$,由于$b=c$,可以化简为$2+2b=12$,解得$b=5$,所以$c=5$。此时三边长为2,5,5,满足三角形的三边关系。
当$c$为腰长时,同理可以得到$c=b=5$,此时三边长为2,5,5,也满足三角形的三边关系。
综上所述,对于第二个问题,$b$和$c$的值都是5。
【答案】:
(1)$\bigtriangleup ABC$是等边三角形;
(2)$b=5,c=5$。
(1)首先分析第一个问题,题目给出了$(a-b)^2+(b-c)^2= 0$,由于平方和只有在每一项都为0的情况下才能为0(因为平方数总是非负的),所以可以推断出$a-b=0$和$b-c=0$,即$a=b$和$b=c$,从而得出$a=b=c$,这说明$\bigtriangleup ABC$是等边三角形。
(2)对于第二个问题,题目给出了$\bigtriangleup ABC$的周长为12,一边长为2,且为等腰三角形。需要分两种情况讨论:
当$a$为腰长时,由于等腰三角形的两腰相等,所以有$b=2$或$c=2$,但这会导致底边长度为$12-2-2=8$。由于$2+2<8$,不满足三角形的三边关系(任意两边之和大于第三边),所以这种情况应舍去。
当$b$为腰长时,由于等腰三角形的两腰相等,得到$b=c$。根据周长公式,可以列出等式$2+b+c=12$,由于$b=c$,可以化简为$2+2b=12$,解得$b=5$,所以$c=5$。此时三边长为2,5,5,满足三角形的三边关系。
当$c$为腰长时,同理可以得到$c=b=5$,此时三边长为2,5,5,也满足三角形的三边关系。
综上所述,对于第二个问题,$b$和$c$的值都是5。
【答案】:
(1)$\bigtriangleup ABC$是等边三角形;
(2)$b=5,c=5$。
13.推理能刀如图①,P是△ABC内部的一点,
连接BP并延长交AC于点D.
(1)试探究AB+BC+CA与2BD的大小关系;
(2)试探究AB+AC与PB+PC的大小关系;
(3)如图②,D,E是△ABC内部两点,试探究
AB+AC与BD十DE十CE的大小关系.
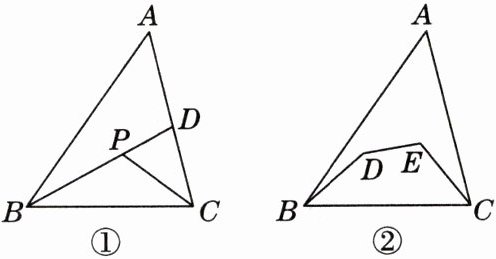
连接BP并延长交AC于点D.
(1)试探究AB+BC+CA与2BD的大小关系;
(2)试探究AB+AC与PB+PC的大小关系;
(3)如图②,D,E是△ABC内部两点,试探究
AB+AC与BD十DE十CE的大小关系.

答案:
【解析】:
本题可根据三角形三边关系“两边之和大于第三边”来探究各线段之间的大小关系。
(1)探究$AB + BC + CA$与$2BD$的大小关系
在$\triangle ABD$中,根据三角形三边关系可得$AB + AD\gt BD$ ①;
在$\triangle BCD$中,同理可得$BC + CD\gt BD$ ②;
将①+②可得:$AB + AD + BC + CD\gt 2BD$。
因为$AD + CD = AC$,所以$AB + BC + CA\gt 2BD$。
(2)探究$AB + AC$与$PB + PC$的大小关系
延长$BP$交$AC$于点$D$。
在$\triangle ABD$中,$AB + AD\gt BD$,即$AB + AD\gt PB + PD$ ③;
在$\triangle PCD$中,$PD + CD\gt PC$ ④;
将③+④可得:$AB + AD + PD + CD\gt PB + PD + PC$。
因为$AD + CD = AC$,两边同时减去$PD$,所以$AB + AC\gt PB + PC$。
(3)探究$AB + AC$与$BD + DE + CE$的大小关系
分别延长$BD$、$CE$交于点$F$,连接$AF$。
由(2)可知:
在$\triangle ABF$中,$AB + AF\gt BD + DF$ ⑤;
在$\triangle ADF$中,$AD + DF\gt DE + EF$ ⑥;
在$\triangle AEF$中,$AE + EF\gt CE$ ⑦;
将⑤+⑥+⑦可得:$AB + AF + AD + DF + AE + EF\gt BD + DF + DE + EF + CE$。
因为$AD + AE = AC$,两边同时减去$DF + EF$,所以$AB + AC\gt BD + DE + CE$。
【答案】:
(1)$AB + BC + CA\gt 2BD$;
(2)$AB + AC\gt PB + PC$;
(3)$AB + AC\gt BD + DE + CE$。
本题可根据三角形三边关系“两边之和大于第三边”来探究各线段之间的大小关系。
(1)探究$AB + BC + CA$与$2BD$的大小关系
在$\triangle ABD$中,根据三角形三边关系可得$AB + AD\gt BD$ ①;
在$\triangle BCD$中,同理可得$BC + CD\gt BD$ ②;
将①+②可得:$AB + AD + BC + CD\gt 2BD$。
因为$AD + CD = AC$,所以$AB + BC + CA\gt 2BD$。
(2)探究$AB + AC$与$PB + PC$的大小关系
延长$BP$交$AC$于点$D$。
在$\triangle ABD$中,$AB + AD\gt BD$,即$AB + AD\gt PB + PD$ ③;
在$\triangle PCD$中,$PD + CD\gt PC$ ④;
将③+④可得:$AB + AD + PD + CD\gt PB + PD + PC$。
因为$AD + CD = AC$,两边同时减去$PD$,所以$AB + AC\gt PB + PC$。
(3)探究$AB + AC$与$BD + DE + CE$的大小关系
分别延长$BD$、$CE$交于点$F$,连接$AF$。
由(2)可知:
在$\triangle ABF$中,$AB + AF\gt BD + DF$ ⑤;
在$\triangle ADF$中,$AD + DF\gt DE + EF$ ⑥;
在$\triangle AEF$中,$AE + EF\gt CE$ ⑦;
将⑤+⑥+⑦可得:$AB + AF + AD + DF + AE + EF\gt BD + DF + DE + EF + CE$。
因为$AD + AE = AC$,两边同时减去$DF + EF$,所以$AB + AC\gt BD + DE + CE$。
【答案】:
(1)$AB + BC + CA\gt 2BD$;
(2)$AB + AC\gt PB + PC$;
(3)$AB + AC\gt BD + DE + CE$。
查看更多完整答案,请扫码查看


