第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图,将四叶草放在平面直角坐标系中,其中落在第三象限的部分是(
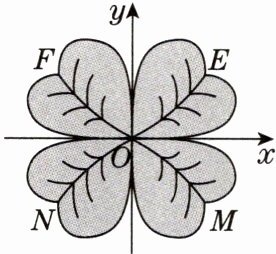
A.M
B.N
C.E
D.F
B
)
A.M
B.N
C.E
D.F
答案:
B
2. [2025·合肥月考]如图,在平面直角坐标系中有M,N,P,Q四个点,关于这四个点的坐标,下列描述正确的是(
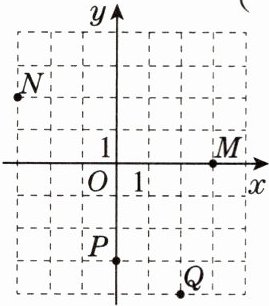
A.M的坐标为$(0,3)$
B.P的坐标为$(-3,0)$
C.N的坐标为$(-3,2)$
D.Q的坐标为$(-4,2)$
C
)
A.M的坐标为$(0,3)$
B.P的坐标为$(-3,0)$
C.N的坐标为$(-3,2)$
D.Q的坐标为$(-4,2)$
答案:
C
3. 点C在x轴的下方,y轴的右侧,距离x轴3个单位长度,距离y轴5个单位长度,则点C的坐标为(
A.$(-3,5)$
B.$(3,-5)$
C.$(5,-3)$
D.$(-5,3)$
(5, -3)
)A.$(-3,5)$
B.$(3,-5)$
C.$(5,-3)$
D.$(-5,3)$
答案:
【解析】:
首先,根据题目描述,点C在x轴的下方,这意味着其纵坐标应为负数。其次,点C在y轴的右侧,这意味着其横坐标应为正数。再根据题目给出的距离x轴3个单位长度和距离y轴5个单位长度,可以确定点C的横坐标为5,纵坐标为-3。因此,点C的坐标为$(5, -3)$。
【答案】:
C. $(5, -3)$
首先,根据题目描述,点C在x轴的下方,这意味着其纵坐标应为负数。其次,点C在y轴的右侧,这意味着其横坐标应为正数。再根据题目给出的距离x轴3个单位长度和距离y轴5个单位长度,可以确定点C的横坐标为5,纵坐标为-3。因此,点C的坐标为$(5, -3)$。
【答案】:
C. $(5, -3)$
4. [2025年1月马鞍山期末]若点$P(-a,b)$在第一象限,则点$Q(a,ab)$在第几象限?(
A.一
B.二
C.三
D.四
C
)A.一
B.二
C.三
D.四
答案:
【解析】:
首先,我们需要明确四个象限的坐标特点:
第一象限:横坐标和纵坐标都为正;
第二象限:横坐标为负,纵坐标为正;
第三象限:横坐标和纵坐标都为负;
第四象限:横坐标为正,纵坐标为负。
根据题意,点$P(-a,b)$在第一象限,那么它的横坐标$-a$为正,即$a$为负;同时,它的纵坐标$b$也为正。
接下来,我们要确定点$Q(a,ab)$的坐标特点。
由于已知$a$为负,$b$为正,那么$ab$为负(因为负数乘以正数得负数)。
所以,点$Q$的横坐标$a$为负,纵坐标$ab$也为负。
根据四个象限的坐标特点,我们可以确定点$Q(a,ab)$在第三象限。
【答案】:C
首先,我们需要明确四个象限的坐标特点:
第一象限:横坐标和纵坐标都为正;
第二象限:横坐标为负,纵坐标为正;
第三象限:横坐标和纵坐标都为负;
第四象限:横坐标为正,纵坐标为负。
根据题意,点$P(-a,b)$在第一象限,那么它的横坐标$-a$为正,即$a$为负;同时,它的纵坐标$b$也为正。
接下来,我们要确定点$Q(a,ab)$的坐标特点。
由于已知$a$为负,$b$为正,那么$ab$为负(因为负数乘以正数得负数)。
所以,点$Q$的横坐标$a$为负,纵坐标$ab$也为负。
根据四个象限的坐标特点,我们可以确定点$Q(a,ab)$在第三象限。
【答案】:C
5. 如图,在观察点O观测到教堂的位置是
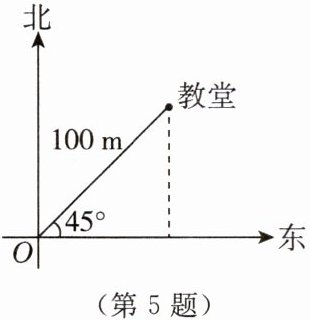
东北方向100m
.
答案:
解:东北方向100m
6. 观察如图所示的象棋棋盘,$(5,1)$表示“帅”的位置,马走“日”字,那么“马8进7”(即第8列的马前进到第7列)后的位置可表示为
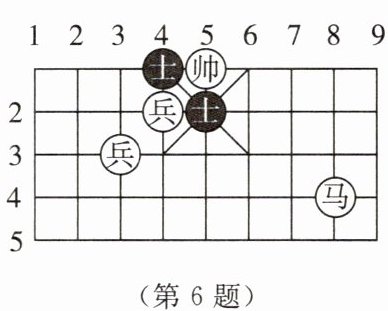
(7,2)
.
答案:
解:由图可知,第8列的马初始位置在第4行,用数对表示为$(8,4)$。马走“日”字,“马8进7”即从第8列前进到第7列,有两种走法:
1. 向右上走“日”字:从$(8,4)$向右平移1列(到第9列,不符合进7列),向左平移1列到第7列,同时向上平移2行,行数变为$4 - 2 = 2$,位置为$(7,2)$;
2. 向右下走“日”字:从$(8,4)$向左平移1列到第7列,同时向下平移2行,行数变为$4 + 2 = 6$,超出棋盘行数(棋盘最大行数为5),此情况不存在。
综上,“马8进7”后的位置为$(7,2)$。
答案:$(7,2)$
1. 向右上走“日”字:从$(8,4)$向右平移1列(到第9列,不符合进7列),向左平移1列到第7列,同时向上平移2行,行数变为$4 - 2 = 2$,位置为$(7,2)$;
2. 向右下走“日”字:从$(8,4)$向左平移1列到第7列,同时向下平移2行,行数变为$4 + 2 = 6$,超出棋盘行数(棋盘最大行数为5),此情况不存在。
综上,“马8进7”后的位置为$(7,2)$。
答案:$(7,2)$
7. [2025·杭州期中]如图,方格纸中的每个小方格都是边长为1个单位的正方形.若学校A的坐标为$(2,1)$,图书馆B的坐标为$(-1,-2)$,解答以下问题:
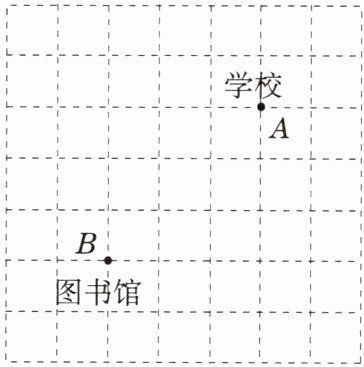
(1)建立相应的平面直角坐标系;
(2)若体育馆C的坐标为$(1,-3)$,请在图中标出体育馆的位置.

(1)建立相应的平面直角坐标系;
(2)若体育馆C的坐标为$(1,-3)$,请在图中标出体育馆的位置.
答案:
【解析】:
(1) 根据题目所给的学校A的坐标$(2,1)$和图书馆B的坐标$(-1,-2)$,可以确定平面直角坐标系。在方格纸上,每个小方格的边长为1个单位,因此可以根据坐标来确定原点的位置。学校A的横坐标为2,纵坐标为1,图书馆B的横坐标为-1,纵坐标为-2。通过这两个点,我们可以确定x轴和y轴的位置,从而建立平面直角坐标系。
(2) 根据体育馆C的坐标$(1,-3)$,我们可以在已经建立的平面直角坐标系中找到对应的点。横坐标为1,纵坐标为-3,因此在图中标出该点即可。
【答案】:
(1) 解:
* 首先,在方格纸上选择一个合适的位置作为原点O。
* 然后,根据学校A的坐标$(2,1)$,确定x轴和y轴的方向和单位长度。具体来说,从原点O出发,向右移动2个单位,向上移动1个单位,到达学校A的位置。
* 同样地,根据图书馆B的坐标$(-1,-2)$,验证x轴和y轴的方向和单位长度是否正确。从原点O出发,向左移动1个单位,向下移动2个单位,应到达图书馆B的位置。
* 最后,画出x轴和y轴,标出原点O和坐标轴上的刻度,完成平面直角坐标系的建立。
(2) 解:
* 在已经建立的平面直角坐标系中,根据体育馆C的坐标$(1,-3)$找到对应的点。
* 从原点O出发,向右移动1个单位,向下移动3个单位,到达体育馆C的位置。
* 在该位置标出体育馆C的符号(如一个圆点或一个小旗子),并注明坐标$(1,-3)$。
(1) 根据题目所给的学校A的坐标$(2,1)$和图书馆B的坐标$(-1,-2)$,可以确定平面直角坐标系。在方格纸上,每个小方格的边长为1个单位,因此可以根据坐标来确定原点的位置。学校A的横坐标为2,纵坐标为1,图书馆B的横坐标为-1,纵坐标为-2。通过这两个点,我们可以确定x轴和y轴的位置,从而建立平面直角坐标系。
(2) 根据体育馆C的坐标$(1,-3)$,我们可以在已经建立的平面直角坐标系中找到对应的点。横坐标为1,纵坐标为-3,因此在图中标出该点即可。
【答案】:
(1) 解:
* 首先,在方格纸上选择一个合适的位置作为原点O。
* 然后,根据学校A的坐标$(2,1)$,确定x轴和y轴的方向和单位长度。具体来说,从原点O出发,向右移动2个单位,向上移动1个单位,到达学校A的位置。
* 同样地,根据图书馆B的坐标$(-1,-2)$,验证x轴和y轴的方向和单位长度是否正确。从原点O出发,向左移动1个单位,向下移动2个单位,应到达图书馆B的位置。
* 最后,画出x轴和y轴,标出原点O和坐标轴上的刻度,完成平面直角坐标系的建立。
(2) 解:
* 在已经建立的平面直角坐标系中,根据体育馆C的坐标$(1,-3)$找到对应的点。
* 从原点O出发,向右移动1个单位,向下移动3个单位,到达体育馆C的位置。
* 在该位置标出体育馆C的符号(如一个圆点或一个小旗子),并注明坐标$(1,-3)$。
8. [2024·厦门第六中学期末]已知点$P(2,-3)$,$Q(2,2)$,下列结论错误的是(
A.点P在第四象限
B.点P到x轴的距离为2
C.$PQ= 5$
D.$PQ// y$轴
B
)A.点P在第四象限
B.点P到x轴的距离为2
C.$PQ= 5$
D.$PQ// y$轴
答案:
【解析】:
本题主要考查了点的坐标性质以及两点间距离的计算,同时涉及了平行于坐标轴的性质。
A选项:点$P(2,-3)$的横坐标为正,纵坐标为负,所以点P在第四象限,这是正确的。
B选项:点$P(2,-3)$到x轴的距离是其纵坐标的绝对值,即$|-3|=3$,不是2,所以这是错误的,但题目要求找出错误的结论,因此B选项符合题意(但我们需要继续检查其他选项以确定它是否是题目要求的错误结论,因为可能有多个错误结论)。
C选项:点$P(2,-3)$和点$Q(2,2)$的横坐标相同,所以PQ垂直于x轴。
两点间的距离公式在这里简化为纵坐标之差的绝对值,即$PQ=|2-(-3)|=5$,所以C选项是正确的。
D选项:由于点P和点Q的横坐标相同,所以线段PQ平行于y轴,这是正确的。
综上所述,B选项中的说法“点P到x轴的距离为2”是错误的,但我们需要确认它是否是题目要求的错误结论(因为题目可能有多选的情况,但本题为单选)。
检查完所有选项后,我们可以确定B选项是题目要求的错误结论,因为其他选项都是正确的。
【答案】:
B
本题主要考查了点的坐标性质以及两点间距离的计算,同时涉及了平行于坐标轴的性质。
A选项:点$P(2,-3)$的横坐标为正,纵坐标为负,所以点P在第四象限,这是正确的。
B选项:点$P(2,-3)$到x轴的距离是其纵坐标的绝对值,即$|-3|=3$,不是2,所以这是错误的,但题目要求找出错误的结论,因此B选项符合题意(但我们需要继续检查其他选项以确定它是否是题目要求的错误结论,因为可能有多个错误结论)。
C选项:点$P(2,-3)$和点$Q(2,2)$的横坐标相同,所以PQ垂直于x轴。
两点间的距离公式在这里简化为纵坐标之差的绝对值,即$PQ=|2-(-3)|=5$,所以C选项是正确的。
D选项:由于点P和点Q的横坐标相同,所以线段PQ平行于y轴,这是正确的。
综上所述,B选项中的说法“点P到x轴的距离为2”是错误的,但我们需要确认它是否是题目要求的错误结论(因为题目可能有多选的情况,但本题为单选)。
检查完所有选项后,我们可以确定B选项是题目要求的错误结论,因为其他选项都是正确的。
【答案】:
B
9. [2024·六安期中]在平面直角坐标系中,点$A(t-3,5-t)$在坐标轴上,下列判断,甲:t可能是3;乙:t可能是5;丙:点A距离原点2个单位.其中正确的是(
A.甲和丙
B.乙和丙
C.甲和乙
D.甲、乙、丙
D
)A.甲和丙
B.乙和丙
C.甲和乙
D.甲、乙、丙
答案:
【解析】:
首先,我们需要明确点A在坐标轴上的条件。点A的坐标为$(t-3,5-t)$。
当点A在x轴上时,其y坐标为0,即$5-t=0$,解得$t=5$。
当点A在y轴上时,其x坐标为0,即$t-3=0$,解得$t=3$。
接下来,我们考虑点A到原点的距离。
使用两点间距离公式,点A到原点的距离为$\sqrt{(t-3)^{2} + (5-t)^{2}}$。
若该距离为2,则我们有方程:
$(t-3)^{2} + (5-t)^{2} = 4$
展开并整理得:
$t^{2} - 6t + 9 + 25 - 10t + t^{2} = 4$
$2t^{2} - 16t + 30 = 0$
$t^{2} - 8t + 15 = 0$
通过因式分解或使用求根公式,我们可以得到$t=3$或$t=5$为该方程的解,但需要验证这两个解是否都满足原方程。
当$t=3$时,代入原方程,得到点A的坐标为$(0,2)$,此时点A到原点的距离为$\sqrt{0^2 + 2^2} = 2$,满足条件。
当$t=5$时,代入原方程,得到点A的坐标为$(2,0)$,此时点A到原点的距离为$\sqrt{2^2 + 0^2} = 2$,也满足条件。
所以甲,乙,丙三个判断都是正确的,但我们需要进一步验证题目中的选项。
【答案】:D。
首先,我们需要明确点A在坐标轴上的条件。点A的坐标为$(t-3,5-t)$。
当点A在x轴上时,其y坐标为0,即$5-t=0$,解得$t=5$。
当点A在y轴上时,其x坐标为0,即$t-3=0$,解得$t=3$。
接下来,我们考虑点A到原点的距离。
使用两点间距离公式,点A到原点的距离为$\sqrt{(t-3)^{2} + (5-t)^{2}}$。
若该距离为2,则我们有方程:
$(t-3)^{2} + (5-t)^{2} = 4$
展开并整理得:
$t^{2} - 6t + 9 + 25 - 10t + t^{2} = 4$
$2t^{2} - 16t + 30 = 0$
$t^{2} - 8t + 15 = 0$
通过因式分解或使用求根公式,我们可以得到$t=3$或$t=5$为该方程的解,但需要验证这两个解是否都满足原方程。
当$t=3$时,代入原方程,得到点A的坐标为$(0,2)$,此时点A到原点的距离为$\sqrt{0^2 + 2^2} = 2$,满足条件。
当$t=5$时,代入原方程,得到点A的坐标为$(2,0)$,此时点A到原点的距离为$\sqrt{2^2 + 0^2} = 2$,也满足条件。
所以甲,乙,丙三个判断都是正确的,但我们需要进一步验证题目中的选项。
【答案】:D。
查看更多完整答案,请扫码查看


