第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
一次函数$y = kx + b$($k$,$b$为常数,且$k \neq 0$)的图象是经过$(0,b)$,$(-\frac{b}{k},0)$两点的一条直线,当$|k|$越大时,一次函数的图象离$y$轴越近,
$b$
是直线$y = kx + b与y$轴的交点的纵坐标,叫作直线$y = kx + b在y$轴上的截距,简称截距。
答案:
【解析】:
题目考查了一次函数图象的基本性质,特别是与坐标轴的交点。对于一次函数$y = kx + b$,当$x=0$时,$y=b$,所以直线与$y$轴的交点坐标为$(0,b)$,这个$b$就是直线在$y$轴上的截距。题目已经给出了这个性质,并要求填写关于截距的定义。
【答案】:
$b$
题目考查了一次函数图象的基本性质,特别是与坐标轴的交点。对于一次函数$y = kx + b$,当$x=0$时,$y=b$,所以直线与$y$轴的交点坐标为$(0,b)$,这个$b$就是直线在$y$轴上的截距。题目已经给出了这个性质,并要求填写关于截距的定义。
【答案】:
$b$
1. [2025·芜湖月考]下面是画一次函数$y = \frac{1}{2}x - 2$的图象的过程(不完整),请补充完整。
(1)列表:
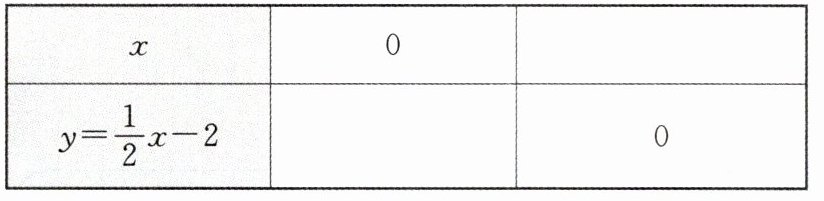
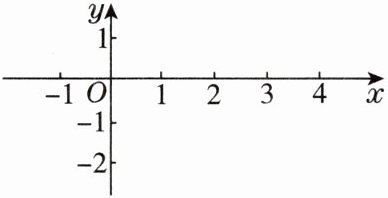
(2)描点、连线,如图。
(1)列表:

(2)描点、连线,如图。

答案:
【解析】:本题考查了一次函数图象的画法,需要我们先根据函数表达式求出与坐标轴的交点,再列表、描点、连线画出函数图象。
对于一次函数$y = \frac{1}{2}x - 2$,我们可以通过给定$x$的值来计算$y$的值,从而完成列表。已知当$x = 0$时,我们需要求出对应的$y$值;同时,已知当$y = 0$时,我们需要求出对应的$x$值。
当$x = 0$时,代入函数$y = \frac{1}{2}x - 2$,得到$y = \frac{1}{2}× 0 - 2 = -2$。
当$y = 0$时,代入函数$y = \frac{1}{2}x - 2$,得到$0 = \frac{1}{2}x - 2$,解这个方程可以得到$x = 4$。
根据以上计算,我们可以列出以下的表格:
| $x$ | $0$ | $4$ |
| $y = \frac{1}{2}x - 2$ | $-2$ | $0$ |
接下来,我们需要在坐标系中描出这两个点$(0, -2)$和$(4, 0)$,并用直线连接它们,从而得到一次函数$y = \frac{1}{2}x - 2$的图象。
【答案】:
(1)列表:
| $x$ | $0$ | $4$ |
| $y = \frac{1}{2}x - 2$ | $-2$ | $0$ |
对于一次函数$y = \frac{1}{2}x - 2$,我们可以通过给定$x$的值来计算$y$的值,从而完成列表。已知当$x = 0$时,我们需要求出对应的$y$值;同时,已知当$y = 0$时,我们需要求出对应的$x$值。
当$x = 0$时,代入函数$y = \frac{1}{2}x - 2$,得到$y = \frac{1}{2}× 0 - 2 = -2$。
当$y = 0$时,代入函数$y = \frac{1}{2}x - 2$,得到$0 = \frac{1}{2}x - 2$,解这个方程可以得到$x = 4$。
根据以上计算,我们可以列出以下的表格:
| $x$ | $0$ | $4$ |
| $y = \frac{1}{2}x - 2$ | $-2$ | $0$ |
接下来,我们需要在坐标系中描出这两个点$(0, -2)$和$(4, 0)$,并用直线连接它们,从而得到一次函数$y = \frac{1}{2}x - 2$的图象。
【答案】:
(1)列表:
| $x$ | $0$ | $4$ |
| $y = \frac{1}{2}x - 2$ | $-2$ | $0$ |
2. 画出一次函数$y = 3x - 3$的图象。
(1)可以先确定这条直线与$x$轴的交点坐标为
(2)请你在图中画出这条直线,并求出这条直线与两条坐标轴围成的三角形的面积。
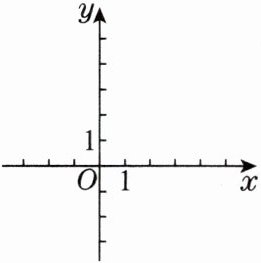
(1)可以先确定这条直线与$x$轴的交点坐标为
(1,0)
,与$y$轴的交点坐标为____(0,-3)
;(2)请你在图中画出这条直线,并求出这条直线与两条坐标轴围成的三角形的面积。

答案:
【解析】:
本题主要考查一次函数图像的画法以及与坐标轴围成的三角形面积的计算。
(1)确定直线与$x$轴和$y$轴的交点坐标。
对于一次函数$y=kx+b$($k$,$b$为常数,$k\neq0$),当$y = 0$时,可求出与$x$轴的交点横坐标;当$x = 0$时,可求出与$y$轴的交点纵坐标。
(2)根据(1)中求出的交点坐标,在坐标系中描出这两个点,然后连接这两个点,即可画出一次函数的图像。
对于直线与两条坐标轴围成的三角形面积,可根据三角形面积公式$S=\frac{1}{2}×底×高$来计算,其中底和高分别为直线与$x$轴、$y$轴交点的横、纵坐标的绝对值。
【答案】:
(1)
解:对于一次函数$y = 3x - 3$,
当$y = 0$时,$0 = 3x - 3$,
移项可得$3x=3$,
解得$x = 1$,
所以与$x$轴的交点坐标为$(1,0)$。
当$x = 0$时,$y = 3×0 - 3=-3$,
所以与$y$轴的交点坐标为$(0,-3)$。
故答案为$(1,0)$;$(0,-3)$。
(2)
图略。
由(1)可知,直线与$x$轴的交点坐标为$(1,0)$,与$y$轴的交点坐标为$(0,-3)$,
那么直线与两条坐标轴围成的三角形的底边长为直线与$x$轴交点的横坐标的绝对值$\vert1\vert = 1$,高为直线与$y$轴交点的纵坐标的绝对值$\vert - 3\vert = 3$。
根据三角形面积公式$S=\frac{1}{2}×底×高$,
可得该三角形面积$S=\frac{1}{2}×1×3=\frac{3}{2}$。
本题主要考查一次函数图像的画法以及与坐标轴围成的三角形面积的计算。
(1)确定直线与$x$轴和$y$轴的交点坐标。
对于一次函数$y=kx+b$($k$,$b$为常数,$k\neq0$),当$y = 0$时,可求出与$x$轴的交点横坐标;当$x = 0$时,可求出与$y$轴的交点纵坐标。
(2)根据(1)中求出的交点坐标,在坐标系中描出这两个点,然后连接这两个点,即可画出一次函数的图像。
对于直线与两条坐标轴围成的三角形面积,可根据三角形面积公式$S=\frac{1}{2}×底×高$来计算,其中底和高分别为直线与$x$轴、$y$轴交点的横、纵坐标的绝对值。
【答案】:
(1)
解:对于一次函数$y = 3x - 3$,
当$y = 0$时,$0 = 3x - 3$,
移项可得$3x=3$,
解得$x = 1$,
所以与$x$轴的交点坐标为$(1,0)$。
当$x = 0$时,$y = 3×0 - 3=-3$,
所以与$y$轴的交点坐标为$(0,-3)$。
故答案为$(1,0)$;$(0,-3)$。
(2)
图略。
由(1)可知,直线与$x$轴的交点坐标为$(1,0)$,与$y$轴的交点坐标为$(0,-3)$,
那么直线与两条坐标轴围成的三角形的底边长为直线与$x$轴交点的横坐标的绝对值$\vert1\vert = 1$,高为直线与$y$轴交点的纵坐标的绝对值$\vert - 3\vert = 3$。
根据三角形面积公式$S=\frac{1}{2}×底×高$,
可得该三角形面积$S=\frac{1}{2}×1×3=\frac{3}{2}$。
3. [知识初练]一次函数$y = -x + 5$的图象是由正比例函数
$y = -x$
的图象向上
平移5
个单位得到的,在$y$轴上的截距是5
。
答案:
【解析】:
本题主要考察一次函数图象的平移性质以及一次函数与坐标轴的交点。
首先,考虑正比例函数的形式,正比例函数一般为$y=kx$,其中$k$为非零常数。
观察给定的一次函数$y = -x + 5$,可以看作是正比例函数$y = -x$向上或向下平移得到的。
由于常数项为5,且为正数,因此是向上平移5个单位。
一次函数在$y$轴上的截距,即当$x=0$时的$y$值。
将$x=0$代入$y = -x + 5$,得到$y=5$,所以在$y$轴上的截距是5。
【答案】:
$y = -x$;上;5;5。
本题主要考察一次函数图象的平移性质以及一次函数与坐标轴的交点。
首先,考虑正比例函数的形式,正比例函数一般为$y=kx$,其中$k$为非零常数。
观察给定的一次函数$y = -x + 5$,可以看作是正比例函数$y = -x$向上或向下平移得到的。
由于常数项为5,且为正数,因此是向上平移5个单位。
一次函数在$y$轴上的截距,即当$x=0$时的$y$值。
将$x=0$代入$y = -x + 5$,得到$y=5$,所以在$y$轴上的截距是5。
【答案】:
$y = -x$;上;5;5。
4. 将直线$y = -2x + 3$向下平移3个单位后所得直线对应的函数表达式为(
A.$y = -2x$
B.$y = 2x + 3$
C.$y = 2x - 3$
D.$y = -2x - 3$
A
)A.$y = -2x$
B.$y = 2x + 3$
C.$y = 2x - 3$
D.$y = -2x - 3$
答案:
【解析】:
本题考查的是一次函数的平移性质。
对于一次函数 $y = kx + b$,若图像向下平移m个单位,则新的函数表达式变为 $y = kx + b - m$。
在本题中,原函数为 $y = -2x + 3$,需要向下平移3个单位。
根据平移性质,新的函数表达式应为 $y = -2x + 3 - 3$。
简化后得到 $y = -2x$。
【答案】:
A. $y = -2x$。
本题考查的是一次函数的平移性质。
对于一次函数 $y = kx + b$,若图像向下平移m个单位,则新的函数表达式变为 $y = kx + b - m$。
在本题中,原函数为 $y = -2x + 3$,需要向下平移3个单位。
根据平移性质,新的函数表达式应为 $y = -2x + 3 - 3$。
简化后得到 $y = -2x$。
【答案】:
A. $y = -2x$。
【变式题】[2024·苏州期中]在平面直角坐标系中,将直线$y = 3x + b$向上平移2个单位后经过点$(0,1)$,则$b$的值为(
A.$-5$
B.$-1$
C.$3$
D.$7$
-1
)A.$-5$
B.$-1$
C.$3$
D.$7$
答案:
【解析】:
本题考查了一次函数图象的平移性质。
根据平移规律,将直线$y = 3x + b$向上平移2个单位后,新的直线方程为$y = 3x + b + 2$。
由于新的直线经过点$(0,1)$,可以将这一点代入新的直线方程中求解$b$。
即,代入点$(0,1)$到方程$y = 3x + b + 2$,得到$1 = 0 + b + 2$。
解这个方程,得到$b = -1$。
【答案】:
B
本题考查了一次函数图象的平移性质。
根据平移规律,将直线$y = 3x + b$向上平移2个单位后,新的直线方程为$y = 3x + b + 2$。
由于新的直线经过点$(0,1)$,可以将这一点代入新的直线方程中求解$b$。
即,代入点$(0,1)$到方程$y = 3x + b + 2$,得到$1 = 0 + b + 2$。
解这个方程,得到$b = -1$。
【答案】:
B
5. 已知直线$y = (2m + 1)x + m - 3平行于直线y = 5x$,则$m$的值为
2
。
答案:
解:因为两直线平行,所以它们的斜率相等。直线$y=(2m + 1)x + m - 3$的斜率为$2m + 1$,直线$y = 5x$的斜率为$5$,则有:
$2m + 1 = 5$
解得$m = 2$
当$m = 2$时,直线$y=(2m + 1)x + m - 3$为$y = 5x - 1$,与直线$y = 5x$不重合,满足平行条件。
故$m$的值为$2$。
$2m + 1 = 5$
解得$m = 2$
当$m = 2$时,直线$y=(2m + 1)x + m - 3$为$y = 5x - 1$,与直线$y = 5x$不重合,满足平行条件。
故$m$的值为$2$。
6. [2025年1月安庆期末]已知一次函数$y = kx + b的图象与直线y = -3x + 4$平行,且截距为$-5$。
(1)求这个函数的表达式;
(2)判断点$A(-\frac{1}{3},-6)$是否在此一次函数的图象上。
(1)求这个函数的表达式;
(2)判断点$A(-\frac{1}{3},-6)$是否在此一次函数的图象上。
答案:
(1)解:因为一次函数$y = kx + b$的图象与直线$y = -3x + 4$平行,所以$k=-3$。又因为截距为$-5$,所以$b=-5$,故这个函数的表达式为$y=-3x-5$。
(2)解:将$x=-\frac{1}{3}$代入$y=-3x-5$,得$y=-3×(-\frac{1}{3})-5=1 - 5=-4$。因为$-4\neq-6$,所以点$A(-\frac{1}{3},-6)$不在此一次函数的图象上。
(1)解:因为一次函数$y = kx + b$的图象与直线$y = -3x + 4$平行,所以$k=-3$。又因为截距为$-5$,所以$b=-5$,故这个函数的表达式为$y=-3x-5$。
(2)解:将$x=-\frac{1}{3}$代入$y=-3x-5$,得$y=-3×(-\frac{1}{3})-5=1 - 5=-4$。因为$-4\neq-6$,所以点$A(-\frac{1}{3},-6)$不在此一次函数的图象上。
查看更多完整答案,请扫码查看


