《2025年点拨训练八年级数学上册沪科版安徽专版》

思维模型 待定系数法

答案： 未知系数

1. [2024·上海中考改编]点$(3,-5)在正比例函数y = kx(k \neq 0)$的图象上,则$k$的值为(D)
A.$-15$
B.$15$
C.$-\frac{3}{5}$
D.$-\frac{5}{3}$

答案： D

2. [2024·厦门期末]已知函数$y = kx + b(k \neq 0)的图象与y$轴交点的纵坐标为1,且当$x = 1$时,$y = 3$,那么此函数的表达式为y=2x+1.

答案： y=2x+1

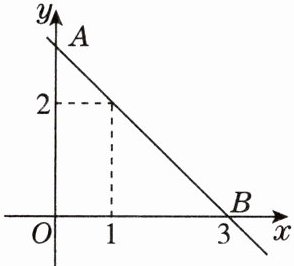
3. 如图,直线$AB$对应的函数表达式为y=-x+3.

答案： y=-x+3

4. [2024·蚌埠期中]写出满足下表关系的一次函数表达式：y=-0.5x+7.

答案： y=-0.5x+7

5. [2025年1月深圳期末]已知$y - 1与x + 2$成正比例,当$x = -3$时,$y = 3$,那么$y与x$之间的函数关系式为y=-2x-3.

答案： y=-2x-3

6. [2025年1月合肥期末]在平面直角坐标系中,一条直线经过$A(-1,5)$,$B(a,-3)$,$C(3,13)$三点.求这条直线所对应的函数表达式以及$a$的值.

答案： 解：这条直线所对应的函数表达式为 y=2x+7,a=-5.

7. [2024·安庆期末]一次函数$y = kx + b的图象经过点(-2,1)$,且平行于直线$y = -2x$,则$b$的值为-3.

答案： -3

8. 已知一次函数$y = (2m + 1)x + m - 2$.
(1)若函数的图象经过原点,求$m$的值；
(2)若函数的图象平行于直线$y = 3x - 5$,求$m$的值.

答案： 解：
(1)因为函数 y=(2m+1)x+m-2 是一次函数，且其图象经过原点，所以 2m+1≠0,0=m-2,解得m=2.
(2)因为函数的图象平行于直线 y=3x-5，所以{2m+1=3，m-2≠-5，所以 m=1.

9. 一支蜡烛长$20\mathrm{cm}$,每分钟燃烧的长度是$2\mathrm{cm}$,蜡烛剩余长度$y(\mathrm{cm})与燃烧时间x(\mathrm{min})$之间的关系式为y=20-2x.(不需要写出自变量的取值范围)

答案： y=20-2x