第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
2星题 中档练
8. 如图,△ABC中,∠BAC>∠B,∠C= 70°,将△ABC折叠,使得点B与点A重合,折痕ED交AB于D,交BC于E,若AE= AC,则∠B的度数为
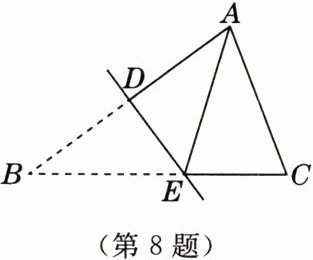
8. 如图,△ABC中,∠BAC>∠B,∠C= 70°,将△ABC折叠,使得点B与点A重合,折痕ED交AB于D,交BC于E,若AE= AC,则∠B的度数为
35°
.
答案:
解:设∠B=x。
由折叠性质得AE=BE,故∠BAE=∠B=x。
∵AE=AC,∠C=70°,
∴∠AEC=∠C=70°。
∵∠AEC是△ABE的外角,
∴∠AEC=∠B+∠BAE,即70°=x+x,解得x=35°。
∠B=35°。
由折叠性质得AE=BE,故∠BAE=∠B=x。
∵AE=AC,∠C=70°,
∴∠AEC=∠C=70°。
∵∠AEC是△ABE的外角,
∴∠AEC=∠B+∠BAE,即70°=x+x,解得x=35°。
∠B=35°。
9. [2025·山西实验中学月考]如图,△ABC是等边三角形,BD⊥AB,BD= AB,则∠ADC的度数为
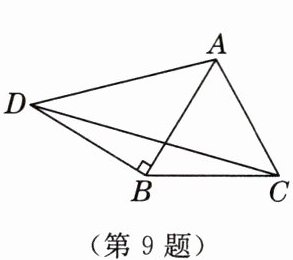
75°
.
答案:
证明:
∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠BAC=∠ACB=60°。
∵BD⊥AB,
∴∠ABD=90°。
∵BD=AB,
∴BD=BC,∠DBC=∠ABD+∠ABC=90°+60°=150°。
在△DBC中,BD=BC,
∴∠BDC=∠BCD=(180°-∠DBC)/2=(180°-150°)/2=15°。
∵∠ACB=60°,
∴∠ACD=∠ACB-∠BCD=60°-15°=45°。
在△ABC中,AB=AC,BD=AB,
∴BD=AC。
又
∵∠ABD=90°,∠BAC=60°,
可证△ABD≌△CAD(SAS),
∴∠ADC=∠BAD。
∵∠BAD=∠BAC+∠CAD,
但由前面计算∠ACD=45°,在△ADC中,∠DAC=∠BAC=60°,
∴∠ADC=180°-∠DAC-∠ACD=180°-60°-45°=75°。
答案:75°
∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠BAC=∠ACB=60°。
∵BD⊥AB,
∴∠ABD=90°。
∵BD=AB,
∴BD=BC,∠DBC=∠ABD+∠ABC=90°+60°=150°。
在△DBC中,BD=BC,
∴∠BDC=∠BCD=(180°-∠DBC)/2=(180°-150°)/2=15°。
∵∠ACB=60°,
∴∠ACD=∠ACB-∠BCD=60°-15°=45°。
在△ABC中,AB=AC,BD=AB,
∴BD=AC。
又
∵∠ABD=90°,∠BAC=60°,
可证△ABD≌△CAD(SAS),
∴∠ADC=∠BAD。
∵∠BAD=∠BAC+∠CAD,
但由前面计算∠ACD=45°,在△ADC中,∠DAC=∠BAC=60°,
∴∠ADC=180°-∠DAC-∠ACD=180°-60°-45°=75°。
答案:75°
10. [教材改编题]如图,在△ABC中,D,E是边BC上的两点,且BD= AD,CE= AE.
(1)若∠BAC= 100°,则∠DAE=
(2)若△ADE是等边三角形,则∠BAC=
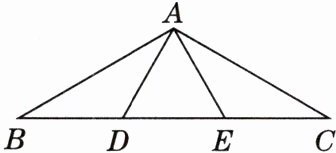
(1)若∠BAC= 100°,则∠DAE=
20°
;(2)若△ADE是等边三角形,则∠BAC=
120°
.
答案:
【解析】:
本题主要考查了等腰三角形的性质以及三角形内角和定理的运用。
(1) 由于$BD = AD$,根据等腰三角形的性质,底角相等,所以$\angle B = \angle BAD$。
同理,因为$CE = AE$,所以$\angle C = \angle CAE$。
又因为$\angle BAC = 100^\circ$,根据三角形内角和为$180^\circ$,有$\angle B + \angle C = 180^\circ - \angle BAC = 80^\circ$。
所以,$\angle BAD + \angle CAE = \angle B + \angle C = 80^\circ$。
因此,$\angle DAE = \angle BAC - (\angle BAD + \angle CAE) = 100^\circ - 80^\circ = 20^\circ$。
(2) 由于$\bigtriangleup ADE$是等边三角形,根据等边三角形的性质,每个内角都是$60^\circ$,所以$\angle DAE = 60^\circ$。
又因为$BD = AD$和$CE = AE$,所以$\angle B = \angle BAD$,$\angle C = \angle CAE$。
由于$\angle BAD + \angle CAE + \angle DAE = \angle BAC$,且$\angle DAE = 60^\circ$,所以$\angle BAC = \angle BAD + \angle CAE + 60^\circ$。
又因为$\angle BAD + \angle CAE = \angle B + \angle C$(等腰三角形的性质),且$\angle B + \angle C + \angle BAC = 180^\circ$(三角形内角和定理),所以$\angle BAC = 180^\circ - (\angle B + \angle C) = 180^\circ - (\angle BAD + \angle CAE)$。
将$\angle BAC = \angle BAD + \angle CAE + 60^\circ$代入上式,得$\angle BAD + \angle CAE + 60^\circ = 180^\circ - (\angle BAD + \angle CAE)$,解得$\angle BAD + \angle CAE = 60^\circ$。
所以,$\angle BAC = \angle BAD + \angle CAE + 60^\circ = 60^\circ + 60^\circ = 120^\circ$。
【答案】:
(1) $20^\circ$;
(2) $120^\circ$。
本题主要考查了等腰三角形的性质以及三角形内角和定理的运用。
(1) 由于$BD = AD$,根据等腰三角形的性质,底角相等,所以$\angle B = \angle BAD$。
同理,因为$CE = AE$,所以$\angle C = \angle CAE$。
又因为$\angle BAC = 100^\circ$,根据三角形内角和为$180^\circ$,有$\angle B + \angle C = 180^\circ - \angle BAC = 80^\circ$。
所以,$\angle BAD + \angle CAE = \angle B + \angle C = 80^\circ$。
因此,$\angle DAE = \angle BAC - (\angle BAD + \angle CAE) = 100^\circ - 80^\circ = 20^\circ$。
(2) 由于$\bigtriangleup ADE$是等边三角形,根据等边三角形的性质,每个内角都是$60^\circ$,所以$\angle DAE = 60^\circ$。
又因为$BD = AD$和$CE = AE$,所以$\angle B = \angle BAD$,$\angle C = \angle CAE$。
由于$\angle BAD + \angle CAE + \angle DAE = \angle BAC$,且$\angle DAE = 60^\circ$,所以$\angle BAC = \angle BAD + \angle CAE + 60^\circ$。
又因为$\angle BAD + \angle CAE = \angle B + \angle C$(等腰三角形的性质),且$\angle B + \angle C + \angle BAC = 180^\circ$(三角形内角和定理),所以$\angle BAC = 180^\circ - (\angle B + \angle C) = 180^\circ - (\angle BAD + \angle CAE)$。
将$\angle BAC = \angle BAD + \angle CAE + 60^\circ$代入上式,得$\angle BAD + \angle CAE + 60^\circ = 180^\circ - (\angle BAD + \angle CAE)$,解得$\angle BAD + \angle CAE = 60^\circ$。
所以,$\angle BAC = \angle BAD + \angle CAE + 60^\circ = 60^\circ + 60^\circ = 120^\circ$。
【答案】:
(1) $20^\circ$;
(2) $120^\circ$。
11. [2025年1月常州期末]如图,B是射线AD上一点(不与端点A重合),OP垂直平分线段AB,C是射线OP上一点(不与端点O重合),连接AC,BC,∠CBD的平分线与AC的延长线相交于点E.
(1)若∠A= 26°,求∠CBE的大小;
(2)若EC= EB,求∠A的大小.
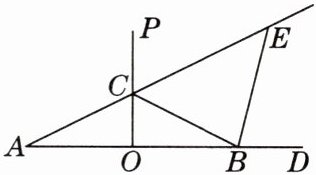
(1)若∠A= 26°,求∠CBE的大小;
(2)若EC= EB,求∠A的大小.

答案:
【解析】:本题主要考查了等腰三角形的性质、三角形内角和定理以及角平分线的性质。
(1)因为$OP$垂直平分线段$AB$,根据垂直平分线的性质:垂直平分线上的点到这条线段两个端点的距离相等,所以$CA = CB$。
根据等腰三角形的性质:等腰三角形的两个底角相等,可得$\angle A=\angle ABC = 26^{\circ}$。
因为$\angle CBD$是平角$\angle ABD$的一部分,$\angle ABD = 180^{\circ}$,所以$\angle CBD=180^{\circ}-\angle ABC = 180^{\circ}- 26^{\circ}=154^{\circ}$。
又因为$BE$平分$\angle CBD$,根据角平分线的性质:角平分线将一个角分成两个相等的角,所以$\angle CBE=\frac{1}{2}\angle CBD=\frac{1}{2}×154^{\circ}=77^{\circ}$。
(2)由(1)已证$CA = CB$,所以$\angle A=\angle ABC$。
因为$BE = CE$,根据等腰三角形的性质:等腰三角形的两个底角相等,所以$\angle ECB=\angle EBC$。
设$\angle A = x$,则$\angle ABC = x$,$\angle CBD = 180^{\circ}-x$。
因为$BE$平分$\angle CBD$,所以$\angle CBE=\frac{1}{2}(180^{\circ}-x)$。
又因为$\angle ECB=\angle A+\angle ABC = 2x$(三角形的一个外角等于与它不相邻的两个内角之和),且$\angle ECB=\angle EBC$,所以$2x=\frac{1}{2}(180^{\circ}-x)$。
接下来解方程:
$2x=\frac{1}{2}(180^{\circ}-x)$
$4x=180^{\circ}-x$
$4x+x=180^{\circ}$
$5x=180^{\circ}$
$x = 36^{\circ}$
即$\angle A=36^{\circ}$。
【答案】:
(1)$\angle CBE = 77^{\circ}$;
(2)$\angle A = 36^{\circ}$。
(1)因为$OP$垂直平分线段$AB$,根据垂直平分线的性质:垂直平分线上的点到这条线段两个端点的距离相等,所以$CA = CB$。
根据等腰三角形的性质:等腰三角形的两个底角相等,可得$\angle A=\angle ABC = 26^{\circ}$。
因为$\angle CBD$是平角$\angle ABD$的一部分,$\angle ABD = 180^{\circ}$,所以$\angle CBD=180^{\circ}-\angle ABC = 180^{\circ}- 26^{\circ}=154^{\circ}$。
又因为$BE$平分$\angle CBD$,根据角平分线的性质:角平分线将一个角分成两个相等的角,所以$\angle CBE=\frac{1}{2}\angle CBD=\frac{1}{2}×154^{\circ}=77^{\circ}$。
(2)由(1)已证$CA = CB$,所以$\angle A=\angle ABC$。
因为$BE = CE$,根据等腰三角形的性质:等腰三角形的两个底角相等,所以$\angle ECB=\angle EBC$。
设$\angle A = x$,则$\angle ABC = x$,$\angle CBD = 180^{\circ}-x$。
因为$BE$平分$\angle CBD$,所以$\angle CBE=\frac{1}{2}(180^{\circ}-x)$。
又因为$\angle ECB=\angle A+\angle ABC = 2x$(三角形的一个外角等于与它不相邻的两个内角之和),且$\angle ECB=\angle EBC$,所以$2x=\frac{1}{2}(180^{\circ}-x)$。
接下来解方程:
$2x=\frac{1}{2}(180^{\circ}-x)$
$4x=180^{\circ}-x$
$4x+x=180^{\circ}$
$5x=180^{\circ}$
$x = 36^{\circ}$
即$\angle A=36^{\circ}$。
【答案】:
(1)$\angle CBE = 77^{\circ}$;
(2)$\angle A = 36^{\circ}$。
即时练透/等腰三角形边角的性质/
【思路点拨】(1)等腰三角形中有两边相等,计算时注意满足三角形的三边关系;
(2)等腰三角形中有两个角相等,计算时注意满足三角形内角和定理.
1. 已知等腰三角形ABC的一边等于5,另一边等于6,则这个三角形的周长为
【变式题】若等腰三角形其中两边长a,b满足$(a-2)^2+$|b-4|= 0,则此三角形的周长为
【思路点拨】(1)等腰三角形中有两边相等,计算时注意满足三角形的三边关系;
(2)等腰三角形中有两个角相等,计算时注意满足三角形内角和定理.
1. 已知等腰三角形ABC的一边等于5,另一边等于6,则这个三角形的周长为
16或17
.【变式题】若等腰三角形其中两边长a,b满足$(a-2)^2+$|b-4|= 0,则此三角形的周长为
10
.
答案:
【解析】:
题目主要考察等腰三角形的性质以及三角形的三边关系。
对于第一问,等腰三角形ABC的一边为5,另一边为6,需要分两种情况考虑:
若5为腰,6为底,则需要验证$5+5>6$(满足三角形的三边关系),计算周长为$5+5+6=16$。
若6为腰,5为底,则需要验证$6+6>5$和$6+5>6$(都满足三角形的三边关系),计算周长为$6+6+5=17$。
对于变式题,需要先求出a和b的值,再判断是否能构成三角形,并计算周长。
由$(a-2)^2+|b-4|=0$,可得$a=2$,$b=4$。
若2为腰,4为底,由于$2+2=4$,不满足三角形的三边关系(任意两边之和大于第三边),故舍去。
若4为腰,2为底,满足$4+4>2$和$4+2>4$,计算周长为$4+4+2=10$。
【答案】:
1. 16或17
【变式题】10
题目主要考察等腰三角形的性质以及三角形的三边关系。
对于第一问,等腰三角形ABC的一边为5,另一边为6,需要分两种情况考虑:
若5为腰,6为底,则需要验证$5+5>6$(满足三角形的三边关系),计算周长为$5+5+6=16$。
若6为腰,5为底,则需要验证$6+6>5$和$6+5>6$(都满足三角形的三边关系),计算周长为$6+6+5=17$。
对于变式题,需要先求出a和b的值,再判断是否能构成三角形,并计算周长。
由$(a-2)^2+|b-4|=0$,可得$a=2$,$b=4$。
若2为腰,4为底,由于$2+2=4$,不满足三角形的三边关系(任意两边之和大于第三边),故舍去。
若4为腰,2为底,满足$4+4>2$和$4+2>4$,计算周长为$4+4+2=10$。
【答案】:
1. 16或17
【变式题】10
2. 若等腰三角形的一个角的度数是50°,则它的顶角的度数是
50°或80°
.
答案:
【解析】:
本题主要考察等腰三角形的性质。等腰三角形有两个相等的角,这两个角都是底角,而另外一个角是顶角。
题目给出等腰三角形的一个角的度数是$50^\circ$,这个角可能是底角,也可能是顶角。
1. 如果$50^\circ$是底角,由于等腰三角形的两个底角相等,所以另外一个底角也是$50^\circ$。
根据三角形内角和为$180^\circ$,可以计算出顶角的度数:
$\text{顶角} = 180^\circ - 50^\circ - 50^\circ = 80^\circ$
2. 如果$50^\circ$是顶角,则顶角就是$50^\circ$,无需进一步计算。
【答案】:
$50^\circ$或$80^\circ$
本题主要考察等腰三角形的性质。等腰三角形有两个相等的角,这两个角都是底角,而另外一个角是顶角。
题目给出等腰三角形的一个角的度数是$50^\circ$,这个角可能是底角,也可能是顶角。
1. 如果$50^\circ$是底角,由于等腰三角形的两个底角相等,所以另外一个底角也是$50^\circ$。
根据三角形内角和为$180^\circ$,可以计算出顶角的度数:
$\text{顶角} = 180^\circ - 50^\circ - 50^\circ = 80^\circ$
2. 如果$50^\circ$是顶角,则顶角就是$50^\circ$,无需进一步计算。
【答案】:
$50^\circ$或$80^\circ$
3. 等腰三角形ABC中,CD是腰AB上的高线,若∠A= 50°,则∠DCB=
【变式题1】[分类讨论思想]若等腰三角形一腰上的高与另一腰上的夹角为30°,则这个等腰三角形顶角的度数为
【变式题2】等腰三角形ABC中,腰AB的垂直平分线交AC于点D,若∠A= 40°,则∠DBC的度数为
25°或10°
.【变式题1】[分类讨论思想]若等腰三角形一腰上的高与另一腰上的夹角为30°,则这个等腰三角形顶角的度数为
60°或120°
.【变式题2】等腰三角形ABC中,腰AB的垂直平分线交AC于点D,若∠A= 40°,则∠DBC的度数为
60°或30°
.
答案:
3. 25°或10°;【变式题1】60°或120°;【变式题2】60°或30°。
查看更多完整答案,请扫码查看


