《2025年点拨训练八年级数学上册沪科版安徽专版》

10. 已知一次函数的图象经过点$A(0,3)$,且与两坐标轴所围成的三角形的面积为3,则这个一次函数的表达式为(C)
A.$y = 1.5x + 3$
B.$y = -1.5x + 3$
C.$y = 1.5x + 3或y = -1.5x + 3$
D.无法确定

答案： C

11. [2025·淮北月考]已知一直线$y = kx + b平行于直线y = -5x$,且经过直线$y = 4x - 3上的点(1,m)$,则该直线对应的函数表达式为y=-5x+6.

答案： y=-5x+6

12. [2024·马鞍山月考]对于一次函数$y = kx + b$,当$2 \leq x \leq 4$时,$3 \leq y \leq 6$,则该一次函数的表达式为y=3/2x 或 y=-3/2x+9.

答案： y=3/2x 或 y=-3/2x+9

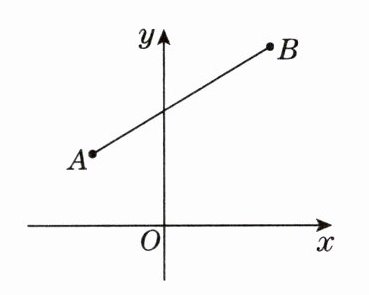
13. 如图,在平面直角坐标系中,$A(-2,2)$,$B(3,5)$,直线$y = kx - k + 1(k \neq 0)与线段AB$有公共点.
(1)直线$y = kx - k + 1$一定经过点(1,1)；
(2)$k$的取值范围是k≤-1/3 或 k≥2.

答案：
(1)(1,1)
(2)k≤-1/3 或 k≥2

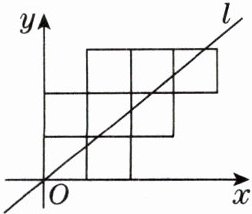
14. [2024·阜阳月考]八个边长为1的正方形如图摆放,经过原点的一条直线$l$将这八个正方形分成面积相等的两部分,则直线$l$对应的函数表达式是y=9/10x.

答案： y=9/10x

15. [2025·咸阳模拟改编]在2025年春晚的舞台上,名为《秧BOT》的创新节目惊艳亮相！这场科技与艺术的跨界盛宴不仅是一场精彩的表演,更是中国机器人产业“软硬协同”能力的集中展现.机器人爱好者李祎同学为了解某种搬运机器人的工作效率,将一台机器人的搬运时间$x(\mathrm{h})和目的地货物总量y(\mathrm{kg})$记录如下表：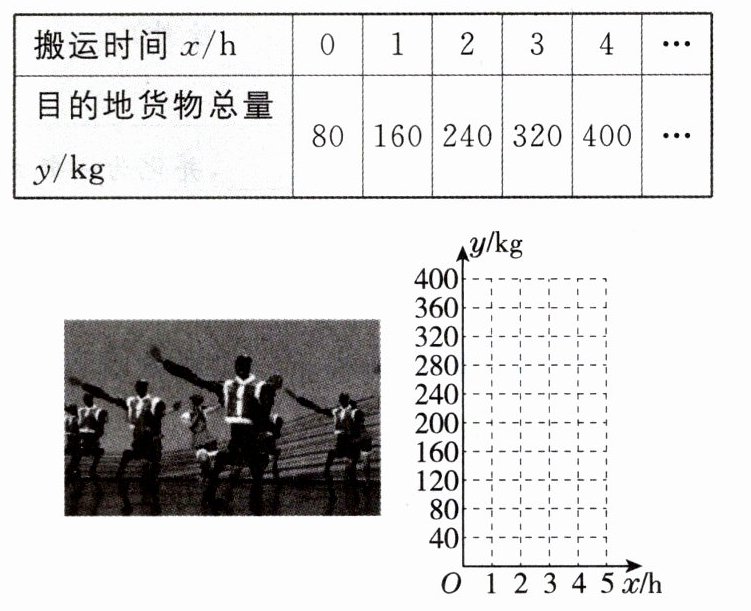
(1)在平面直角坐标系中描出表中数据对应的点,目的地货物总量与这台机器人的搬运时间符合的是一次函数关系；(填“一次”或“正比例”)
(2)根据以上判断,求$y关于x$的函数关系式；
(3)当目的地货物总量为$560\mathrm{kg}$时,这台机器人的搬运时间是多少？

答案： 解：
(1)画图略.一次
(2)设 y 与 x 之间的函数关系式为 y=kx+b(k≠0)，根据题意，得{k+b=160，2k+b=240，解得{k=80，b=80，所以 y 关于 x 的函数关系式为 y=80x+80.
(3)当 y=560 时，80x+80=560，解得 x=6，所以当目的地货物总量为 560 kg 时，这台机器人的搬运时间是 6 h.