第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图,在直角三角形 ABC 中,$∠ACB = 90^{\circ}$,CD 是边 AB 上的高,$AB = 10cm$,$BC = 8cm$,$AC = 6cm$,则$\triangle ABC$的面积为
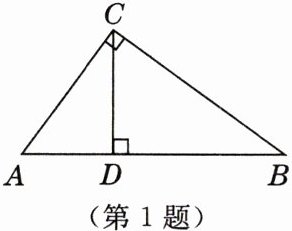
24 cm²
,CD 的长为4.8 cm
.
答案:
24 cm²;4.8 cm
【变式题】如图,在$\triangle ABC$中,CD 和 BE 分别是边 AB,AC 上的高,若$CD = 12$,$BE = 16$,则$\frac{AC}{AB}$的值为(
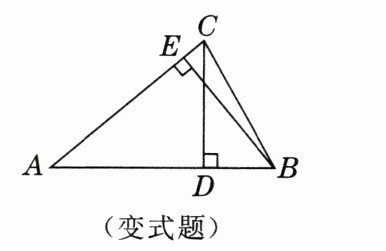
A.$\frac{3}{5}$
B.$\frac{3}{4}$
C.$\frac{4}{3}$
D.$\frac{5}{8}$
B
)
A.$\frac{3}{5}$
B.$\frac{3}{4}$
C.$\frac{4}{3}$
D.$\frac{5}{8}$
答案:
B
2. 创新题·新设问 数学活动课上,老师让同学们自己谈谈对三角形相关知识的理解. 小峰说:“存在这样的三角形,它的三条高之比可以为$1:1:2$,$1:2:3$,$2:3:4$,$3:4:5$.”老师说有一个三角形是不存在的. 你认为不存在的三角形的三条高之比是(
A.$1:1:2$
B.$1:2:3$
C.$2:3:4$
D.$3:4:5$
B
)A.$1:1:2$
B.$1:2:3$
C.$2:3:4$
D.$3:4:5$
答案:
B
3. 创新题·新考法 [2025·滁州月考]三角形中长为 a,b,c 的边上的高分别为$h_{a}$,$h_{b}$,$h_{c}$. 若$a\leqslant h_{a}$,$b\leqslant h_{b}$,则此三角形为(
A.等腰非直角三角形
B.等腰直角三角形
C.直角非等腰三角形
D.以上结论都不对
B
)A.等腰非直角三角形
B.等腰直角三角形
C.直角非等腰三角形
D.以上结论都不对
答案:
B
4. [2025 年 1 月运城期末]如图,小明在计算机上用绘图软件画了一个$Rt\triangle ABC$,$∠C = 90^{\circ}$,并画了两个锐角的平分线 AD 和 BE 及其交点 F,小明发现,无论$Rt\triangle ABC$的形状和大小怎样变化,$∠AFB$的度数都是定值,则这个定值为(
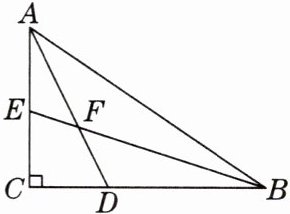
A.$135^{\circ}$
B.$150^{\circ}$
C.$120^{\circ}$
D.$110^{\circ}$
A
)
A.$135^{\circ}$
B.$150^{\circ}$
C.$120^{\circ}$
D.$110^{\circ}$
答案:
A
5. 如图,AD 是$\triangle ABC$的角平分线,$DE// AB$.
(1) 若$DF// AC$,EF 交 AD 于点 O. 试问:DO 是不是$\triangle DEF$的角平分线?并说明理由.
(2) 若 DO 是$\triangle DEF$的角平分线,试探索 DF 与 AC 的位置关系,并说明理由.
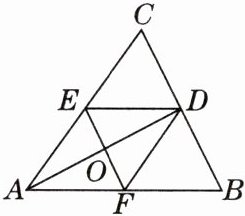
(1) 若$DF// AC$,EF 交 AD 于点 O. 试问:DO 是不是$\triangle DEF$的角平分线?并说明理由.
(2) 若 DO 是$\triangle DEF$的角平分线,试探索 DF 与 AC 的位置关系,并说明理由.

答案:
解:
(1)DO是△DEF的角平分线.理由略.
(2)DF//AC.理由略.
(1)DO是△DEF的角平分线.理由略.
(2)DF//AC.理由略.
6. [2025 年 1 月合肥期末]如图,已知 AD 为$\triangle ABC$的中线,$AB = 10cm$,$AC = 7cm$,$\triangle ACD$的周长为 18 cm,则$\triangle ABD$的周长为
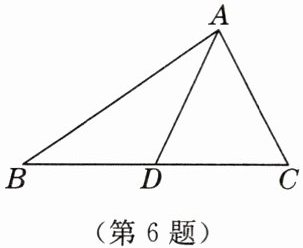
21
cm.
答案:
21
7. 如图,在$\triangle ABC$中,D 是 BC 边上的一点,E,F 分别是 AD,BE 的中点,连接 CE,CF,若$S_{\triangle CEF} = 5$,则$\triangle ABC$的面积为(
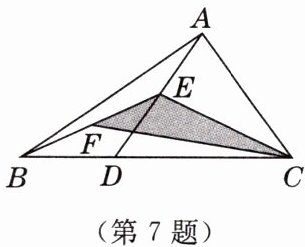
A.15
B.20
C.25
D.30
B
)
A.15
B.20
C.25
D.30
答案:
B
查看更多完整答案,请扫码查看


