《2025年点拨训练八年级数学上册沪科版安徽专版》

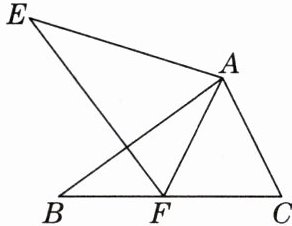
9. 如图,△ABC≌△AEF,有下列结论：
①AC= AF；②EF= BC；③∠EAB= ∠FAC；④∠EAB= ∠EFB.其中正确结论的个数是(C)

A.1
B.2
C.3
D.4

答案： C

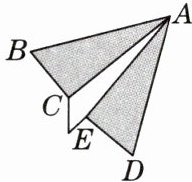
10. 如图所示的是纸飞机的示意图,在折纸的过程中,使得△ABC与△ADE能够重合.如果∠BAC= 25°,∠B= 65°,那么∠DEA的度数为90°.

答案： 90

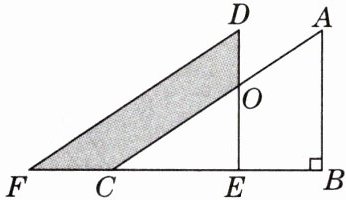
11. 在△ABC中,∠B= 90°,AB= 5,将△ABC沿BC方向平移3个单位至△DEF处,如图所示,边DE与AC交于点O.如果OD= 2,那么图中阴影部分的面积是12.

答案： 12

12. 分类讨论思想 已知△ABC的三边长分别是4,x,9,△DEF的三边长分别为4,2x-7,y,若这两个三角形全等,则2x-y的值等于5 或 8.

答案： 5 或 8

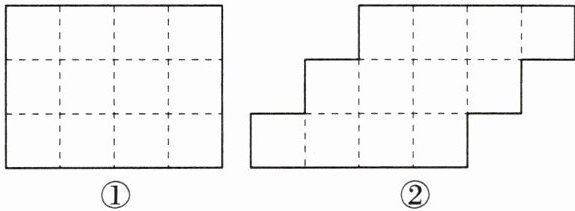
13. 高阶思维·创新能力 如图,沿图形中的虚线,分别把下面的图形划分为两个全等图形.

答案： 【解析】：本题要求沿图形中的虚线将图形划分为两个全等图形，需要利用全等图形的性质，即两个图形能够完全重合。我们需要观察图形的特点，找到合适的切割方式。图①是一个规则的网格图形，可以通过中间的一条竖线或横线将其划分为两个全等图形。图②是一个不规则的图形，需要找到一条合适的虚线，使得切割后的两部分能够完全重合。
【答案】：图①：在第二列的中间处竖着切一刀，将图形划分为两个全等图形（答案不唯一）；
图②：在第二列的中间处竖着切一刀，将图形划分为两个全等图形（答案不唯一）。
图略。

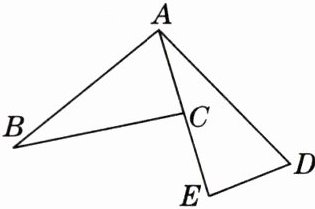
14. [2025·深圳期中]如图,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1) 求证：BC= DE+CE；
(2) 当△ABC满足什么条件时,BC//DE？

答案：
(1)证明:
∵△ABC≌△DAE,
∴BC=AE,AC=DE.又
∵AE=AC+CE,
∴BC=DE+CE.
(2)解：当△ABC 满足∠ACB 为直角时,BC//DE.

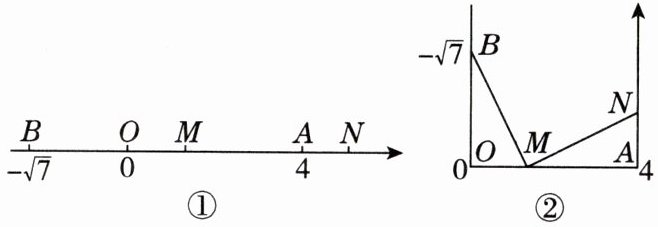
15. 创新题·新考法 如图①,数轴上从左至右依次有B,O,M,A,N五个点,其中点B,O,A表示的数分别为-√7,0,4.如图②,将数轴在点O左侧的部分绕点O顺时针方向旋转90°,将数轴在点A右侧的部分绕点A逆时针方向旋转90°,连接BM,MN.若△OBM和△AMN全等,则点M表示的数为$4-\sqrt{7}$或 2.

答案： $4-\sqrt{7}$或 2