第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
两角及其
1星题 基础题
知识点1 判定三角形全等的基本事实:“角边角”
夹边
分别相等的两个三角形全等. 简记为“角边角”或“ASA”.1星题 基础题
知识点1 判定三角形全等的基本事实:“角边角”
答案:
夹边
1. 如图,已知$△ABC$的三条边和三个角,则甲、乙两个三角形中,与$△ABC$全等的是(
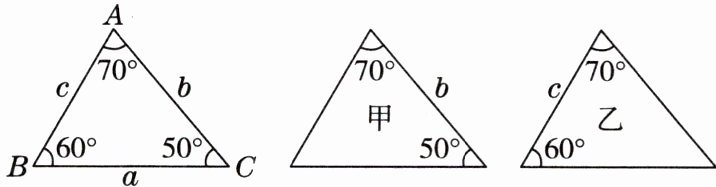
A.甲
B.乙
C.甲和乙
D.都不是
C
)
A.甲
B.乙
C.甲和乙
D.都不是
答案:
C
2. [2025·宿迁期中]如图,已知$∠ACB= ∠ACD$,要直接用“ASA”说明$△ABC\cong △ADC$,则需添加的一个条件是
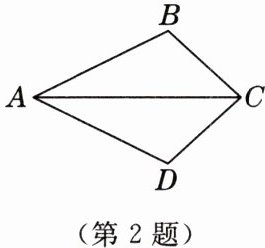
∠BAC=∠DAC
.
答案:
∠BAC=∠DAC
3. [2024·南通中考改编]如图,已知$AB// CF$,E为DF的中点,若$AB= 13cm,CF= 6cm$,则BD的长为
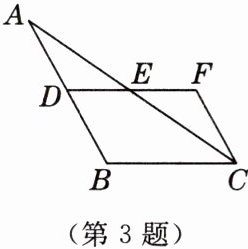
7
cm.
答案:
7
4. 如图,B,C,F,E在同一条直线上,$AC// FD,AB// DE,BC= EF$. 求证:$△ABC\cong △DEF$.
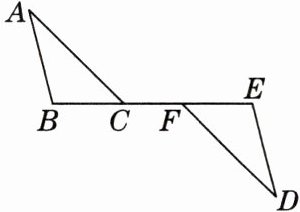
证明:
∵$AC// FD$,
∴$\angle ACB = \angle DFE$(两直线平行,内错角相等)。
∵$AB// DE$,
∴$\angle ABC = \angle DEF$(两直线平行,同位角相等)。
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle ABC = \angle DEF \\BC = EF \\\angle ACB = \angle DFE\end{cases}$
∴$\triangle ABC\cong \triangle DEF(ASA)$。

证明:
∵$AC// FD$,
∴$\angle ACB = \angle DFE$(两直线平行,内错角相等)。
∵$AB// DE$,
∴$\angle ABC = \angle DEF$(两直线平行,同位角相等)。
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle ABC = \angle DEF \\BC = EF \\\angle ACB = \angle DFE\end{cases}$
∴$\triangle ABC\cong \triangle DEF(ASA)$。
答案:
【解析】:本题考查全等三角形的证明,根据题目所给条件$AC// FD,AB// DE,BC= EF$,可以利用平行线的性质,得到对应角相等,再结合已知的边相等,利用$ASA$(角边角)判定定理来证明两个三角形全等
【答案】:证明:
∵$AC// FD$,
∴$\angle ACB = \angle DFE$(两直线平行,内错角相等)。
∵$AB// DE$,
∴$\angle ABC = \angle DEF$(两直线平行,同位角相等)。
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle ABC = \angle DEF \\BC = EF \\\angle ACB = \angle DFE\end{cases}$
∴$\triangle ABC\cong \triangle DEF(ASA)$。
【答案】:证明:
∵$AC// FD$,
∴$\angle ACB = \angle DFE$(两直线平行,内错角相等)。
∵$AB// DE$,
∴$\angle ABC = \angle DEF$(两直线平行,同位角相等)。
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle ABC = \angle DEF \\BC = EF \\\angle ACB = \angle DFE\end{cases}$
∴$\triangle ABC\cong \triangle DEF(ASA)$。
5. [2024·淮南期中]如图,在$△ABC$中,D是BC上一点,$AC= AE$,E是$△ABC$外一点,$∠C= ∠E,∠BAD= ∠CAE$. 求证:$BC= DE$.
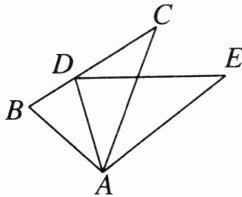

答案:
证明:
∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE.在△BAC和△DAE中,$\left\{\begin{array}{l} ∠BAC=∠DAE,\\ AC=AE,\\ ∠C=∠E,\end{array}\right. $$\therefore \triangle BAC\cong \triangle DAE(ASA)$,$\therefore BC=DE$.
∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE.在△BAC和△DAE中,$\left\{\begin{array}{l} ∠BAC=∠DAE,\\ AC=AE,\\ ∠C=∠E,\end{array}\right. $$\therefore \triangle BAC\cong \triangle DAE(ASA)$,$\therefore BC=DE$.
6. 真实情境 一块三角形玻璃被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是
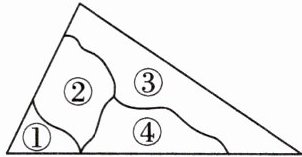
③
.
答案:
③
7. 创新题·新设问 计划测量一片湖的宽度AB,现采用如图所示的方案:
①过点A作$CA⊥AB$于点A,且点C在AB的下方;
②连接BC,从点C处进行观测,在BA的延长线上找一点$B'$,使$∠B'CA= ∠BCA$. 现只需测量一条线段的长,这条线段是
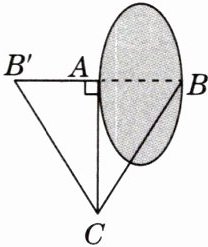
①过点A作$CA⊥AB$于点A,且点C在AB的下方;
②连接BC,从点C处进行观测,在BA的延长线上找一点$B'$,使$∠B'CA= ∠BCA$. 现只需测量一条线段的长,这条线段是
$AB'$
.
答案:
$AB'$
查看更多完整答案,请扫码查看


