第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. [2024·淄博月考]如图,已知$△ABC的面积为10cm^{2}$,AD平分$∠BAC且AD⊥BD$于点D,则$△ADC$的面积为
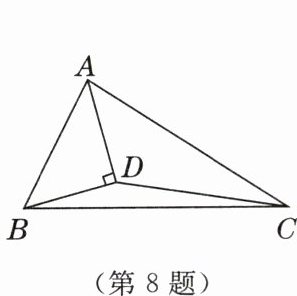
$5\ cm^2$
.
答案:
$5\ \text{cm}^2$
9. 分类讨论思想 [2025·临汾期中]如图,$AB// CE,AB= 10cm$,点D是BC的中点,点P从点A出发,沿$A→B→A$的方向以2 cm/s的速度运动,点Q从点C出发,沿射线CE以1 cm/s的速度运动,当点P到达点A时,P,Q两点同时停止运动,当线段PQ经过点D时,点Q的运动时间为
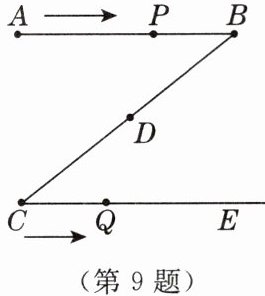
$\frac {10}{3}\ s$或10 s
.
答案:
$\frac {10}{3}\ \text{s}$或10 s
10. [2025年1月合肥期末改编]如图,在$△ABC$中,$AB= AC$,点D,E分别是边AC,BC上一点,连接AE,BD交于点G. 点F是AE上一点,连接CF,若$∠BAC= ∠BGE= ∠EFC$,求证:$AG= CF$.
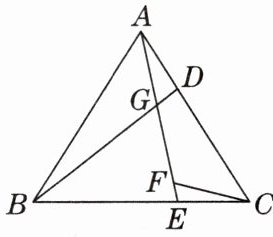

答案:
证明:
∵∠BAC=∠BGE,∠AGB=∠BGE(对顶角相等),
∴∠BAC=∠AGB。
∵∠ABG+∠AGB+∠BAG=180°,∠ACE+∠BAC+∠AEC=180°,
又∠BAC=∠AGB,∠BAG=∠BAC-∠GAC,∠AEC=∠BGE+∠GBE(三角形外角性质),
且∠BGE=∠BAC,
∴∠AEC=∠BAC+∠GBE。
∵AB=AC,
∴∠ABC=∠ACB(等边对等角),即∠ABG+∠GBE=∠ACE。
设∠BAC=∠AGB=∠BGE=∠EFC=α,∠ABG=β,则∠ACE=β+∠GBE,∠AEC=α+∠GBE。
在△AGB中,β+α+∠BAG=180°,
∴∠BAG=180°-α-β。
在△AEC中,∠ACE+α+∠AEC=180°,即(β+∠GBE)+α+(α+∠GBE)=180°,化简得β+2∠GBE+2α=180°,
∴∠GBE=(180°-β-2α)/2。
∵∠EFC=α,∠EFC+∠FEC+∠FCE=180°,∠FEC=∠AEC=α+∠GBE,
∴α+(α+∠GBE)+∠FCE=180°,
∴∠FCE=180°-2α-∠GBE=180°-2α-(180°-β-2α)/2=(2β)/2=β,即∠FCE=β=∠ABG。
∵∠AGB=∠EFC=α,AB=AC,
∴△ABG≌△FCE(AAS),
∴AG=CF。
∵∠BAC=∠BGE,∠AGB=∠BGE(对顶角相等),
∴∠BAC=∠AGB。
∵∠ABG+∠AGB+∠BAG=180°,∠ACE+∠BAC+∠AEC=180°,
又∠BAC=∠AGB,∠BAG=∠BAC-∠GAC,∠AEC=∠BGE+∠GBE(三角形外角性质),
且∠BGE=∠BAC,
∴∠AEC=∠BAC+∠GBE。
∵AB=AC,
∴∠ABC=∠ACB(等边对等角),即∠ABG+∠GBE=∠ACE。
设∠BAC=∠AGB=∠BGE=∠EFC=α,∠ABG=β,则∠ACE=β+∠GBE,∠AEC=α+∠GBE。
在△AGB中,β+α+∠BAG=180°,
∴∠BAG=180°-α-β。
在△AEC中,∠ACE+α+∠AEC=180°,即(β+∠GBE)+α+(α+∠GBE)=180°,化简得β+2∠GBE+2α=180°,
∴∠GBE=(180°-β-2α)/2。
∵∠EFC=α,∠EFC+∠FEC+∠FCE=180°,∠FEC=∠AEC=α+∠GBE,
∴α+(α+∠GBE)+∠FCE=180°,
∴∠FCE=180°-2α-∠GBE=180°-2α-(180°-β-2α)/2=(2β)/2=β,即∠FCE=β=∠ABG。
∵∠AGB=∠EFC=α,AB=AC,
∴△ABG≌△FCE(AAS),
∴AG=CF。
11. 创新题·探究题 如图,在$△ABC$中,$AB= AC,∠BAC= 90^{\circ }$,D是AB上的一动点(不与点A,B重合),$BE⊥CD$交CD的延长线于点E,交CA的延长线于点F.
(1)当点D在AB上时,求证:
①$DA= FA$;②$AB= FA+BD$.
(2)当点D在AB的延长线上时,请你探索AB,FA,BD这三条线段之间的数量关系,画出图形并证明你的结论.
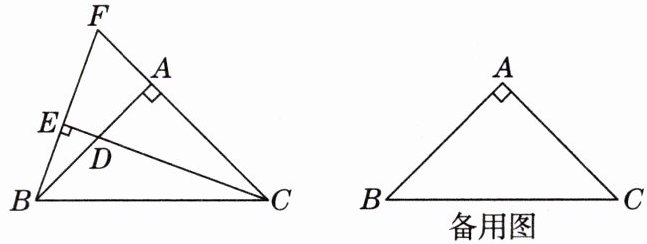
(1)当点D在AB上时,求证:
①$DA= FA$;②$AB= FA+BD$.
(2)当点D在AB的延长线上时,请你探索AB,FA,BD这三条线段之间的数量关系,画出图形并证明你的结论.

答案:
(1)证明:①
∵BE⊥直线CD,
∴∠FEC=90°,
∴∠F+∠DCA=90°.
∵∠BAC=90°,
∴∠FAB=90°=∠DAC.
∴∠F+∠FBA=90°,
∴∠FBA=∠DCA.在△FAB和△DAC中,$\left\{\begin{array}{l} ∠FAB=∠DAC,\\ AB=AC,\\ ∠FBA=∠DCA,\end{array}\right. $$\therefore \triangle FAB\cong \triangle DAC(ASA)$,$\therefore DA=FA$.②由①知$FA=DA$,$\therefore AB=AD+BD=FA+BD$.
(2)解:$AB=FA-BD$.所画图形如图所示.证明:
∵BE⊥直线CD,$\therefore ∠FED=90^{\circ }$,$\therefore ∠F+∠DCA=90^{\circ }$.$\because ∠BAC=90^{\circ }$,$\therefore ∠FAB=90^{\circ }=∠DAC$.$\therefore ∠F+∠FBA=90^{\circ }$,$\therefore ∠FBA=∠DCA$.在△FAB和△DAC中,$\left\{\begin{array}{l} ∠FAB=∠DAC,\\ AB=AC,\\ ∠FBA=∠DCA,\end{array}\right. $$\therefore \triangle FAB\cong \triangle DAC(ASA)$,$\therefore FA=DA$,$\therefore AB=AD-BD=FA-BD$.
(1)证明:①
∵BE⊥直线CD,
∴∠FEC=90°,
∴∠F+∠DCA=90°.
∵∠BAC=90°,
∴∠FAB=90°=∠DAC.
∴∠F+∠FBA=90°,
∴∠FBA=∠DCA.在△FAB和△DAC中,$\left\{\begin{array}{l} ∠FAB=∠DAC,\\ AB=AC,\\ ∠FBA=∠DCA,\end{array}\right. $$\therefore \triangle FAB\cong \triangle DAC(ASA)$,$\therefore DA=FA$.②由①知$FA=DA$,$\therefore AB=AD+BD=FA+BD$.
(2)解:$AB=FA-BD$.所画图形如图所示.证明:
∵BE⊥直线CD,$\therefore ∠FED=90^{\circ }$,$\therefore ∠F+∠DCA=90^{\circ }$.$\because ∠BAC=90^{\circ }$,$\therefore ∠FAB=90^{\circ }=∠DAC$.$\therefore ∠F+∠FBA=90^{\circ }$,$\therefore ∠FBA=∠DCA$.在△FAB和△DAC中,$\left\{\begin{array}{l} ∠FAB=∠DAC,\\ AB=AC,\\ ∠FBA=∠DCA,\end{array}\right. $$\therefore \triangle FAB\cong \triangle DAC(ASA)$,$\therefore FA=DA$,$\therefore AB=AD-BD=FA-BD$.
查看更多完整答案,请扫码查看


