第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9.[2024·山西中考]一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力$F_{1}$的方向与斜面垂直,摩擦力$F_{2}$的方向与斜面平行.若斜面的坡角$α=25^{\circ }$,则摩擦力$F_{2}$与重力G方向的夹角β的度数为(
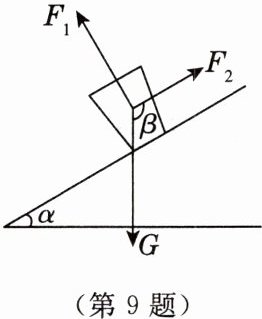
A.$155^{\circ }$
B.$125^{\circ }$
C.$115^{\circ }$
D.$65^{\circ }$
C
)
A.$155^{\circ }$
B.$125^{\circ }$
C.$115^{\circ }$
D.$65^{\circ }$
答案:
解:
过重力G的作用点作竖直向下的直线,过摩擦力F₂的作用点作沿斜面向上的直线(与斜面平行)。
因为斜面坡角α=25°,重力方向竖直向下,支持力F₁垂直于斜面,所以重力G与支持力F₁的夹角为α=25°(直角三角形两锐角互余)。
又因为摩擦力F₂平行于斜面,支持力F₁垂直于斜面,所以F₁与F₂的夹角为90°。
因此,摩擦力F₂与重力G方向的夹角β=90°+25°=115°。
答案:C
过重力G的作用点作竖直向下的直线,过摩擦力F₂的作用点作沿斜面向上的直线(与斜面平行)。
因为斜面坡角α=25°,重力方向竖直向下,支持力F₁垂直于斜面,所以重力G与支持力F₁的夹角为α=25°(直角三角形两锐角互余)。
又因为摩擦力F₂平行于斜面,支持力F₁垂直于斜面,所以F₁与F₂的夹角为90°。
因此,摩擦力F₂与重力G方向的夹角β=90°+25°=115°。
答案:C
10.[2025年1月淮北期末]在$△ABC$中,$∠A= 50^{\circ },∠B= 20^{\circ }$,点D在边AB上,连接CD,若$△ACD$为直角三角形,则$∠BCD$的度数为
$70°$或$20°$
.
答案:
【解析】:
本题主要考查三角形内角和定理的推论,即三角形内角和为$180^\circ$。
首先,我们已知在$\bigtriangleup ABC$中,$\angle A = 50^\circ$,$\angle B = 20^\circ$。
根据三角形内角和定理,我们可以求出$\angle ACB$:
$\angle ACB = 180^\circ - \angle A - \angle B = 180^\circ - 50^\circ - 20^\circ = 110^\circ$,
接下来,我们考虑$\bigtriangleup ACD$为直角三角形的情况。
当$\angle ADC = 90^\circ$时:
我们可以利用三角形内角和定理求出$\angle ACD$:
$\angle ACD = 180^\circ - \angle A - \angle ADC = 180^\circ - 50^\circ - 90^\circ = 40^\circ$,
然后,我们可以求出$\angle BCD$:
$\angle BCD = \angle ACB - \angle ACD = 110^\circ - 40^\circ = 70^\circ$,
当$\angle ADC$不是直角,而是$\angle ADC$所对其他内角的角为直角时,即$\angle CAD = 90^\circ$或$\angle ACD = 90^\circ$时,
由于$\angle A = 50^\circ$,显然$\angle CAD$不可能为$90^\circ$,
当$\angle ACD = 90^\circ$时,我们可以直接求出$\angle BCD$:
$\angle BCD = \angle ACB - \angle ACD = 110^\circ - 90^\circ = 20^\circ$,
综上所述,本题答案为:$70^\circ$或$20^\circ$。
【答案】:
$70^\circ$或$20^\circ$。
本题主要考查三角形内角和定理的推论,即三角形内角和为$180^\circ$。
首先,我们已知在$\bigtriangleup ABC$中,$\angle A = 50^\circ$,$\angle B = 20^\circ$。
根据三角形内角和定理,我们可以求出$\angle ACB$:
$\angle ACB = 180^\circ - \angle A - \angle B = 180^\circ - 50^\circ - 20^\circ = 110^\circ$,
接下来,我们考虑$\bigtriangleup ACD$为直角三角形的情况。
当$\angle ADC = 90^\circ$时:
我们可以利用三角形内角和定理求出$\angle ACD$:
$\angle ACD = 180^\circ - \angle A - \angle ADC = 180^\circ - 50^\circ - 90^\circ = 40^\circ$,
然后,我们可以求出$\angle BCD$:
$\angle BCD = \angle ACB - \angle ACD = 110^\circ - 40^\circ = 70^\circ$,
当$\angle ADC$不是直角,而是$\angle ADC$所对其他内角的角为直角时,即$\angle CAD = 90^\circ$或$\angle ACD = 90^\circ$时,
由于$\angle A = 50^\circ$,显然$\angle CAD$不可能为$90^\circ$,
当$\angle ACD = 90^\circ$时,我们可以直接求出$\angle BCD$:
$\angle BCD = \angle ACB - \angle ACD = 110^\circ - 90^\circ = 20^\circ$,
综上所述,本题答案为:$70^\circ$或$20^\circ$。
【答案】:
$70^\circ$或$20^\circ$。
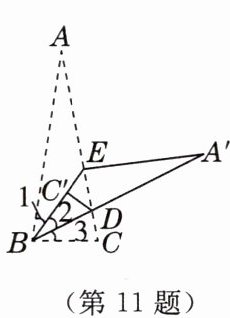
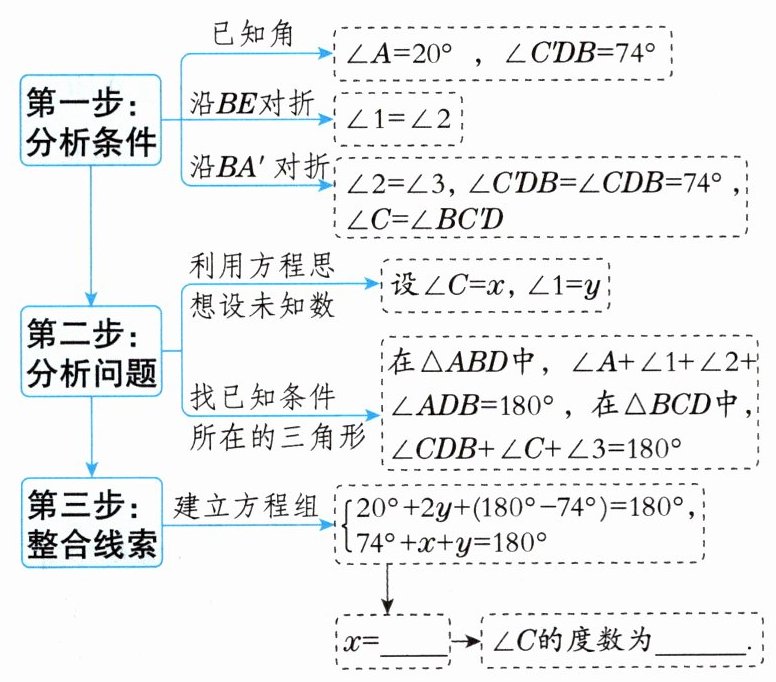
11.思维可视化如图,在$△ABC$中,$∠A= 20^{\circ }$,沿BE对折此三角形,又沿$BA'$再一次对折,使点C落在BE上的点$C'$处,此时$∠C'DB= 74^{\circ }$,如何求原三角形中$∠C$的度数?
思维过程

思维过程

答案:
解:设$∠C = x$,$∠1 = y$。由折叠性质得:$∠1 = ∠2 = y$,$∠2 = ∠3 = y$,$∠CDB = 74^{\circ}$。在$\triangle ABD$中,$∠ADB = 180^{\circ}-∠CDB = 180^{\circ}-74^{\circ}=106^{\circ}$,根据三角形内角和定理有:$∠A + ∠1 + ∠2 + ∠ADB = 180^{\circ}$,即$20^{\circ}+y + y + 106^{\circ}=180^{\circ}$,解得$2y = 54^{\circ}$,$y = 27^{\circ}$。在$\triangle BCD$中,根据三角形内角和定理有:$∠CDB + ∠C + ∠3 = 180^{\circ}$,即$74^{\circ}+x + y = 180^{\circ}$,将$y = 27^{\circ}$代入得$74^{\circ}+x + 27^{\circ}=180^{\circ}$,解得$x = 79^{\circ}$。$x = 79^{\circ}$→$∠C$的度数为$79^{\circ}$。$79^{\circ}$;$79^{\circ}$
12.如图,在$△ABC$中,AE平分$∠BAC,∠B= 26^{\circ },∠C= 64^{\circ }$.
(1)求$∠CAE$的度数;
(2)若$AD⊥BC$于点D,$∠ADF= 71^{\circ }$,试说明:$△ADF$是直角三角形.
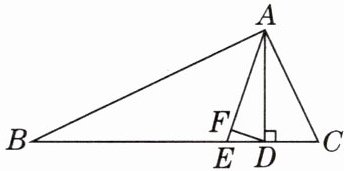
(1)求$∠CAE$的度数;
(2)若$AD⊥BC$于点D,$∠ADF= 71^{\circ }$,试说明:$△ADF$是直角三角形.

答案:
解:
(1)$∠CAE=45^{\circ }.$
(2)$\because AD⊥BC,\therefore △ACD$为直角三角形. $\because ∠C=64^{\circ },\therefore ∠DAC=90^{\circ }-∠C=26^{\circ }.$ $\because ∠CAE=45^{\circ },\therefore ∠DAF=∠CAE-∠DAC=19^{\circ }.$ $\because ∠ADF=71^{\circ },\therefore ∠ADF+∠DAF=90^{\circ },$ $\therefore ∠AFD=90^{\circ },\therefore △ADF$是直角三角形.
(1)$∠CAE=45^{\circ }.$
(2)$\because AD⊥BC,\therefore △ACD$为直角三角形. $\because ∠C=64^{\circ },\therefore ∠DAC=90^{\circ }-∠C=26^{\circ }.$ $\because ∠CAE=45^{\circ },\therefore ∠DAF=∠CAE-∠DAC=19^{\circ }.$ $\because ∠ADF=71^{\circ },\therefore ∠ADF+∠DAF=90^{\circ },$ $\therefore ∠AFD=90^{\circ },\therefore △ADF$是直角三角形.
13.推理能力规定:一条直线将三角形分割为两个图形,若其中一个新三角形与原三角形有两个角分别相等,则称这条直线为原三角形的恰巧线.例如:如图①,在$△ABC$中,直线DE将$△ABC$分割为两个图形,若新三角形ADE与原三角形ABC有$∠A= ∠A,∠ADE= ∠B$,则称直线DE为$△ABC$的恰巧线.
(1)在$△ABC$中,$∠A= 50^{\circ },∠B= 70^{\circ }$,点D,E分别在AB,AC边上(不与端点重合),若直线DE是$△ABC$的恰巧线,则$∠AED$的度数为
(2)如图②,在$△ABC$中,$∠ACB= 90^{\circ },CD⊥AB$,垂足为D,直线BE是$△ABC$的恰巧线,分别交AC于点E,交CD于点F,连接DE,且$∠A= ∠ADE$.求证:直线EF是$△CDE$的恰巧线.
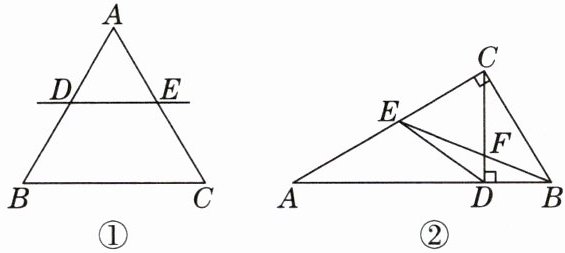
(1)在$△ABC$中,$∠A= 50^{\circ },∠B= 70^{\circ }$,点D,E分别在AB,AC边上(不与端点重合),若直线DE是$△ABC$的恰巧线,则$∠AED$的度数为
$60^{\circ }$或$70^{\circ }$
.(2)如图②,在$△ABC$中,$∠ACB= 90^{\circ },CD⊥AB$,垂足为D,直线BE是$△ABC$的恰巧线,分别交AC于点E,交CD于点F,连接DE,且$∠A= ∠ADE$.求证:直线EF是$△CDE$的恰巧线.

证明:∵直线 BE 是$△ABC$的恰巧线, $\therefore ∠CBE=∠A,\therefore ∠CEF=90^{\circ }-∠CBE=90^{\circ }-∠A.$ $\because ∠A=∠ADE,$ $\therefore ∠CEF=90^{\circ }-∠ADE=∠CDE.$ 而$∠ECF=∠DCE$,∴直线 EF 是$△CDE$的恰巧线.
答案:
13.
(1)$60^{\circ }$或$70^{\circ }$
(2)证明:
∵直线 BE 是$△ABC$的恰巧线, $\therefore ∠CBE=∠A,\therefore ∠CEF=90^{\circ }-∠CBE=90^{\circ }-∠A.$ $\because ∠A=∠ADE,$ $\therefore ∠CEF=90^{\circ }-∠ADE=∠CDE.$ 而$∠ECF=∠DCE$,
∴直线 EF 是$△CDE$的恰巧线.
(1)$60^{\circ }$或$70^{\circ }$
(2)证明:
∵直线 BE 是$△ABC$的恰巧线, $\therefore ∠CBE=∠A,\therefore ∠CEF=90^{\circ }-∠CBE=90^{\circ }-∠A.$ $\because ∠A=∠ADE,$ $\therefore ∠CEF=90^{\circ }-∠ADE=∠CDE.$ 而$∠ECF=∠DCE$,
∴直线 EF 是$△CDE$的恰巧线.
查看更多完整答案,请扫码查看


