第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1.三角形按边分类:
三角形等腰 (底边和腰不相等的等腰三角形
{
{
三角形等边三角形
2.三角形的三边关系:
三角形中任意(较短)两边的和
三边.
三角形中
即两边之差<第三边<两边之和.
不等边三角形
三角形等腰 (底边和腰不相等的等腰三角形
{
{
三角形等边三角形
2.三角形的三边关系:
三角形中任意(较短)两边的和
大于
第三边.
三角形中
任意两边的差
小于第三边.即两边之差<第三边<两边之和.
答案:
1. 不等边三角形
2. 大于;任意两边的差
2. 大于;任意两边的差
1.[2025.阜阳月考]下面是用三根火柴组成的图形,其中符合三角形概念的是 (
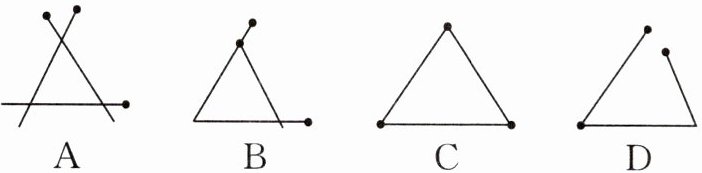
C
)
答案:
【解析】:
根据三角形的定义,三角形是由不在同一条直线上的三条线段首尾顺次相接组成的图形。
选项A中,三根火柴没有首尾顺次相接,不能组成三角形。
选项B中,三根火柴没有首尾顺次相接,不能组成三角形。
选项C中,三根火柴首尾顺次相接,符合三角形的概念。
选项D中,有两根火柴在同一条直线上,不能组成三角形。
【答案】:C
根据三角形的定义,三角形是由不在同一条直线上的三条线段首尾顺次相接组成的图形。
选项A中,三根火柴没有首尾顺次相接,不能组成三角形。
选项B中,三根火柴没有首尾顺次相接,不能组成三角形。
选项C中,三根火柴首尾顺次相接,符合三角形的概念。
选项D中,有两根火柴在同一条直线上,不能组成三角形。
【答案】:C
2.题练透根据下图填空:
(1)图中有
的三角形为
三角形为
(2)在△ABD中,顶点分别是
∠BAD所对的边是
角是
(3)∠B是△
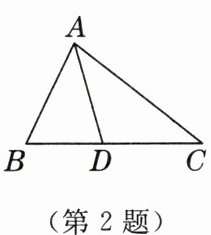
(1)图中有
5
个三角形,其中以AD为边的三角形为
△ABD,△ADC
,以点C为顶点的三角形为
△ACD,△BCD,△ABC
;(2)在△ABD中,顶点分别是
A,B,D
,∠BAD所对的边是
BD
,边AB所对的角是
∠ADB
;(3)∠B是△
ABD
和△ABC
的内角.
答案:
【解析】:
本题主要考查对三角形相关概念的理解,包括三角形的计数、边的识别、顶点的确定以及内角的判断等。
(1)
计数三角形个数时,按照一定顺序不重不漏地数。
以$AD$为边的三角形,就是看哪些三角形包含边$AD$。
以点$C$为顶点的三角形,就是找顶点为$C$的三角形。
(2)
对于$\triangle ABD$,明确其顶点的定义,即三角形三个端点。
$\angle BAD$所对的边,就是与$\angle BAD$相对的边。
边$AB$所对的角,就是与边$AB$相对的角。
(3)
判断$\angle B$是哪个三角形的内角,就是看哪些三角形包含$\angle B$。
【答案】:
(1) 图中有$5$个三角形,其中以$AD$为边的三角形为$\triangle ABD$,$\triangle ADC$;以点$C$为顶点的三角形为$\triangle ACD$,$\triangle BCD$,$\triangle ABC$。
(2) 在$\triangle ABD$中,顶点分别是$A$,$B$,$D$;$\angle BAD$所对的边是$BD$;边$AB$所对的角是$\angle ADB$。
(3) $\angle B$是$\triangle ABD$和$\triangle ABC$的内角。
本题主要考查对三角形相关概念的理解,包括三角形的计数、边的识别、顶点的确定以及内角的判断等。
(1)
计数三角形个数时,按照一定顺序不重不漏地数。
以$AD$为边的三角形,就是看哪些三角形包含边$AD$。
以点$C$为顶点的三角形,就是找顶点为$C$的三角形。
(2)
对于$\triangle ABD$,明确其顶点的定义,即三角形三个端点。
$\angle BAD$所对的边,就是与$\angle BAD$相对的边。
边$AB$所对的角,就是与边$AB$相对的角。
(3)
判断$\angle B$是哪个三角形的内角,就是看哪些三角形包含$\angle B$。
【答案】:
(1) 图中有$5$个三角形,其中以$AD$为边的三角形为$\triangle ABD$,$\triangle ADC$;以点$C$为顶点的三角形为$\triangle ACD$,$\triangle BCD$,$\triangle ABC$。
(2) 在$\triangle ABD$中,顶点分别是$A$,$B$,$D$;$\angle BAD$所对的边是$BD$;边$AB$所对的角是$\angle ADB$。
(3) $\angle B$是$\triangle ABD$和$\triangle ABC$的内角。
3.三角形按边的相等关系分类可用如图所示的集合来表示,则图中M,N分别表示的三角形是 (
A.等边三角形、等腰三角形
B.等腰三角形、等边三角形
C.锐角三角形、等腰三角形
D.等腰三角形、锐角三角形
B
)A.等边三角形、等腰三角形
B.等腰三角形、等边三角形
C.锐角三角形、等腰三角形
D.等腰三角形、锐角三角形
答案:
【解析】:
本题主要考察三角形按边的相等关系的分类及集合表示。
首先,需要明确三角形按边的相等关系可以分为等边三角形、等腰三角形和不等边三角形。
等边三角形:三边都相等的三角形。
等腰三角形:有两边相等的三角形。
不等边三角形:三边都不相等的三角形。
从集合的角度来看,等腰三角形包含了等边三角形,因为等边三角形是特殊的等腰三角形(即三边都相等的等腰三角形)。
因此,在集合表示中,等边三角形应该是等腰三角形的一个子集。
根据这个逻辑,可以判断图中M和N的位置:
M表示的是包含等边三角形的更大集合,即等腰三角形。
N表示的是等腰三角形中的一个特殊子集,即等边三角形。
对比选项:
A. 等边三角形、等腰三角形(顺序错误)
B. 等腰三角形、等边三角形(顺序正确)
C. 锐角三角形、等腰三角形(与题目要求的边的相等关系分类不符)
D. 等腰三角形、锐角三角形(与题目要求的边的相等关系分类不符)
因此,正确答案是B。
【答案】:
B
本题主要考察三角形按边的相等关系的分类及集合表示。
首先,需要明确三角形按边的相等关系可以分为等边三角形、等腰三角形和不等边三角形。
等边三角形:三边都相等的三角形。
等腰三角形:有两边相等的三角形。
不等边三角形:三边都不相等的三角形。
从集合的角度来看,等腰三角形包含了等边三角形,因为等边三角形是特殊的等腰三角形(即三边都相等的等腰三角形)。
因此,在集合表示中,等边三角形应该是等腰三角形的一个子集。
根据这个逻辑,可以判断图中M和N的位置:
M表示的是包含等边三角形的更大集合,即等腰三角形。
N表示的是等腰三角形中的一个特殊子集,即等边三角形。
对比选项:
A. 等边三角形、等腰三角形(顺序错误)
B. 等腰三角形、等边三角形(顺序正确)
C. 锐角三角形、等腰三角形(与题目要求的边的相等关系分类不符)
D. 等腰三角形、锐角三角形(与题目要求的边的相等关系分类不符)
因此,正确答案是B。
【答案】:
B
4.[知识初练]如图,在△ABC中,AB十AC
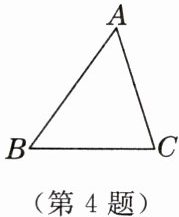
>
BC,AB-AC<
BC.(填“>"“<"或“=”)
答案:
【解析】:
本题考查三角形三边关系,即三角形任意两边之和大于第三边,任意两边之差小于第三边。
对于$AB + AC$与$BC$的关系,根据三角形三边关系“三角形任意两边之和大于第三边”,在$\triangle ABC$中,$AB$与$AC$是两边,$BC$是第三边,所以$AB + AC\gt BC$。
对于$AB - AC$与$BC$的关系,根据三角形三边关系“三角形任意两边之差小于第三边”,在$\triangle ABC$中,$AB$与$AC$是两边,$BC$是第三边,所以$AB - AC\lt BC$。
【答案】:
$>$;$<$
本题考查三角形三边关系,即三角形任意两边之和大于第三边,任意两边之差小于第三边。
对于$AB + AC$与$BC$的关系,根据三角形三边关系“三角形任意两边之和大于第三边”,在$\triangle ABC$中,$AB$与$AC$是两边,$BC$是第三边,所以$AB + AC\gt BC$。
对于$AB - AC$与$BC$的关系,根据三角形三边关系“三角形任意两边之差小于第三边”,在$\triangle ABC$中,$AB$与$AC$是两边,$BC$是第三边,所以$AB - AC\lt BC$。
【答案】:
$>$;$<$
5.[2025年1月芜湖期末]在下列长度的三条线段中,能组成三角形的是 (
A.3cm,5cm,8cm
B.8cm,8cm,18cm
C.1cm,1cm,1cm
D.3cm,4cm,8cm
C
)A.3cm,5cm,8cm
B.8cm,8cm,18cm
C.1cm,1cm,1cm
D.3cm,4cm,8cm
答案:
【解析】:
本题主要考察三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。这是判断三条线段能否组成三角形的关键条件。
A选项:$3\text{cm} + 5\text{cm} = 8\text{cm}$,两边之和等于第三边,所以不能组成三角形。
B选项:$8\text{cm} + 8\text{cm} = 16\text{cm} \lt 18\text{cm}$,两边之和小于第三边,所以不能组成三角形。
C选项:$1\text{cm} + 1\text{cm} = 2\text{cm} \gt 1\text{cm}$,且$1\text{cm} - 1\text{cm} = 0\text{cm} \lt 1\text{cm}$,满足三角形的三边关系,所以能组成三角形。
D选项:$3\text{cm} + 4\text{cm} = 7\text{cm} \lt 8\text{cm}$,两边之和小于第三边,所以不能组成三角形。
综上所述,只有C选项的三条线段能组成三角形。
【答案】:
C
本题主要考察三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边。这是判断三条线段能否组成三角形的关键条件。
A选项:$3\text{cm} + 5\text{cm} = 8\text{cm}$,两边之和等于第三边,所以不能组成三角形。
B选项:$8\text{cm} + 8\text{cm} = 16\text{cm} \lt 18\text{cm}$,两边之和小于第三边,所以不能组成三角形。
C选项:$1\text{cm} + 1\text{cm} = 2\text{cm} \gt 1\text{cm}$,且$1\text{cm} - 1\text{cm} = 0\text{cm} \lt 1\text{cm}$,满足三角形的三边关系,所以能组成三角形。
D选项:$3\text{cm} + 4\text{cm} = 7\text{cm} \lt 8\text{cm}$,两边之和小于第三边,所以不能组成三角形。
综上所述,只有C选项的三条线段能组成三角形。
【答案】:
C
6.[25实绍拟]一款可折叠晾衣架的示意图
如图所示,支架OP= OQ= 30cm(接头处的
长度忽略不计),则点P,Q之间的距离可以是
(
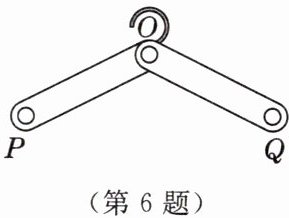
A.50cm
B.65cm
C.70cm
D.80cm
如图所示,支架OP= OQ= 30cm(接头处的
长度忽略不计),则点P,Q之间的距离可以是
(
A
)
A.50cm
B.65cm
C.70cm
D.80cm
答案:
【解析】:
本题可根据三角形三边关系来确定点$P$,$Q$之间的距离范围,进而判断选项。
步骤一:分析$OP$,$OQ$与$PQ$构成的三角形
在可折叠晾衣架的示意图中,$OP$,$OQ$和$PQ$构成了一个三角形(当$P$,$O$,$Q$三点不共线时),已知$OP = OQ = 30cm$。
步骤二:根据三角形三边关系确定$PQ$的取值范围
根据三角形三边关系“两边之和大于第三边,两边之差小于第三边”,在$\triangle OPQ$中,$OP$与$OQ$的差小于$PQ$,$OP$与$OQ$的和大于$PQ$,即$\vert OP - OQ\vert\lt PQ\lt OP + OQ$。
将$OP = OQ = 30cm$代入可得:$\vert30 - 30\vert\lt PQ\lt 30 + 30$,也就是$0\lt PQ\lt 60cm$。
当$P$,$O$,$Q$三点共线时,$PQ$的长度为$OP + OQ = 30 + 30 = 60cm$或$\vert OP - OQ\vert = \vert30 - 30\vert = 0cm$(舍去这种情况),所以$PQ$的取值范围是$0\lt PQ\leqslant 60cm$。
步骤三:逐一分析选项
选项A:$50cm$在$0\lt PQ\leqslant 60cm$这个范围内,该选项正确。
选项B:$65cm\gt 60cm$,不在$0\lt PQ\leqslant 60cm$这个范围内,该选项错误。
选项C:$70cm\gt 60cm$,不在$0\lt PQ\leqslant 60cm$这个范围内,该选项错误。
选项D:$80cm\gt 60cm$,不在$0\lt PQ\leqslant 60cm$这个范围内,该选项错误。
【答案】:A
本题可根据三角形三边关系来确定点$P$,$Q$之间的距离范围,进而判断选项。
步骤一:分析$OP$,$OQ$与$PQ$构成的三角形
在可折叠晾衣架的示意图中,$OP$,$OQ$和$PQ$构成了一个三角形(当$P$,$O$,$Q$三点不共线时),已知$OP = OQ = 30cm$。
步骤二:根据三角形三边关系确定$PQ$的取值范围
根据三角形三边关系“两边之和大于第三边,两边之差小于第三边”,在$\triangle OPQ$中,$OP$与$OQ$的差小于$PQ$,$OP$与$OQ$的和大于$PQ$,即$\vert OP - OQ\vert\lt PQ\lt OP + OQ$。
将$OP = OQ = 30cm$代入可得:$\vert30 - 30\vert\lt PQ\lt 30 + 30$,也就是$0\lt PQ\lt 60cm$。
当$P$,$O$,$Q$三点共线时,$PQ$的长度为$OP + OQ = 30 + 30 = 60cm$或$\vert OP - OQ\vert = \vert30 - 30\vert = 0cm$(舍去这种情况),所以$PQ$的取值范围是$0\lt PQ\leqslant 60cm$。
步骤三:逐一分析选项
选项A:$50cm$在$0\lt PQ\leqslant 60cm$这个范围内,该选项正确。
选项B:$65cm\gt 60cm$,不在$0\lt PQ\leqslant 60cm$这个范围内,该选项错误。
选项C:$70cm\gt 60cm$,不在$0\lt PQ\leqslant 60cm$这个范围内,该选项错误。
选项D:$80cm\gt 60cm$,不在$0\lt PQ\leqslant 60cm$这个范围内,该选项错误。
【答案】:A
7.已知三角形两边的长分别是2cm和7cm,若第三边的长为奇数(单位:cm),则这个三角形第三边的长为
7
cm.
答案:
【解析】:
本题主要考查三角形的三边关系。
根据三角形的性质,任意两边之和大于第三边,任意两边之差小于第三边。
设第三边为$x$,则有:
$7 - 2 < x < 7 + 2$
即
$5 < x < 9$
由于题目要求第三边的长为奇数,那么在5到9之间的奇数有7。
因此,第三边的长为7cm。
【答案】:
7
本题主要考查三角形的三边关系。
根据三角形的性质,任意两边之和大于第三边,任意两边之差小于第三边。
设第三边为$x$,则有:
$7 - 2 < x < 7 + 2$
即
$5 < x < 9$
由于题目要求第三边的长为奇数,那么在5到9之间的奇数有7。
因此,第三边的长为7cm。
【答案】:
7
8.易错题已知等腰三角形的两边长分别为3cm, 8cm,则该等腰三角形的周长是
[变式题]若等腰三角形ABC的周长为14,腰AB长为x,则x的取值范围为
19
cm.[变式题]若等腰三角形ABC的周长为14,腰AB长为x,则x的取值范围为
3.5<x<7
.
答案:
【解析】:
本题主要考查等腰三角形的性质以及三角形三边关系。
对于第一个问题,需要判断等腰三角形的可能边长组合,并计算周长。
由于等腰三角形的两腰相等,所以可能的边长组合为3cm,3cm,8cm或3cm,8cm,8cm。
根据三角形的三边关系,任意两边之和大于第三边,所以3cm,3cm,8cm不能构成三角形,而3cm,8cm,8cm可以构成三角形。
因此,等腰三角形的周长为$3+8+8=19cm$。
对于第二个问题,需要根据等腰三角形的周长和腰长,求出腰长的取值范围。
设等腰三角形的底为$y$,则$2x+y=14$,从中解出$y=14-2x$。
根据三角形的三边关系,有$2x>y$且$y>0$,即$2x>14-2x$且$14-2x>0$。
解这个不等式组,得到$x$的取值范围。
【答案】:
19;$3.5 < x < 7$。
本题主要考查等腰三角形的性质以及三角形三边关系。
对于第一个问题,需要判断等腰三角形的可能边长组合,并计算周长。
由于等腰三角形的两腰相等,所以可能的边长组合为3cm,3cm,8cm或3cm,8cm,8cm。
根据三角形的三边关系,任意两边之和大于第三边,所以3cm,3cm,8cm不能构成三角形,而3cm,8cm,8cm可以构成三角形。
因此,等腰三角形的周长为$3+8+8=19cm$。
对于第二个问题,需要根据等腰三角形的周长和腰长,求出腰长的取值范围。
设等腰三角形的底为$y$,则$2x+y=14$,从中解出$y=14-2x$。
根据三角形的三边关系,有$2x>y$且$y>0$,即$2x>14-2x$且$14-2x>0$。
解这个不等式组,得到$x$的取值范围。
【答案】:
19;$3.5 < x < 7$。
查看更多完整答案,请扫码查看


