《2025年点拨训练八年级数学上册沪科版安徽专版》

10. 下面给出的四个三角形都有一部分被遮挡住了,其中不能判断三角形类型的是(C)

答案： 【解析】：由题可知，
选项A，图中露出了两个锐角，根据三角形内角和为$180^\circ$，可求出被遮挡的角也是锐角，所以这个三角形是锐角三角形，可以判断其类型。
选项B，图中露出了一个直角和一个锐角，根据三角形内角和为$180^\circ$，可求出被遮挡的角是锐角，所以这个三角形是直角三角形，可以判断其类型。
选项C，图中只露出了一个锐角，仅根据这一个锐角，无法确定其他两个角的度数情况，也就不能判断这个三角形的类型。
选项D，图中露出了一个钝角，根据三角形中有一个角是钝角的三角形是钝角三角形，所以这个三角形是钝角三角形，可以判断其类型。
【答案】：C

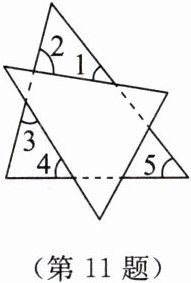
11. [2025年1月安庆期末]将两张三角形纸片按如图所示摆放,量得$∠1 + ∠2 + ∠3 + ∠4 = 220^{\circ}$,则$∠5$的度数为(B)

A.$30^{\circ}$
B.$40^{\circ}$
C.$45^{\circ}$
D.$50^{\circ}$

答案： 【解析】：本题可根据平角的定义以及三角形内角和定理来求解$\angle5$的度数。
步骤一：根据平角的定义得到$\angle1$、$\angle2$与三角形另外两个内角和的关系
观察图形可知，$\angle1$与它相邻的三角形的一个内角组成一个平角，$\angle2$与它相邻的三角形的另一个内角组成一个平角。
因为平角为$180^{\circ}$，所以$\angle1 + \angle2 +$与$\angle1$相邻的三角形的内角$+$与$\angle2$相邻的三角形的内角$= 180^{\circ}+180^{\circ}=360^{\circ}$。
步骤二：根据已知条件求出$\angle1$、$\angle2$与$\angle3$、$\angle4$组成角的度数
已知$\angle1 + \angle2 + \angle3 + \angle4 = 220^{\circ}$。
步骤三：求出$\angle5$所在三角形的另外两个内角和
用$\angle1 + \angle2 +$与$\angle1$相邻的三角形的内角$+$与$\angle2$相邻的三角形的内角$-\left(\angle1 + \angle2 + \angle3 + \angle4\right)$，即$360^{\circ}-220^{\circ}=140^{\circ}$，得到$\angle5$所在三角形的另外两个内角和为$140^{\circ}$。
步骤四：根据三角形内角和定理求出$\angle5$的度数
因为三角形内角和为$180^{\circ}$，设$\angle5$所在三角形的三个内角分别为$\angle5$、$\angle A$、$\angle B$，则$\angle5 + \angle A + \angle B = 180^{\circ}$，而$\angle A + \angle B = 140^{\circ}$，所以$\angle5 = 180^{\circ}-(\angle A + \angle B)=180^{\circ}-140^{\circ}=40^{\circ}$。
【答案】：B

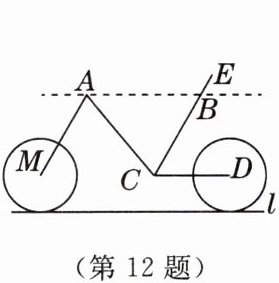
12. 立德树人·关注生活2025年1月合肥期末如图是某品牌共享单车放在水平地面的示意图,其中$AB,CD都与地面l$平行,$∠BCD = 60^{\circ},∠BAC = 50^{\circ}$,当$∠MAC$为70$^{\circ}$时,$AM// BE$.

答案： 70

13. 创新题·新题型当三角形中一个内角$∠α$是另一个内角的一半时,我们称此三角形为“特征三角形”,其中$∠α$称为“特征角”.如果一个“特征三角形”恰好是直角三角形,求这个“特征角”的度数.

答案： 解：设特征角为∠α，则另一个内角为2∠α。
情况一：∠α和2∠α均为锐角。
∠α + 2∠α + 90° = 180°
3∠α = 90°
∠α = 30°
情况二：2∠α为直角。
2∠α = 90°
∠α = 45°
情况三：∠α为直角，则2∠α = 180°，不符合三角形内角和定理，舍去。
综上，特征角的度数为30°或45°。

14. 中考趋势·探究建模将三角尺($\triangle MPN,∠MPN = 90^{\circ}$)放置在$\triangle ABC$上(点$P在\triangle ABC$内),如图①所示,三角尺的两边$PM,PN恰好分别经过点B$、点$C$,我们来研究$∠ABP与∠ACP$是否存在某种数量关系.
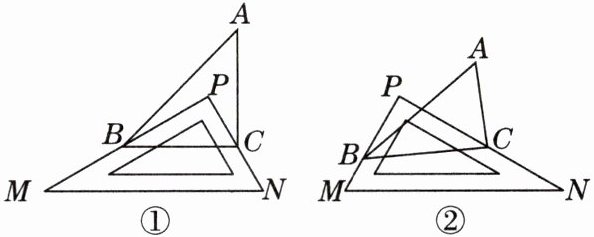
(1) 特例探究：$∠PBC + ∠PCB = $90$^{\circ}$,若$∠A = 50^{\circ}$,则$∠ABP + ∠ACP = $40$^{\circ}$；
(2) 类比探究：$∠ABP,∠ACP,∠A$之间的数量关系；
解：在△ABC中，∠ABC + ∠ACB = 180° - ∠A
在△PBC中，∠PBC + ∠PCB = 90°
∵∠ABC = ∠ABP + ∠PBC，∠ACB = ∠ACP + ∠PCB
∴(∠ABP + ∠PBC) + (∠ACP + ∠PCB) = 180° - ∠A
∴∠ABP + ∠ACP + (∠PBC + ∠PCB) = 180° - ∠A
∴∠ABP + ∠ACP + 90° = 180° - ∠A
∴∠ABP + ∠ACP = 90° - ∠A
(3) 变式探究：如图②所示,将图①中$\triangle ABC$的形状改变,同时改变三角尺的位置,使点$P在\triangle ABC$外,三角尺的两边$PM,PN仍恰好分别经过点B$、点$C$,探究$∠ABP,∠ACP,∠A$之间的数量关系.
解：在△ABC中，∠ABC + ∠ACB = 180° - ∠A
在△PBC中，∠PBC + ∠PCB = 90°
∵∠PBC = ∠ABC + ∠ABP，∠PCB = ∠ACB + ∠ACP
∴(∠ABC + ∠ABP) + (∠ACB + ∠ACP) = 90°
∴∠ABC + ∠ACB + ∠ABP + ∠ACP = 90°
∴(180° - ∠A) + ∠ABP + ∠ACP = 90°
∴∠ABP + ∠ACP = ∠A - 90°

答案：
(1) 90；40
(2) 解：在△ABC中，∠ABC + ∠ACB = 180° - ∠A
在△PBC中，∠PBC + ∠PCB = 90°
∵∠ABC = ∠ABP + ∠PBC，∠ACB = ∠ACP + ∠PCB
∴(∠ABP + ∠PBC) + (∠ACP + ∠PCB) = 180° - ∠A
∴∠ABP + ∠ACP + (∠PBC + ∠PCB) = 180° - ∠A
∴∠ABP + ∠ACP + 90° = 180° - ∠A
∴∠ABP + ∠ACP = 90° - ∠A
(3) 解：在△ABC中，∠ABC + ∠ACB = 180° - ∠A
在△PBC中，∠PBC + ∠PCB = 90°
∵∠PBC = ∠ABC + ∠ABP，∠PCB = ∠ACB + ∠ACP
∴(∠ABC + ∠ABP) + (∠ACB + ∠ACP) = 90°
∴∠ABC + ∠ACB + ∠ABP + ∠ACP = 90°
∴(180° - ∠A) + ∠ABP + ∠ACP = 90°
∴∠ABP + ∠ACP = ∠A - 90°