第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. [中考趋势·项目式学习 2024·吉林中考]某班同学分三个小组进行“板凳中的数学”的项目式学习研究,第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
如图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为$x$mm,凳面的宽度为$y$mm,记录如下:
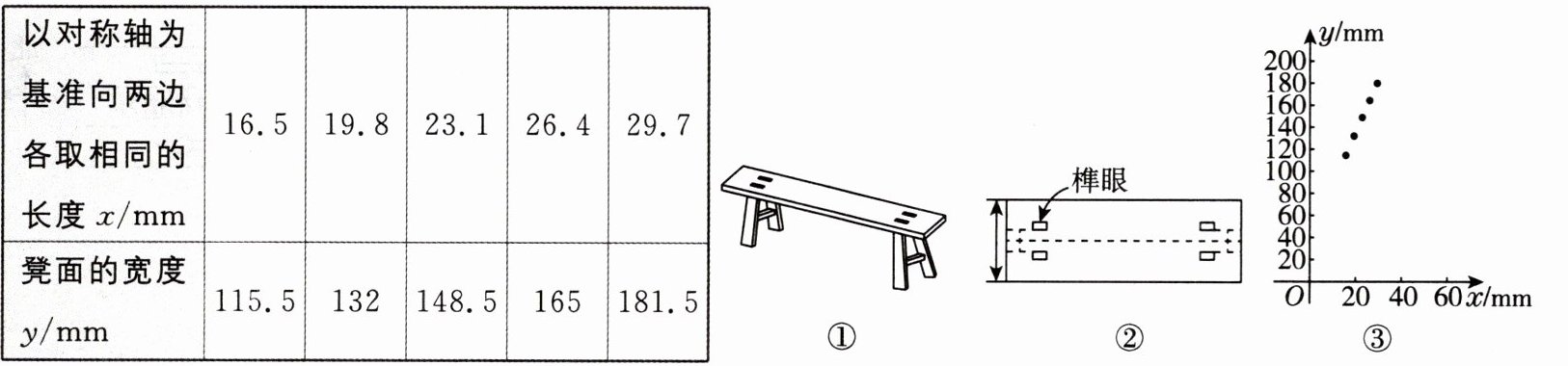
【分析数据】
如图③,小组根据表中$x$,$y$的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,说明理由.
(2)当凳面的宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?
【背景调查】
如图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为$x$mm,凳面的宽度为$y$mm,记录如下:

【分析数据】
如图③,小组根据表中$x$,$y$的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,说明理由.
(2)当凳面的宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?
答案:
1.解:
(1)在.设这条直线所对应的函数表达式为y=kx+b(k≠0),因为当x=16.5时,y=115.5,当x=23.1时,y=148.5,所以{16.5k+b=115.5,23.1k+b=148.5,解得{k=5,b=33,所以这条直线所对应的函数表达式为y=5x+33,经检验,其余点均在直线y=5x+33上,所以这些点在同一条直线上,这条直线所对应的函数表达式为y=5x+33.
(2)把y=213代入y=5x+33,得5x+33=213,解得x=36,所以当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度是36 mm.
(1)在.设这条直线所对应的函数表达式为y=kx+b(k≠0),因为当x=16.5时,y=115.5,当x=23.1时,y=148.5,所以{16.5k+b=115.5,23.1k+b=148.5,解得{k=5,b=33,所以这条直线所对应的函数表达式为y=5x+33,经检验,其余点均在直线y=5x+33上,所以这些点在同一条直线上,这条直线所对应的函数表达式为y=5x+33.
(2)把y=213代入y=5x+33,得5x+33=213,解得x=36,所以当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度是36 mm.
2. [中考趋势·探究建模 2025·天津模拟]某条东西方向道路双向共有三条车道,在早晚高峰时段经常出现拥堵现象,某数学小组对该路段的交通量(单位:辆/min)和时间进行了统计和分析,相应数据如下表所示,并发现交通量和时间的变化规律符合一次函数的特征,其中$y_{2}= -x+33$.

(1)求$y_{1}与x$之间的函数表达式;
(2)在13时时,通过计算判断$y_{1}与y_{2}$的大小关系;
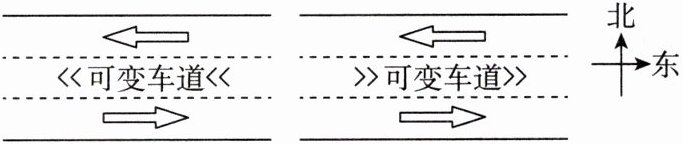
(3)如图,该小组建议引入“可变车道”系统以缓解交通拥堵,该系统将根据实时交通流量调整车道的行驶方向.单位时间内,双向交通总量为$v= y_{1}+y_{2}$,交通量较大的为$y$,经查阅资料得:当$y\geqslant \frac{2}{3}v$时,表明交通处于严重拥堵状态,需使可变车道行车方向与交通量较大的方向相同,以改善交通状况.该路段从8时至20时,请通过计算判断在严重拥堵时如何设置可变车道行车方向以缓解交通拥堵.

(1)求$y_{1}与x$之间的函数表达式;
(2)在13时时,通过计算判断$y_{1}与y_{2}$的大小关系;
(3)如图,该小组建议引入“可变车道”系统以缓解交通拥堵,该系统将根据实时交通流量调整车道的行驶方向.单位时间内,双向交通总量为$v= y_{1}+y_{2}$,交通量较大的为$y$,经查阅资料得:当$y\geqslant \frac{2}{3}v$时,表明交通处于严重拥堵状态,需使可变车道行车方向与交通量较大的方向相同,以改善交通状况.该路段从8时至20时,请通过计算判断在严重拥堵时如何设置可变车道行车方向以缓解交通拥堵.

答案:
2.解:
(1)y1与x之间的函数表达式为y1=2x-6.
(2)当x=13时,y1=2×13-6=20,y2=-13+33=20,所以y1与y2的大小关系为y1=y2.
(3)当2x-6>-x+33时,x>13.当-x+33>2x-6时,x<13.所以当8≤x≤13时,y=-x+33;当13<x≤20时,y=2x-6.v=y1+y2=x+27.当2x-6≥23(x+27)时,解得x≥18;当-x+33≥23(x+27)时,解得x≤9,所以8时至9时,可变车道的方向设置为自东向西;18时至20时,可变车道的方向设置为自西向东.
(1)y1与x之间的函数表达式为y1=2x-6.
(2)当x=13时,y1=2×13-6=20,y2=-13+33=20,所以y1与y2的大小关系为y1=y2.
(3)当2x-6>-x+33时,x>13.当-x+33>2x-6时,x<13.所以当8≤x≤13时,y=-x+33;当13<x≤20时,y=2x-6.v=y1+y2=x+27.当2x-6≥23(x+27)时,解得x≥18;当-x+33≥23(x+27)时,解得x≤9,所以8时至9时,可变车道的方向设置为自东向西;18时至20时,可变车道的方向设置为自西向东.
查看更多完整答案,请扫码查看


