《2025年点拨训练八年级数学上册沪科版安徽专版》

1.定理:三角形的内角和等于$180^{\circ }$.
2.推论1:直角三角形的两锐角互余.
3.推论2:有两个角互余的三角形是直角三角形.
1星题 基础题

答案： 1.$180^{\circ }$ 2.互余 3.互余

1.创新题·新题型阅读材料:为了证明“三角形的内角和是$180^{\circ }$”,林老师给出了如图所示四种作辅助线的方法,请回答下列问题:

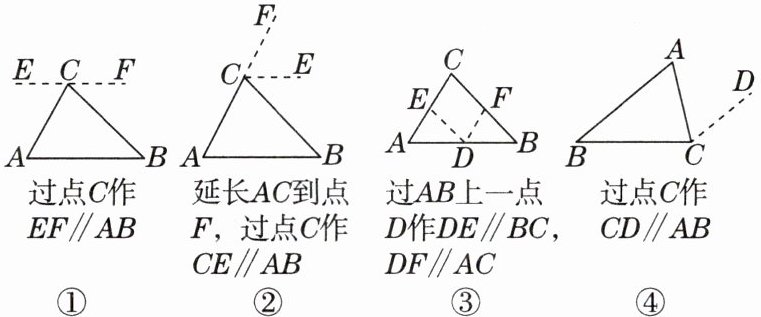
(1)图①②在证明三角形内角和定理的过程中应用的数学思想是(A)
A.转化思想
B.整体思想
C.方程思想
D.数形结合思想
(2)请选用③或④证明三角形的内角和为$180^{\circ }$.

答案： 【解析】：
(1)观察图①和图②，它们都是通过作辅助线将三角形的内角转化为平角或同旁内角，从而证明三角形的内角和为$180°$。这种将未知问题转化为已知问题的方法，是转化思想的体现。
因此，答案是A。
(2)选择图③进行证明。
证明：
由于$DE // BC$，
根据平行线的性质，同位角相等，
$\therefore \angle B = \angle EDB$（同位角），
$\because DF // AC$，
$\therefore \angle C = \angle FDB$（同位角），
又$\because \angle EDB + \angle A + \angle FDB = 180°$（平角的定义），
$\therefore \angle A + \angle B + \angle C = 180°$。
【答案】：
(1)A
(2)证明过程如上。

2.[知识初练]在$Rt△ABC$中,$∠C= 90^{\circ }$,则$∠A+∠B$的大小为(C)
A.$30^{\circ }$
B.$60^{\circ }$
C.$90^{\circ }$
D.$180^{\circ }$

答案： 【解析】：
题目考查了三角形内角和定理，即在任何三角形中，三个内角的和总是等于$180^{\circ }$。
在直角三角形$Rt△ABC$中，已知$∠C= 90^{\circ }$，根据三角形内角和定理，有$∠A+∠B+∠C= 180^{\circ }$。
由此可以推出$∠A+∠B= 180^{\circ }- 90^{\circ }= 90^{\circ }$。
【答案】：
C.$90^{\circ }$。

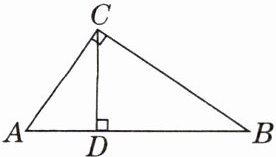
3.[2025年1月芜湖期末]如图,已知$AC⊥BC$于点C,$CD⊥AB$于点D,$∠A= 56^{\circ }$,则$∠DCB$的度数是$56^{\circ }$.

答案： 【解析】：本题主要考查直角三角形的性质。
因为$AC⊥BC$，
所以$\angle ACB=90^\circ$，
所以$\angle A+\angle B=90^\circ$。
因为$CD⊥AB$，
所以$\angle CDB=90^\circ$，
所以$\angle DCB+\angle B=90^\circ$。
因为$\angle A+\angle B=90^\circ$，$\angle DCB+\angle B=90^\circ$，
等量代换可得$\angle DCB=\angle A=56^\circ$。
【答案】：$56^\circ$

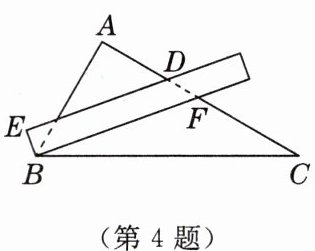
4.[2025·台州模拟]将一个含$30^{\circ }$角的直角三角板和一把等宽的直尺按如图所示的位置摆放,其中$∠C= 30^{\circ }$,若$∠ADE= 50^{\circ }$,则$∠FBC$的度数是20°.

答案： 证明：
∵直尺两边平行，
∴∠AED=∠ADE=50°（两直线平行，内错角相等）。
∵∠AED是△BEC的外角，
∴∠AED=∠C+∠EBC（三角形的一个外角等于与它不相邻的两个内角的和）。
∵∠C=30°，
∴∠EBC=∠AED-∠C=50°-30°=20°。
∵点F在BE上，
∴∠FBC=∠EBC=20°。
20°

5.[知识初练]在$△ABC$中,若$∠A+∠B= 90^{\circ }$,则$△ABC$一定是(B)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形

答案： 【解析】：
本题可根据三角形内角和定理以及已知条件$∠A + ∠B = 90^{\circ}$，求出$∠C$的度数，再根据三角形的分类来判断$\triangle ABC$的形状。
步骤一：根据三角形内角和定理求出$∠C$的度数
三角形内角和定理为：三角形的内角和等于$180^{\circ}$，即在$\triangle ABC$中，$∠A + ∠B + ∠C = 180^{\circ}$。
已知$∠A + ∠B = 90^{\circ}$，将其代入到$∠A + ∠B + ∠C = 180^{\circ}$中，可得$90^{\circ} + ∠C = 180^{\circ}$。
等式两边同时减去$90^{\circ}$，解得$∠C = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
步骤二：根据三角形的分类判断$\triangle ABC$的形状
三角形按角分类可分为：
锐角三角形：三个角都小于$90^{\circ}$的三角形。
直角三角形：有一个角等于$90^{\circ}$的三角形。
钝角三角形：有一个角大于$90^{\circ}$的三角形。
由于在$\triangle ABC$中，$∠C = 90^{\circ}$，满足直角三角形的定义，所以$\triangle ABC$一定是直角三角形。
【答案】：B

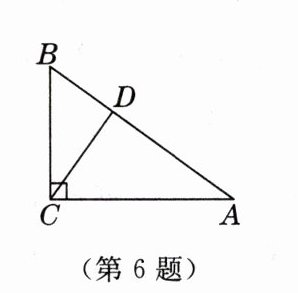
6.如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },∠A= ∠BCD$,则$△BDC$是直角三角形.

答案： 直角

7.[2025·合肥月考]如图,$AB// CD$,AC平分$∠BAD$,DB平分$∠ADC$,AC和DB交于点E.求证:$△ADE$是直角三角形.

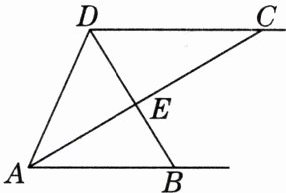
答案： 【解析】：本题可根据平行线的性质、角平分线的定义以及三角形内角和定理来证明$\triangle ADE$是直角三角形。
已知$AB// CD$，根据两直线平行，同旁内角互补，可得$\angle BAD + \angle ADC = 180^{\circ}$。
因为$AC$平分$\angle BAD$，$DB$平分$\angle ADC$，根据角平分线的定义，可知$\angle DAC=\frac{1}{2}\angle BAD$，$\angle ADB=\frac{1}{2}\angle ADC$。
在$\triangle ADE$中，根据三角形内角和定理$\angle DAE + \angle ADE + \angle AED = 180^{\circ}$，通过求出$\angle DAE + \angle ADE$的度数，进而求出$\angle AED$的度数，判断$\triangle ADE$的形状。
【答案】：
证明：
∵$AB// CD$，
∴$\angle BAD + \angle ADC = 180^{\circ}$（两直线平行，同旁内角互补）。
∵$AC$平分$\angle BAD$，$DB$平分$\angle ADC$，
∴$\angle DAC=\frac{1}{2}\angle BAD$，$\angle ADB=\frac{1}{2}\angle ADC$（角平分线的定义）。
∴$\angle DAC + \angle ADB=\frac{1}{2}(\angle BAD + \angle ADC)$。
把$\angle BAD + \angle ADC = 180^{\circ}$代入上式可得：
$\angle DAC + \angle ADB=\frac{1}{2}×180^{\circ}=90^{\circ}$。
在$\triangle ADE$中，根据三角形内角和定理$\angle DAE + \angle ADE + \angle AED = 180^{\circ}$，
则$\angle AED = 180^{\circ}-(\angle DAE + \angle ADE)$。
把$\angle DAC + \angle ADB = 90^{\circ}$（$\angle DAE=\angle DAC$，$\angle ADE=\angle ADB$）代入可得：
$\angle AED = 180^{\circ}- 90^{\circ}= 90^{\circ}$。
所以$\triangle ADE$是直角三角形。

8.[2025年1月合肥期末]有下列条件:①$∠A+∠C= ∠B$;②$∠A:∠B:∠C= 2:3:5$;③$∠A= ∠B= 2∠C$;④$∠A= ∠B= \frac {1}{2}∠C$,其中能确定$△ABC$是直角三角形的有(①②④)
A.1个
B.2个
C.3个
D.4个

答案： 【解析】：
本题主要考察三角形内角和定理及其推论的应用。
三角形内角和定理：三角形的三个内角之和等于180°。
接下来，我们逐一验证每个条件：
① 对于条件$∠A+∠C= ∠B$：
根据三角形内角和定理，我们有$∠A+∠B+∠C=180°$。
将$∠A+∠C= ∠B$代入上式，得到$2∠B=180°$，即$∠B=90°$。
因此，条件①能确定$△ABC$是直角三角形。
② 对于条件$∠A:∠B:∠C= 2:3:5$：
设$∠A=2x$，$∠B=3x$，$∠C=5x$。
根据三角形内角和定理，我们有$2x+3x+5x=180°$，解得$x=18°$。
因此，$∠C=5x=90°$。
所以，条件②也能确定$△ABC$是直角三角形。
③ 对于条件$∠A= ∠B= 2∠C$：
设$∠C=x$，则$∠A=∠B=2x$。
根据三角形内角和定理，我们有$x+2x+2x=180°$，解得$x=36°$。
因此，$∠A=∠B=72°$，$∠C=36°$。
没有90°的角，所以条件③不能确定$△ABC$是直角三角形。
④ 对于条件$∠A= ∠B= \frac {1}{2}∠C$：
设$∠A=∠B=x$，则$∠C=2x$。
根据三角形内角和定理，我们有$x+x+2x=180°$，解得$x=45°$。
因此，$∠C=2x=90°$。
所以，条件④也能确定$△ABC$是直角三角形。
综上所述，能确定$△ABC$是直角三角形的有①②④，共3个。
【答案】：
C