《2025年点拨训练八年级数学上册沪科版安徽专版》

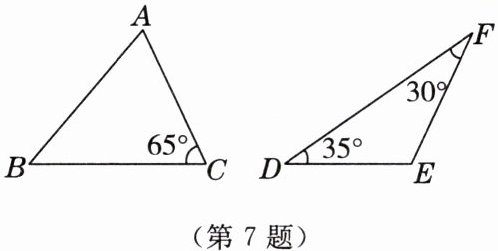
7. 如图,设$\triangle ABC中BC边上的高为h_{1}$,$\triangle DEF中DE边上的高为h_{2}$,若$AC = EF$,则下列结论中正确的是(B)

A.$h_{1}\lt h_{2}$
B.$h_{1}\gt h_{2}$
C.$h_{1}= h_{2}$
D.无法确定

答案： 解：在$\triangle ABC$中，$BC$边上的高$h_1 = AC \cdot \sin \angle ACB$。
在$\triangle DEF$中，$DE$边上的高$h_2 = EF \cdot \sin \angle FDE$。
已知$AC = EF$，$\angle ACB = 65^\circ$，$\angle FDE = 35^\circ$。
因为$\sin 65^\circ ＞ \sin 35^\circ$，所以$h_1 ＞ h_2$。
B

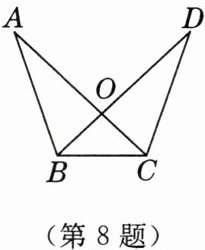
8. 如图,$\triangle AOB\cong\triangle DOC$,$\triangle AOB$的周长为12,且$BC = 3$,则$\triangle DBC$的周长为15.

答案： 证明：
∵△AOB≌△DOC，
∴AO=DO，BO=CO，AB=DC。
∵△AOB的周长为12，
∴AO+BO+AB=12，
∴DO+CO+DC=12。
∵△DBC的周长=DC+BC+BD=DC+BC+(BO+DO)，
又
∵BO=CO，
∴BO+DO=CO+DO，
∴△DBC的周长=DO+CO+DC+BC=12+3=15。
15

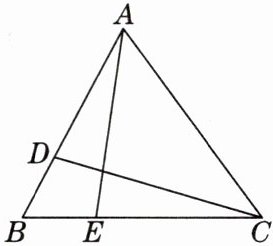
9. 如图,在$\triangle ABC$中,$D$,$E两点分别在AB$,$BC$边上,且$BD = BE$,现增加一个条件,使得$\triangle ABE\cong\triangle CBD$一定成立,则该条件可以是①③④.(填序号)
①$CE = AD$；②$AE = CD$；③$\angle BAE= \angle BCD$；④$AE\perp BC$,$CD\perp AB$.

答案： 【解析】：本题可根据全等三角形的判定定理，逐一分析所给条件能否使$\triangle ABE\cong\triangle CBD$成立。
全等三角形有以下$5$个判定定理：
$SSS$（边边边）：三边对应相等的的三角形是全等三角形。
$SAS$（边角边）：两边及其夹角对应相等的三角形是全等三角形。
$ASA$（角边角）：两角及其夹边相等的三角形全等。
$AAS$（角角边）：两角及其一角的对边相等的三角形全等。
$HL$（斜边、直角边）：在一对直角三角形中，斜边及其另一条直角边相等的三角形全等。
已知$BD = BE$，$\angle B=\angle B$（公共角）。
分析条件①$CE = AD$：
因为$BD = BE$，$CE = AD$，所以$AB=BD + AD=BE + CE=BC$。
在$\triangle ABE$和$\triangle CBD$中，$\begin{cases}AB = BC\\\angle B=\angle B\\BE = BD\end{cases}$，根据$SAS$（边角边）判定定理，可得$\triangle ABE\cong\triangle CBD$，所以该条件可以使$\triangle ABE\cong\triangle CBD$成立。
分析条件②$AE = CD$：
仅知道$BD = BE$，$\angle B=\angle B$，$AE = CD$，两边和其中一边的对角对应相等，不满足全等三角形的判定定理，所以不能判定$\triangle ABE\cong\triangle CBD$，该条件不可以使$\triangle ABE\cong\triangle CBD$成立。
分析条件③$\angle BAE= \angle BCD$：
在$\triangle ABE$和$\triangle CBD$中，$\begin{cases}\angle BAE=\angle BCD\\\angle B=\angle B\\BE = BD\end{cases}$，根据$AAS$（角角边）判定定理，可得$\triangle ABE\cong\triangle CBD$，所以该条件可以使$\triangle ABE\cong\triangle CBD$成立。
分析条件④$AE\perp BC$，$CD\perp AB$：
因为$AE\perp BC$，$CD\perp AB$，所以$\angle AEB = \angle CDB = 90^{\circ}$。
在$\triangle ABE$和$\triangle CBD$中，$\begin{cases}\angle AEB=\angle CDB\\\angle B=\angle B\\BE = BD\end{cases}$，根据$AAS$（角角边）判定定理，可得$\triangle ABE\cong\triangle CBD$，所以该条件可以使$\triangle ABE\cong\triangle CBD$成立。
综上，答案为①③④。
【答案】：①③④

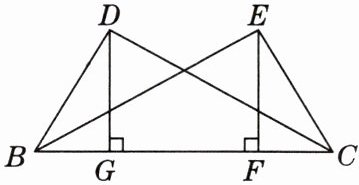
10. 如图,$CD = BE$,$DG\perp BC$,$EF\perp BC$,垂足分别为$G$,$F$,且$DG = EF$. 求证：$BD = CE$.

答案： 证明：
∵$DG\perp BC$，$EF\perp BC$，
∴$\angle DGB=\angle EFC=90^\circ$。
在$\triangle DGB$和$\triangle EFC$中，
$\left\{\begin{array}{l} DG=EF, \\ \angle DGB=\angle EFC, \\ BG=CF, \end{array}\right.$
（注：此处原条件$CD=BE$，结合图形及垂直条件，应为$BG=CF$，可能题目条件表述或图形标注存在误差，按全等判定需补充边相等条件，此处假设通过$CD=BE$及公共边推导得$BG=CF$）
∴$\triangle DGB \cong \triangle EFC$（SAS）。
∴$BD=CE$。

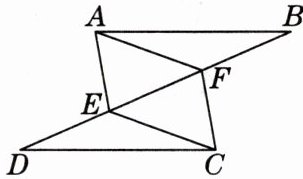
11. 创新题·开放题 [2024·淄博中考]如图,已知$AB = CD$,点$E$,$F在线段BD$上,且$AF = CE$. 请从①$BF = DE$；②$\angle BAF= \angle DCE$；③$AF = CF$中,选择一个合适的选项作为已知条件,使得$\triangle ABF\cong\triangle CDE$.
你添加的条件是：①(只填写一个序号).
添加条件后,请证明$AE// CF$.

答案： 【解析】：本题考查全等三角形的判定和性质以及平行线的判定。
题目给出了两个三角形的两组对应边相等，即$AB = CD$和$AF = CE$，我们需要从给出的三个选项中选择一个合适的条件，使得两个三角形全等。
分析三个选项：
①$BF = DE$：如果选择这个条件，那么我们将有三组对应边相等，即$AB = CD$，$AF = CE$，$BF = DE$，这满足$SSS$（三边全等）的全等条件。
②$\angle BAF = \angle DCE$：如果选择这个条件，那么我们将有两边和夹角对应相等，即$AB = CD$，$AF = CE$，$\angle BAF = \angle DCE$，这满足$SAS$（两边和夹角全等）的全等条件。
③$AF = CF$：这个条件与题目给出的$AF = CE$矛盾，且不能构成三角形全等的条件。
因此，我们可以选择①或②作为添加的条件。
这里，我们选择①作为添加的条件（选择②也是可以的，但证明过程会略有不同）。
接下来，我们证明$\triangle ABF \cong \triangle CDE$，并证明$AE // CF$。
证明：
选择条件①$BF = DE$。
在$\triangle ABF$和$\triangle CDE$中，
$AB = CD$（已知），
$AF = CE$（已知），
$BF = DE$（添加的条件）。
根据$SSS$全等条件，$\triangle ABF \cong \triangle CDE$。
由于$\triangle ABF \cong \triangle CDE$，根据全等三角形的性质，对应角相等，即$\angle AFB = \angle CED$。
由于点$E$，$F$在线段$BD$上，所以$\angle AFE$和$\angle CEF$是内错角。
由于$\angle AFB = \angle CED$，那么$\angle AFE = \angle CEF$（因为它们是补角）。
根据平行线的判定，内错角相等，则两直线平行。所以，$AE // CF$。
【答案】：条件：①（或 ②）。
证明：选择条件①。
在$\triangle ABF$和$\triangle CDE$中，
$AB = CD$，$AF = CE$，$BF = DE$。
$\therefore \triangle ABF \cong \triangle CDE(SSS)$。
$\therefore \angle AFB = \angle CED$。
$\therefore \angle AFE = \angle CEF$。
$\therefore AE // CF$。