《2025年一本九年级数学上册人教版安徽专版》

12.（2024·蚌埠期末）如图，点O是△ABC外接圆的圆心，点I是△ABC内切圆的圆心，连接OB，IA.若∠CAI=35°，则∠OBC的度数为______.

20°

答案： $20^{\circ}$

13.（教材P102习题T11变式）如图，直线AB，BC，CD分别与⊙O相切于点E，F，G，且AB//CD，OB=6 cm，OC=8 cm.求：
（1）∠BOC的度数；
（2）BE+CG的长；
（3）⊙O的半径.

答案： 【解析】：
1. 连接$OF$。
因为$AB$、$BC$、$CD$分别与$\odot O$相切于点$E$、$F$、$G$，所以$BE = BF$，$CF = CG$，$\angle OBE=\angle OBF$，$\angle OCF=\angle OCG$。
又因为$AB// CD$，所以$\angle ABC+\angle BCD = 180^{\circ}$。
则$\angle OBF+\angle OCF=\frac{1}{2}(\angle ABC+\angle BCD)=90^{\circ}$，所以$\angle BOC = 180^{\circ}-(\angle OBF+\angle OCF)=90^{\circ}$。
2. 由（1）知$\angle BOC = 90^{\circ}$，$OB = 6cm$，$OC = 8cm$，根据勾股定理$BC=\sqrt{OB^{2}+OC^{2}}=\sqrt{6^{2}+8^{2}} = 10cm$。
因为$BE = BF$，$CF = CG$，所以$BE + CG=BF + CF=BC = 10cm$。
3. 因为$BC$与$\odot O$相切于点$F$，所以$OF\perp BC$。
根据三角形面积公式$S_{\triangle BOC}=\frac{1}{2}OB\cdot OC=\frac{1}{2}BC\cdot OF$。
即$\frac{1}{2}\times6\times8=\frac{1}{2}\times10\times OF$，解得$OF = 4.8cm$，所以$\odot O$的半径为$4.8cm$。
【答案】：
（1）$90^{\circ}$；
（2）$10cm$；
（3）$4.8cm$。

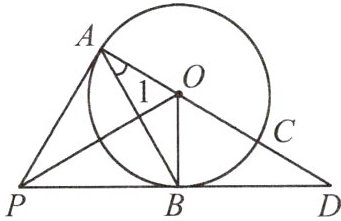
14.如图，PA，PB是⊙O的切线，切点分别为A，B，AC是⊙O的直径，AC，PB的延长线相交于点D，连接OB.
（1）若∠1=20°，求∠APB的度数；
（2）求当∠1为多少度时，OP=OD，并说明理由.

答案： 【解析】：
### $(1)$求$\angle APB$的度数
- 因为$PA$，$PB$是$\odot O$的切线，根据切线的性质可知$OA\perp PA$，$OB\perp PB$，即$\angle OAP = \angle OBP=90^{\circ}$。
- 已知$OA = OB$，$\angle 1 = 20^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle AOB=180^{\circ}-\angle 1\times2 = 180^{\circ}- 40^{\circ}=140^{\circ}$。
- 在四边形$OAPB$中，根据四边形内角和为$360^{\circ}$，则$\angle APB=360^{\circ}-\angle OAP-\angle OBP - \angle AOB$。
将$\angle OAP = 90^{\circ}$，$\angle OBP = 90^{\circ}$，$\angle AOB = 140^{\circ}$代入可得：$\angle APB=360^{\circ}-90^{\circ}-90^{\circ}-140^{\circ}=40^{\circ}$。
### $(2)$求$\angle 1$的度数使得$OP = OD$
- 若$OP = OD$，则$\angle OPD=\angle D$。
- 因为$OB\perp PD$，所以$\angle OBD = 90^{\circ}$，则$\angle BOD+\angle D = 90^{\circ}$。
- 又因为$PA$，$PB$是$\odot O$的切线，所以$\angle APO=\angle OPD=\angle D$，$\angle OAP = 90^{\circ}$，$\angle AOP=\angle BOP$。
- 由于$\angle AOP=\angle OPD+\angle D = 2\angle D$（三角形外角性质），且$\angle AOP+\angle BOP+\angle BOD = 180^{\circ}$，$\angle BOD = 90^{\circ}-\angle D$，则$2\angle AOP+\angle BOD = 180^{\circ}$，即$4\angle D+(90^{\circ}-\angle D)=180^{\circ}$。
- 化简$4\angle D + 90^{\circ}-\angle D=180^{\circ}$得$3\angle D=90^{\circ}$，解得$\angle D = 30^{\circ}$。
- 所以$\angle AOP = 60^{\circ}$，那么$\angle 1=\frac{1}{2}(180^{\circ}-\angle AOP)=\frac{1}{2}(180^{\circ}-60^{\circ}) = 30^{\circ}$。
【答案】：
$(1)$$\boldsymbol{40^{\circ}}$；$(2)$$\boldsymbol{30^{\circ}}$

方法指导 如图，在Rt△ABC中，AB=c，AC=b，BC=a，由图1可得，△ABC的内切圆半径r=(a + b - c)/2，由图2可得，r=ab/(a + b + c).

例 如图，在△ABC中，∠C=90°，AC=3，BC=4，则△ABC的内切圆⊙O的半径r=______.
变式1 如图，在△ABC中，∠C=90°，AC=12，BC=5，⊙O与△ABC的三边分别相切于点D，E，F，则AE的长为______.
变式2 如图，在△ABC中，∠C=90°，⊙I为△ABC的内切圆，点O为△ABC的外心，BC=9，AC=12，则线段OI的长为______.

答案： ### 例【解析】：本题可先根据勾股定理求出斜边$AB$的长度，再根据直角三角形内切圆半径公式$r = \frac{a + b - c}{2}$（其中$a$、$b$为直角边，$c$为斜边）来计算内切圆半径$r$。- **步骤一：求斜边$AB$的长度**在$\triangle ABC$中，$\angle C = 90^{\circ}$，$AC = 3$，$BC = 4$，根据勾股定理$AB^{2}=AC^{2}+BC^{2}$，可得：$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5$- **步骤二：计算内切圆半径$r$**将$AC = 3$，$BC = 4$，$AB = 5$代入直角三角形内切圆半径公式$r = \frac{a + b - c}{2}$（其中$a = 3$，$b = 4$，$c = 5$），可得：$r = \frac{3 + 4 - 5}{2} = \frac{2}{2} = 1$【答案】：$1$### 变式1【解析】：本题可先根据勾股定理求出斜边$AB$的长度，再根据切线长定理来计算$AE$的长度。- **步骤一：求斜边$AB$的长度**在$\triangle ABC$中，$\angle C = 90^{\circ}$，$AC = 12$，$BC = 5$，根据勾股定理$AB^{2}=AC^{2}+BC^{2}$，可得：$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{12^{2} + 5^{2}} = \sqrt{144 + 25} = \sqrt{169} = 13$- **步骤二：根据切线长定理计算$AE$的长度**因为$\odot O$与$\triangle ABC$的三边分别相切于点$D$，$E$，$F$，根据切线长定理可知：$AE = AF$，$BD = BF$，$CD = CE$。设$AE = AF = x$，则$BF = BD = AB - AF = 13 - x$，$CE = CD = AC - AE = 12 - x$。又因为$BC = BD + CD$，所以$5 = (13 - x) + (12 - x)$，去括号得$5 = 13 - x + 12 - x$，移项得$x + x = 13 + 12 - 5$，合并同类项得$2x = 20$，系数化为$1$得$x = 10$，即$AE = 10$。【答案】：$10$### 变式2【解析】：本题可先根据勾股定理求出斜边$AB$的长度，进而得到外心$O$的位置，再求出内切圆半径$r$，最后通过建立合适的坐标系来计算线段$OI$的长度。- **步骤一：求斜边$AB$的长度**在$\triangle ABC$中，$\angle C = 90^{\circ}$，$BC = 9$，$AC = 12$，根据勾股定理$AB^{2}=AC^{2}+BC^{2}$，可得：$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{12^{2} + 9^{2}} = \sqrt{144 + 81} = \sqrt{225} = 15$- **步骤二：确定外心$O$的位置**因为直角三角形的外心是斜边的中点，所以点$O$是$AB$的中点。- **步骤三：求内切圆半径$r$**根据直角三角形内切圆半径公式$r = \frac{a + b - c}{2}$（其中$a = 9$，$b = 12$，$c = 15$），可得：$r = \frac{9 + 12 - 15}{2} = \frac{6}{2} = 3$- **步骤四：建立坐标系计算线段$OI$的长度**以$C$为原点，$CA$所在直线为$x$轴，$CB$所在直线为$y$轴建立平面直角坐标系。则$A(12,0)$，$B(0,9)$，那么外心$O$的坐标为$(\frac{12 + 0}{2}, \frac{0 + 9}{2})$，即$(6, \frac{9}{2})$。因为内切圆半径$r = 3$，所以内切圆$I$的坐标为$(3,3)$。根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$（其中$(x_1, y_1)$，$(x_2, y_2)$为两点坐标），可得：$OI = \sqrt{(6 - 3)^2 + (\frac{9}{2} - 3)^2} = \sqrt{3^2 + (\frac{3}{2})^2} = \sqrt{9 + \frac{9}{4}} = \sqrt{\frac{45}{4}} = \frac{3\sqrt{5}}{2}$【答案】：$\frac{3\sqrt{5}}{2}$