第66页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1.数学来源于生活.下列生活中的各物体的运动,属于旋转的是(
A.上升的国旗
B.球场上滚动的足球
C.工作中的风力发电机叶片
D.传输带运输的东西
C
)A.上升的国旗
B.球场上滚动的足球
C.工作中的风力发电机叶片
D.传输带运输的东西
答案:
C
2.如图,把Rt△ABC的斜边AB放在直线l上,按如图所示的方式旋转,已知∠CAB=30°.
(1)第一次旋转的旋转中心是
(2)第二次旋转的旋转中心是
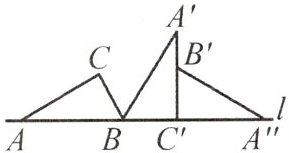
(1)第一次旋转的旋转中心是
点$B$
,旋转角度为$120^{\circ}$
;(2)第二次旋转的旋转中心是
点$C'$
,旋转角度为$90^{\circ}$
.
答案:
(1)点$B$,$120^{\circ}$;
(2)点$C'$,$90^{\circ}$。
(2)点$C'$,$90^{\circ}$。
3.(教材P59练习T2变式)时钟上的分针匀速旋转一周需要60分钟,则经过40分钟,分针旋转了
240
°.
答案:
$240$
4.(链接教材)如图,将△OAB绕顶点O逆时针旋转60°后得到△OCD.若∠AOB=25°,OA=3,则∠DOC=
25
°,∠BOD=60
°,OC=3
.
答案:
$25$,$60$,$3$。
5.如图,将直角三角尺ABC绕顶点A顺时针旋转得到△AB'C',点B'恰好落在CA的延长线上.若∠B=30°,∠C=90°,则旋转角的度数为(
A.60°
B.90°
C.120°
D.150°
C
)A.60°
B.90°
C.120°
D.150°
答案:
C
6.如图,将△ABC绕点A顺时针旋转60°后得到△AED.若AB=4,则BE的长为(
A.3
B.4
C.5
D.6
B
)A.3
B.4
C.5
D.6
答案:
B
7.(2024·芜湖镜湖区一模改编)如图,△ODC是由△OAB绕点O顺时针旋转40°后得到的图形.若点D恰好落在AB上,且∠AOC=105°,则∠C的度数是______
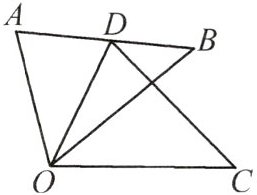
45°
.
答案:
$45^{\circ}$
8.如图,在△ABC中,∠B=45°,将△ABC绕点A逆时针旋转,得到△AB'C',使点B'在BC的延长线上.求证:BB'⊥C'B'.
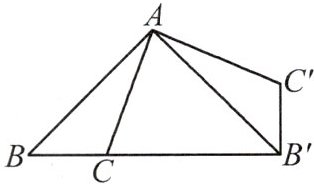

答案:
【解析】:
- 由旋转的性质可知$AB = AB'$,$\angle AB'C'=\angle B = 45^{\circ}$。
- 因为$AB = AB'$,所以$\angle B=\angle AB'B = 45^{\circ}$。
- 那么$\angle BB'C'=\angle AB'B+\angle AB'C' = 45^{\circ}+45^{\circ}=90^{\circ}$。
- 所以$BB'\perp C'B'$。
【答案】:
由旋转性质得$AB = AB'$,$\angle AB'C'=\angle B = 45^{\circ}$,因为$AB = AB'$,所以$\angle B=\angle AB'B = 45^{\circ}$,则$\angle BB'C'=\angle AB'B+\angle AB'C' = 90^{\circ}$,即$BB'\perp C'B'$。
- 由旋转的性质可知$AB = AB'$,$\angle AB'C'=\angle B = 45^{\circ}$。
- 因为$AB = AB'$,所以$\angle B=\angle AB'B = 45^{\circ}$。
- 那么$\angle BB'C'=\angle AB'B+\angle AB'C' = 45^{\circ}+45^{\circ}=90^{\circ}$。
- 所以$BB'\perp C'B'$。
【答案】:
由旋转性质得$AB = AB'$,$\angle AB'C'=\angle B = 45^{\circ}$,因为$AB = AB'$,所以$\angle B=\angle AB'B = 45^{\circ}$,则$\angle BB'C'=\angle AB'B+\angle AB'C' = 90^{\circ}$,即$BB'\perp C'B'$。
查看更多完整答案,请扫码查看


