第90页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1. 如图,四边形 $ABCD$ 内接于 $\odot O$,$AB$ 是直径,$C$ 为 $\overset{\frown}{BD}$ 的中点,延长 $AD$,$BC$ 交于点 $P$,连接 $AC$。
(1) 求证:$AB = AP$;
(2) 当 $AB = 10$,$DP = 2$ 时,求线段 $CP$ 的长。

(1) 求证:$AB = AP$;
(2) 当 $AB = 10$,$DP = 2$ 时,求线段 $CP$ 的长。

答案:
【解析】:
(1) 因为$C$为$\overset{\frown}{BD}$的中点,所以$\overset{\frown}{BC}=\overset{\frown}{CD}$,根据圆周角定理,可得$\angle BAC = \angle PAC$。
因为$AB$是直径,所以$\angle ACB=\angle ACP = 90^{\circ}$。
在$\triangle ABC$和$\triangle APC$中,$\left\{\begin{array}{l}\angle BAC=\angle PAC\\AC = AC\\\angle ACB=\angle ACP\end{array}\right.$,根据$ASA$(角边角)定理,可得$\triangle ABC\cong\triangle APC$,所以$AB = AP$。
(2) 因为$AB = AP = 10$,$DP = 2$,所以$AD=AP - DP=10 - 2 = 8$。
因为四边形$ABCD$内接于$\odot O$,所以$\angle PDC=\angle PBA$(圆内接四边形的一个外角等于它的内对角),又因为$\angle P=\angle P$,所以$\triangle PDC\sim\triangle PBA$。
根据相似三角形的性质,$\frac{CP}{AP}=\frac{DP}{BP}$,设$CP=x$,则$BC = CP=x$(由
(1)中$\triangle ABC\cong\triangle APC$),$BP=BC + CP = 2x$。
代入$\frac{CP}{AP}=\frac{DP}{BP}$,即$\frac{x}{10}=\frac{2}{2x}$,化简得$2x^{2}=20$,$x^{2}=10$,解得$x=\sqrt{10}$(负根舍去),所以$CP=\sqrt{10}$。
【答案】:
(1) 证明过程如上述解析;
(2)$\sqrt{10}$
(1) 因为$C$为$\overset{\frown}{BD}$的中点,所以$\overset{\frown}{BC}=\overset{\frown}{CD}$,根据圆周角定理,可得$\angle BAC = \angle PAC$。
因为$AB$是直径,所以$\angle ACB=\angle ACP = 90^{\circ}$。
在$\triangle ABC$和$\triangle APC$中,$\left\{\begin{array}{l}\angle BAC=\angle PAC\\AC = AC\\\angle ACB=\angle ACP\end{array}\right.$,根据$ASA$(角边角)定理,可得$\triangle ABC\cong\triangle APC$,所以$AB = AP$。
(2) 因为$AB = AP = 10$,$DP = 2$,所以$AD=AP - DP=10 - 2 = 8$。
因为四边形$ABCD$内接于$\odot O$,所以$\angle PDC=\angle PBA$(圆内接四边形的一个外角等于它的内对角),又因为$\angle P=\angle P$,所以$\triangle PDC\sim\triangle PBA$。
根据相似三角形的性质,$\frac{CP}{AP}=\frac{DP}{BP}$,设$CP=x$,则$BC = CP=x$(由
(1)中$\triangle ABC\cong\triangle APC$),$BP=BC + CP = 2x$。
代入$\frac{CP}{AP}=\frac{DP}{BP}$,即$\frac{x}{10}=\frac{2}{2x}$,化简得$2x^{2}=20$,$x^{2}=10$,解得$x=\sqrt{10}$(负根舍去),所以$CP=\sqrt{10}$。
【答案】:
(1) 证明过程如上述解析;
(2)$\sqrt{10}$
2. 如图,$AB$ 是 $\odot O$ 的直径,弦 $CD \perp AB$ 于点 $E$,$G$ 是 $\overset{\frown}{AC}$ 上的一点,$AG$ 的延长线与 $DC$ 的延长线交于点 $F$,连接 $DG$,$CG$。
(1) 若 $CD = 8$,$BE = 2$,求 $\odot O$ 的半径;
(2) 求证:$\angle FGC = \angle AGD$。

(1) 若 $CD = 8$,$BE = 2$,求 $\odot O$ 的半径;
(2) 求证:$\angle FGC = \angle AGD$。

答案:
【解析】:
### $(1)$求$\odot O$的半径
连接$OC$,因为$AB$是$\odot O$的直径,$CD\perp AB$,根据垂径定理可知$CE = DE=\frac{1}{2}CD$。
已知$CD = 8$,则$CE=\frac{1}{2}\times8 = 4$。
设$\odot O$的半径为$r$,因为$BE = 2$,所以$OE=r - 2$。
在$Rt\triangle OCE$中,根据勾股定理$OC^{2}=OE^{2}+CE^{2}$,即$r^{2}=(r - 2)^{2}+4^{2}$。
展开$(r - 2)^{2}+4^{2}$得$r^{2}=r^{2}-4r + 4+16$。
移项可得$r^{2}-r^{2}+4r=4 + 16$,即$4r=20$,解得$r = 5$。
### $(2)$证明$\angle FGC=\angle AGD$
连接$AD$,因为四边形$ADCG$是圆内接四边形,根据圆内接四边形的性质:圆内接四边形的外角等于它的内对角,所以$\angle FGC=\angle ADC$。
又因为$AB$是$\odot O$的直径,$CD\perp AB$,根据垂径定理可知$\overset{\frown}{AD}=\overset{\frown}{AC}$。
再根据圆周角定理:同弧或等弧所对的圆周角相等,所以$\angle ADC=\angle AGD$。
由$\angle FGC=\angle ADC$和$\angle ADC=\angle AGD$,可得$\angle FGC=\angle AGD$。
【答案】:
$(1)$$\boldsymbol{5}$;$(2)$证明过程如上述解析。
### $(1)$求$\odot O$的半径
连接$OC$,因为$AB$是$\odot O$的直径,$CD\perp AB$,根据垂径定理可知$CE = DE=\frac{1}{2}CD$。
已知$CD = 8$,则$CE=\frac{1}{2}\times8 = 4$。
设$\odot O$的半径为$r$,因为$BE = 2$,所以$OE=r - 2$。
在$Rt\triangle OCE$中,根据勾股定理$OC^{2}=OE^{2}+CE^{2}$,即$r^{2}=(r - 2)^{2}+4^{2}$。
展开$(r - 2)^{2}+4^{2}$得$r^{2}=r^{2}-4r + 4+16$。
移项可得$r^{2}-r^{2}+4r=4 + 16$,即$4r=20$,解得$r = 5$。
### $(2)$证明$\angle FGC=\angle AGD$
连接$AD$,因为四边形$ADCG$是圆内接四边形,根据圆内接四边形的性质:圆内接四边形的外角等于它的内对角,所以$\angle FGC=\angle ADC$。
又因为$AB$是$\odot O$的直径,$CD\perp AB$,根据垂径定理可知$\overset{\frown}{AD}=\overset{\frown}{AC}$。
再根据圆周角定理:同弧或等弧所对的圆周角相等,所以$\angle ADC=\angle AGD$。
由$\angle FGC=\angle ADC$和$\angle ADC=\angle AGD$,可得$\angle FGC=\angle AGD$。
【答案】:
$(1)$$\boldsymbol{5}$;$(2)$证明过程如上述解析。
3. 如图,$\odot O$ 的直径 $CD$ 分别与弦 $AB$,$AF$ 交于点 $E$,$H$,连接 $AD$。已知 $CF = CH$,$FB = BD$。
(1) 求证:$AB \perp CD$;
(2) 若 $AE = 4$,$OH = 1$,求 $AO$ 的长。
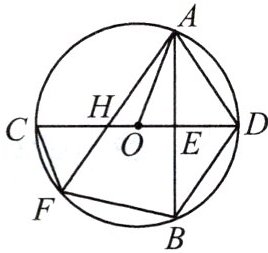
(1) 求证:$AB \perp CD$;
(2) 若 $AE = 4$,$OH = 1$,求 $AO$ 的长。

答案:
【解析】:
### $(1)$ 证明$AB\perp CD$
已知$CF = CH$,根据“等边对等角”可得$\angle COF=\angle CHO$。
因为$\angle CHO=\angle AHE$,所以$\angle COF=\angle AHE$。
又因为$FB = BD$,根据“在同圆或等圆中,相等的弧所对的圆心角相等”,可得$\angle AOD=\angle FOC$。
所以$\angle AHE=\angle AOD$。
在$\triangle AOD$中,$\angle OAD+\angle ADO+\angle AOD = 180^{\circ}$,且$OA = OD$(半径相等),所以$\angle OAD=\angle ADO$。
因为$\angle AHE+\angle HAE+\angle AEH = 180^{\circ}$,$\angle AHE=\angle AOD$,$\angle OAD=\angle ADO$,$\angle ADO=\angle HAE$(同弧所对的圆周角相等),所以$\angle AEH = 90^{\circ}$,即$AB\perp CD$。
### $(2)$ 求$AO$的长
设$AO = x$,则$OH = 1$,$AH=x + 1$。
因为$AB\perp CD$,根据垂径定理可知$AE=EB = 4$。
在$Rt\triangle AOE$中,根据勾股定理$AO^{2}=AE^{2}+OE^{2}$,即$x^{2}=4^{2}+(x - 1)^{2}$。
展开式子得$x^{2}=16+x^{2}-2x + 1$。
移项可得$2x=16 + 1$。
合并同类项得$2x=17$,解得$x=\frac{17}{2}$。
【答案】:
$(1)$ 证明过程如上述解析;$(2)$$\boldsymbol{\frac{17}{2}}$
### $(1)$ 证明$AB\perp CD$
已知$CF = CH$,根据“等边对等角”可得$\angle COF=\angle CHO$。
因为$\angle CHO=\angle AHE$,所以$\angle COF=\angle AHE$。
又因为$FB = BD$,根据“在同圆或等圆中,相等的弧所对的圆心角相等”,可得$\angle AOD=\angle FOC$。
所以$\angle AHE=\angle AOD$。
在$\triangle AOD$中,$\angle OAD+\angle ADO+\angle AOD = 180^{\circ}$,且$OA = OD$(半径相等),所以$\angle OAD=\angle ADO$。
因为$\angle AHE+\angle HAE+\angle AEH = 180^{\circ}$,$\angle AHE=\angle AOD$,$\angle OAD=\angle ADO$,$\angle ADO=\angle HAE$(同弧所对的圆周角相等),所以$\angle AEH = 90^{\circ}$,即$AB\perp CD$。
### $(2)$ 求$AO$的长
设$AO = x$,则$OH = 1$,$AH=x + 1$。
因为$AB\perp CD$,根据垂径定理可知$AE=EB = 4$。
在$Rt\triangle AOE$中,根据勾股定理$AO^{2}=AE^{2}+OE^{2}$,即$x^{2}=4^{2}+(x - 1)^{2}$。
展开式子得$x^{2}=16+x^{2}-2x + 1$。
移项可得$2x=16 + 1$。
合并同类项得$2x=17$,解得$x=\frac{17}{2}$。
【答案】:
$(1)$ 证明过程如上述解析;$(2)$$\boldsymbol{\frac{17}{2}}$
4. 如图,以 $AB$ 为直径的 $\odot O$ 经过 $\triangle ABC$ 的顶点 $C$,$AE$,$BE$ 分别平分 $\angle BAC$ 和 $\angle ABC$,$AE$ 的延长线交 $\odot O$ 于点 $D$,连接 $BD$。
(1) 判断 $\triangle BDE$ 的形状,并说明理由;
(2) 若 $AB = 10$,$BE = 2\sqrt{10}$,求 $BC$ 的长。
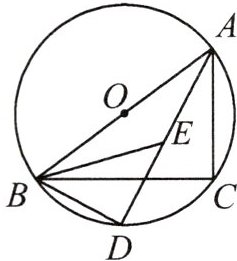
(1) 判断 $\triangle BDE$ 的形状,并说明理由;
(2) 若 $AB = 10$,$BE = 2\sqrt{10}$,求 $BC$ 的长。

答案:
【解析】:
### $(1)$ 判断$\triangle BDE$的形状
- 因为$AE$平分$\angle BAC$,$BE$平分$\angle ABC$,所以$\angle BAE=\angle CAD=\angle CBD$,$\angle ABE = \angle EBC$。
- 由于$\angle BED=\angle BAE+\angle ABE$,$\angle DBE=\angle DBC+\angle CBE$。
- 又因为$\angle BAE=\angle CBD$,$\angle ABE = \angle EBC$,所以$\angle BED=\angle DBE$。
- 因为$AB$是直径,所以$\angle ADB = 90^{\circ}$(直径所对的圆周角是直角)。
- 在$\triangle BDE$中,$\angle ADB = 90^{\circ}$且$\angle BED=\angle DBE$,所以$\triangle BDE$是等腰直角三角形。
### $(2)$ 求$BC$的长
- 连接$OD$交$BC$于点$F$。
- 因为$\angle BAD=\angle CAD$,所以$\overset{\frown}{BD}=\overset{\frown}{CD}$(相等的圆周角所对的弧相等)。
- 根据垂径定理,$OD\perp BC$,$BC = 2BF$。
- 因为$AB$是直径,$AB = 10$,所以$OB = OD=\frac{1}{2}AB = 5$。
- 由$(1)$知$\triangle BDE$是等腰直角三角形,$BE = 2\sqrt{10}$,所以$BD=\frac{BE}{\sqrt{2}}=\frac{2\sqrt{10}}{\sqrt{2}} = 2\sqrt{5}$。
- 设$OF=x$,则$DF = 5 - x$。
- 在$Rt\triangle BOF$中,$BF^{2}=OB^{2}-OF^{2}=25 - x^{2}$;在$Rt\triangle BDF$中,$BF^{2}=BD^{2}-DF^{2}=20-(5 - x)^{2}$。
- 所以$25 - x^{2}=20-(5 - x)^{2}$,展开$20-(5 - x)^{2}$得$20-(25 - 10x+x^{2})=- 5+10x - x^{2}$。
- 则$25 - x^{2}=-5 + 10x - x^{2}$,移项可得$10x=30$,解得$x = 3$。
- 把$x = 3$代入$BF^{2}=25 - x^{2}$,得$BF^{2}=25 - 9 = 16$,所以$BF = 4$。
- 那么$BC = 2BF=8$。
【答案】:
$(1)$ $\triangle BDE$是等腰直角三角形,理由见上述解析;$(2)$ $8$
### $(1)$ 判断$\triangle BDE$的形状
- 因为$AE$平分$\angle BAC$,$BE$平分$\angle ABC$,所以$\angle BAE=\angle CAD=\angle CBD$,$\angle ABE = \angle EBC$。
- 由于$\angle BED=\angle BAE+\angle ABE$,$\angle DBE=\angle DBC+\angle CBE$。
- 又因为$\angle BAE=\angle CBD$,$\angle ABE = \angle EBC$,所以$\angle BED=\angle DBE$。
- 因为$AB$是直径,所以$\angle ADB = 90^{\circ}$(直径所对的圆周角是直角)。
- 在$\triangle BDE$中,$\angle ADB = 90^{\circ}$且$\angle BED=\angle DBE$,所以$\triangle BDE$是等腰直角三角形。
### $(2)$ 求$BC$的长
- 连接$OD$交$BC$于点$F$。
- 因为$\angle BAD=\angle CAD$,所以$\overset{\frown}{BD}=\overset{\frown}{CD}$(相等的圆周角所对的弧相等)。
- 根据垂径定理,$OD\perp BC$,$BC = 2BF$。
- 因为$AB$是直径,$AB = 10$,所以$OB = OD=\frac{1}{2}AB = 5$。
- 由$(1)$知$\triangle BDE$是等腰直角三角形,$BE = 2\sqrt{10}$,所以$BD=\frac{BE}{\sqrt{2}}=\frac{2\sqrt{10}}{\sqrt{2}} = 2\sqrt{5}$。
- 设$OF=x$,则$DF = 5 - x$。
- 在$Rt\triangle BOF$中,$BF^{2}=OB^{2}-OF^{2}=25 - x^{2}$;在$Rt\triangle BDF$中,$BF^{2}=BD^{2}-DF^{2}=20-(5 - x)^{2}$。
- 所以$25 - x^{2}=20-(5 - x)^{2}$,展开$20-(5 - x)^{2}$得$20-(25 - 10x+x^{2})=- 5+10x - x^{2}$。
- 则$25 - x^{2}=-5 + 10x - x^{2}$,移项可得$10x=30$,解得$x = 3$。
- 把$x = 3$代入$BF^{2}=25 - x^{2}$,得$BF^{2}=25 - 9 = 16$,所以$BF = 4$。
- 那么$BC = 2BF=8$。
【答案】:
$(1)$ $\triangle BDE$是等腰直角三角形,理由见上述解析;$(2)$ $8$
查看更多完整答案,请扫码查看


