第49页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
8.二次函数$y=ax^{2}+bx+c$的部分图象如图所示,由图象可知不等式$ax^{2}+bx+c≥0$的解集是
$-1\leq x\leq5$
.
答案:
$-1\leq x\leq5$
9.抛物线$y=-x^{2}+4x-4$与坐标轴的交点的个数为(
A.0
B.1
C.2
D.3
C
)A.0
B.1
C.2
D.3
答案:
C
10.若抛物线$y=kx^{2}-3x-2$与x轴有两个不同的交点,则k的取值范围是
$k>-\frac{9}{8}$且$k\neq0$
.
答案:
$k>-\frac{9}{8}$且$k\neq0$
11.在同一平面直角坐标系中,抛物线$y_{1}=-x^{2}+4x$和直线$y_{2}=2x$如图所示,那么$y_{1}>y_{2}$的解集是(
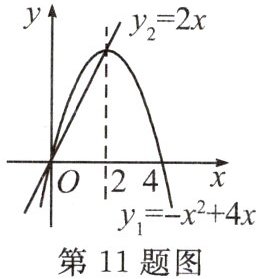
A.$x<0$
B.$0<x<2$
C.$x>2$
D.$x<0$或$x>2$
B
)
A.$x<0$
B.$0<x<2$
C.$x>2$
D.$x<0$或$x>2$
答案:
B
12.在平面直角坐标系中,抛物线$y=ax^{2}+bx+c$与直线$y=mx+n$如图所示,那么方程$ax^{2}+(b-m)x+(c-n)=0$的解为(
A.$x_{1}=0,x_{2}=3$
B.$x_{1}=-3,x_{2}=3$
C.$x_{1}=-1,x_{2}=3$
D.$x_{1}=-3,x_{2}=0$
C
)A.$x_{1}=0,x_{2}=3$
B.$x_{1}=-3,x_{2}=3$
C.$x_{1}=-1,x_{2}=3$
D.$x_{1}=-3,x_{2}=0$
答案:
C
13.已知抛物线$y=(x-m)^{2}+n$与x轴交于点$(1,0),(4,0)$,则关于x的一元二次方程$(x-m-3)^{2}+n=0$的解是
$x_1 = 4$,$x_2 = 7$
.
答案:
$x_1 = 4$,$x_2 = 7$
14.已知二次函数$y=ax^{2}+bx+c(a≠0)$的自变量x与函数值y的部分对应值如下表:
|x|…|-3|-2|0|1|3|5|…|
|----|----|----|----|----|----|----|----|----|
|y|…|7|0|-8|-9|-5|7|…|
同学们经过讨论得出了下列结论:①二次函数图象的开口向上;②二次函数图象的对称轴为$x=2$;③当$-2<x<4$时,$y<0$;④$x=3$是关于x的方程$ax^{2}+bx+c+5=0$的一个根.其中正确的结论是
|x|…|-3|-2|0|1|3|5|…|
|----|----|----|----|----|----|----|----|----|
|y|…|7|0|-8|-9|-5|7|…|
同学们经过讨论得出了下列结论:①二次函数图象的开口向上;②二次函数图象的对称轴为$x=2$;③当$-2<x<4$时,$y<0$;④$x=3$是关于x的方程$ax^{2}+bx+c+5=0$的一个根.其中正确的结论是
①③④
.(填序号)
答案:
①③④
15.【一题多问】某兴趣小组对函数$y=-x^{2}+2|x|$的图象和性质进行了探究,探究过程如下,请补充完整.自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
|x|…|-3|$-\frac{5}{2}$|-2|-1|0|1|2|$\frac{5}{2}$|3|…|
|----|----|----|----|----|----|----|----|----|----|----|----|
|y|…|-3|$-\frac{5}{4}$|0|1|0|1|0|$-\frac{5}{4}$|-3|…|
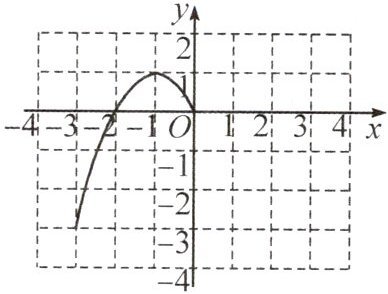
(1)根据上表数据,在如图所示的平面直角坐标系中画出了函数图象的一部分,请画出该函数图象的另一部分.
(2)观察函数图象,当y随x的增大而减小时,x的取值范围是
(3)进一步探究函数图象发现:
①函数图象与x轴有
②方程$-x^{2}+2|x|=-1$有
③若关于x的方程$-x^{2}+2|x|=n$有4个实数根,则n的取值范围是
温馨提示:学习至此,建议使用本书第141~142页周周清小卷4(22.1.4~22.2)
|x|…|-3|$-\frac{5}{2}$|-2|-1|0|1|2|$\frac{5}{2}$|3|…|
|----|----|----|----|----|----|----|----|----|----|----|----|
|y|…|-3|$-\frac{5}{4}$|0|1|0|1|0|$-\frac{5}{4}$|-3|…|
(1)根据上表数据,在如图所示的平面直角坐标系中画出了函数图象的一部分,请画出该函数图象的另一部分.
(2)观察函数图象,当y随x的增大而减小时,x的取值范围是
$-1\lt x\lt0$或$x\gt1$
.(3)进一步探究函数图象发现:
①函数图象与x轴有
3
个交点,所以对应方程$-x^{2}+2|x|=0$有3
个实数根;②方程$-x^{2}+2|x|=-1$有
2
个实数根;③若关于x的方程$-x^{2}+2|x|=n$有4个实数根,则n的取值范围是
$0\lt n\lt1$
.温馨提示:学习至此,建议使用本书第141~142页周周清小卷4(22.1.4~22.2)

答案:
【解析】:
(1)根据函数$y = -x^{2}+2|x|$是偶函数,图象关于$y$轴对称,可画出另一部分图象。
(2)观察函数图象,当$y$随$x$的增大而减小时,$x$的取值范围是$-1\lt x\lt0$或$x\gt1$。
(3)①函数图象与$x$轴有$3$个交点,所以对应方程$-x^{2}+2|x| = 0$有$3$个实数根;
②方程$-x^{2}+2|x|=-1$,即$y=-x^{2}+2|x|$与$y = -1$的交点个数,通过图象可知有$2$个实数根;
③若关于$x$的方程$-x^{2}+2|x|=n$有$4$个实数根,即$y=-x^{2}+2|x|$与$y = n$有$4$个交点,通过图象可知$n$的取值范围是$0\lt n\lt1$。
【答案】:
(2)$-1\lt x\lt0$或$x\gt1$
(3)①$3$,$3$;②$2$;③$0\lt n\lt1$
(1)根据函数$y = -x^{2}+2|x|$是偶函数,图象关于$y$轴对称,可画出另一部分图象。
(2)观察函数图象,当$y$随$x$的增大而减小时,$x$的取值范围是$-1\lt x\lt0$或$x\gt1$。
(3)①函数图象与$x$轴有$3$个交点,所以对应方程$-x^{2}+2|x| = 0$有$3$个实数根;
②方程$-x^{2}+2|x|=-1$,即$y=-x^{2}+2|x|$与$y = -1$的交点个数,通过图象可知有$2$个实数根;
③若关于$x$的方程$-x^{2}+2|x|=n$有$4$个实数根,即$y=-x^{2}+2|x|$与$y = n$有$4$个交点,通过图象可知$n$的取值范围是$0\lt n\lt1$。
【答案】:
(2)$-1\lt x\lt0$或$x\gt1$
(3)①$3$,$3$;②$2$;③$0\lt n\lt1$
查看更多完整答案,请扫码查看


