《2025年一本九年级数学上册人教版安徽专版》

1. 直线$y = ax + b$与抛物线$y = ax^{2}+bx + b$在同一平面直角坐标系中的大致图象正确的是（B）

答案： B

2. 二次函数$y = ax^{2}+bx + 1$与一次函数$y = 2ax + b$在同一平面直角坐标系中的图象可能是（B）

答案： B

3. (2024·青岛)二次函数$y = ax^{2}+bx + c$的图象如图所示，对称轴是$x = - 1$，则过点$M(c,2a - b)$和点$N(b^{2}-4ac,a - b + c)$的直线一定不经过（A）

A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： A

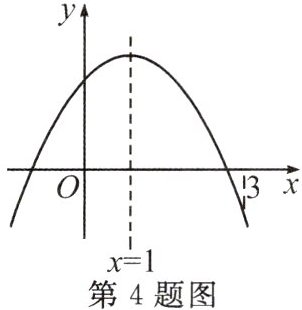
4. 二次函数$y = ax^{2}+bx + c(a\neq0)$的图象如图所示，有下列结论：①$abc＞0$；②$2a + b = 0$；③若$m$为任意实数，则$a + b＞am^{2}+bm$；④$a - b + c＞0$；⑤若$ax_{1}^{2}+bx_{1}=ax_{2}^{2}+bx_{2}$，且$x_{1}\neq x_{2}$，则$x_{1}+x_{2}=2$。其中正确的结论为（D）

A. ①②③④⑤
B. ②
C. ②③⑤
D. ②⑤

答案： D

5. 若某二次函数在$x = - 4$时取得最大值，最大值为$\sqrt{3}$，其图象在$x$轴上截得的线段$AB$（点$A$在点$B$的右边）的长为$6$，求该二次函数的解析式。

答案： 【解析】：
因为二次函数在$x = - 4$时取得最大值$\sqrt{3}$，所以可设二次函数的顶点式为$y=a(x + 4)^{2}+\sqrt{3}(a\lt0)$。
设二次函数图象与$x$轴的交点$A(x_{1},0)$，$B(x_{2},0)$（$x_{1}\gt x_{2}$），已知图象在$x$轴上截得的线段$AB$的长为$6$，则$x_{1}-x_{2}=6$。
令$y = 0$，则$a(x + 4)^{2}+\sqrt{3}=0$，展开可得$a(x^{2}+8x + 16)+\sqrt{3}=0$，即$ax^{2}+8ax+16a+\sqrt{3}=0$。
对于一元二次方程$mx^{2}+nx + p = 0(m\neq0)$，若其两根为$x_{3}$，$x_{4}$，根据韦达定理有$x_{3}+x_{4}=-\frac{n}{m}$，$x_{3}x_{4}=\frac{p}{m}$。
在方程$ax^{2}+8ax+16a+\sqrt{3}=0$中，$m = a$，$n = 8a$，$p = 16a+\sqrt{3}$，所以$x_{1}+x_{2}=-\frac{8a}{a}=-8$，$x_{1}x_{2}=\frac{16a+\sqrt{3}}{a}$。
又因为$(x_{1}-x_{2})^{2}=(x_{1}+x_{2})^{2}-4x_{1}x_{2}$，把$x_{1}-x_{2}=6$，$x_{1}+x_{2}=-8$，$x_{1}x_{2}=\frac{16a+\sqrt{3}}{a}$代入可得：
$6^{2}=(-8)^{2}-4\times\frac{16a+\sqrt{3}}{a}$
$36 = 64-\frac{64a + 4\sqrt{3}}{a}$
$\frac{64a + 4\sqrt{3}}{a}=64 - 36$
$\frac{64a + 4\sqrt{3}}{a}=28$
$64a+4\sqrt{3}=28a$
$64a-28a=-4\sqrt{3}$
$36a=-4\sqrt{3}$
$a=-\frac{\sqrt{3}}{9}$。
所以二次函数的解析式为$y =-\frac{\sqrt{3}}{9}(x + 4)^{2}+\sqrt{3}$。
【答案】：$y =-\frac{\sqrt{3}}{9}(x + 4)^{2}+\sqrt{3}$

6. 已知抛物线$y = ax^{2}+bx + 1(a\neq0)$经过点$(1,-2)$，$(-2,19)$。
(1) 求$a$，$b$的值；
(2) 若$A(m,p)$和$B(n,p)$是抛物线上不同的两点，且$m - n=\frac{1}{2}$，求$m$，$n$的值。

答案： 【解析】：
(1) 因为抛物线$y = ax^{2}+bx + 1(a\neq0)$经过点$(1,-2)$，$(-2,19)$，将点代入抛物线方程可得方程组：
$\begin{cases}a\times1^{2}+b\times1 + 1=-2\\a\times(-2)^{2}+b\times(-2)+1 = 19\end{cases}$
即$\begin{cases}a + b+1=-2\\4a-2b + 1=19\end{cases}$
对第一个方程进行化简：$a + b=-3$，变形为$b=-3 - a$。
将$b=-3 - a$代入第二个方程$4a-2b + 1=19$中：
$4a-2(-3 - a)+1 = 19$
$4a + 6+2a+1 = 19$
$6a+7 = 19$
$6a=19 - 7$
$6a = 12$
解得$a = 2$。
把$a = 2$代入$b=-3 - a$，得$b=-3 - 2=-5$。
(2) 由
(1)可知抛物线的解析式为$y = 2x^{2}-5x + 1$。
因为$A(m,p)$和$B(n,p)$是抛物线上不同的两点，且纵坐标相同，所以$A$、$B$关于抛物线的对称轴对称。
对于二次函数$y=Ax^{2}+Bx + C(A\neq0)$，其对称轴公式为$x =-\frac{B}{2A}$，在$y = 2x^{2}-5x + 1$中，$A = 2$，$B=-5$，则对称轴为$x=\frac{5}{4}$。
所以$\frac{m + n}{2}=\frac{5}{4}$，即$m + n=\frac{5}{2}$。
又已知$m - n=\frac{1}{2}$，联立方程组$\begin{cases}m + n=\frac{5}{2}\\m - n=\frac{1}{2}\end{cases}$
将两式相加可得：$(m + n)+(m - n)=\frac{5}{2}+\frac{1}{2}$
$2m=3$，解得$m=\frac{3}{2}$。
把$m=\frac{3}{2}$代入$m + n=\frac{5}{2}$，得$\frac{3}{2}+n=\frac{5}{2}$，解得$n = 1$。
【答案】：
(1)$a = 2$，$b=-5$；
(2)$m=\frac{3}{2}$，$n = 1$