《2025年一本九年级数学上册人教版安徽专版》

7. (教材P52习题T7变式)如图，在正方形ABCD中，点E，F，G，H分别从点A，B，C，D同时出发，均以1cm/s的速度分别向点B，C，D，A匀速运动，当点E到达点B时，四个点同时停止运动.在运动过程中，若AB=6cm，当运动时间为3s时，四边形EFGH的面积最小，最小面积为18cm²；若AB=acm，当运动时间为$\frac{a}{2}$s时，四边形EFGH的面积最小，最小面积为$\frac{a^{2}}{2}$cm².

答案： $3$，$18$，$\frac{a}{2}$，$\frac{a^{2}}{2}$

8. 工匠师傅准备从六边形的铁皮ABCDEF中，裁出一块如图所示的矩形铁皮制作工件.经测量，AB//DE，AB与DE之间的距离为2m，AB=3m，AF=BC=1m，∠A=∠B=90°，∠C=∠F=135°.MH，HG，GN是工匠师傅画出的裁剪虚线.当MH的长度为多少时，矩形铁皮MNGH的面积最大?最大面积是多少?

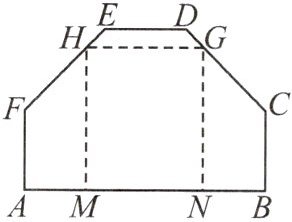
答案： 【解析】：
过点$F$作$FP\perp AB$于点$P$，过点$C$作$CQ\perp AB$于点$Q$。
因为$\angle A = \angle B=90^{\circ}$，$\angle AFP=\angle BCQ = 45^{\circ}$，$AF = BC = 1m$，所以$AP = BQ=\frac{\sqrt{2}}{2}m$。
设$MH = xm$，则$AM=(1 - x)m$（$0\lt x\lt1$）。
$MN=AB-(AM + BN)=3-(1 - x)-(1 - x)=1 + 2x$。
根据矩形面积公式$S = MH\times MN$，可得$S=x(1 + 2x)=2x^{2}+x$。
对于二次函数$y = ax^{2}+bx + c$（$a\neq0$），这里$a = 2$，$b = 1$，$c = 0$，其对称轴为$x=-\frac{b}{2a}=-\frac{1}{2\times2}=-\frac{1}{4}$，因为$a = 2\gt0$，函数图象开口向上，在对称轴右侧$y$随$x$的增大而增大，又因为$0\lt x\lt1$，所以当$x=\frac{1}{4}$时，$S$有最大值。
$S_{max}=2\times(\frac{1}{4})^{2}+\frac{1}{4}=2\times\frac{1}{16}+\frac{1}{4}=\frac{1}{8}+\frac{2}{8}=\frac{3}{8}$。
【答案】：当$MH$的长度为$\frac{1}{4}m$时，矩形铁皮$MNGH$的面积最大，最大面积是$\frac{3}{8}m^{2}$。

9. 某花圃基地计划将如图所示的一块长40m、宽20m的矩形空地划分为五块小矩形区域.其中一块正方形空地为育苗区，另一块空地为活动区，其余空地为种植区，分别种植A，B，C三种花卉.活动区一边与育苗区等宽，另一边长为10m.A，B，C三种花卉每平方米的产值分别为200元、300元、400元.
(1)设育苗区的边长为xm，请用含x的代数式表示下列各量：花卉A的种植面积为$x^{2}-60x + 800$m²，花卉B的种植面积为$-x^{2}+20x$m²，花卉C的种植面积为$-x^{2}+30x - 200$m².
(2)当育苗区的边长为多少时，A，B两种花卉的产值相等?
16m
(3)若A，B两种花卉的种植面积之和不超过560m²，求A，B，C三种花卉的总产值的最大值.
90000元

答案： 【解析】：
### $(1)$ 求花卉$A$、$B$、$C$的种植面积
- 花卉$A$：已知矩形空地长$40m$、宽$20m$，育苗区边长为$xm$，活动区长为$10m$，则花卉$A$种植区的长为$(40 - x)m$，宽为$(20 - x)m$，根据矩形面积公式$S = 长\times宽$，可得花卉$A$的种植面积$S_{A}=(40 - x)(20 - x)=800-40x - 20x+x^{2}=x^{2}-60x + 800$ $m^{2}$。
- 花卉$B$：花卉$B$种植区的长为$(20 - x)m$，宽为$x m$，根据矩形面积公式，可得花卉$B$的种植面积$S_{B}=x(20 - x)=-x^{2}+20x$ $m^{2}$。
- 花卉$C$：花卉$C$种植区的长为$(20 - x)m$，宽为$(x - 10)m$，根据矩形面积公式，可得花卉$C$的种植面积$S_{C}=(x - 10)(20 - x)=-x^{2}+30x - 200$ $m^{2}$。
### $(2)$ 求当$A$，$B$两种花卉的产值相等时育苗区的边长
已知$A$，$B$两种花卉每平方米的产值分别为$200$元、$300$元，当$A$，$B$两种花卉的产值相等时，可列方程：
$200(x^{2}-60x + 800)=300(-x^{2}+20x)$
化简得：$2(x^{2}-60x + 800)=3(-x^{2}+20x)$
$2x^{2}-120x + 1600=-3x^{2}+60x$
移项得：$2x^{2}+3x^{2}-120x - 60x + 1600 = 0$
$5x^{2}-180x + 1600 = 0$
两边同时除以$5$得：$x^{2}-36x + 320 = 0$
因式分解得：$(x - 16)(x - 20)=0$
解得$x_{1}=16$，$x_{2}=20$（因为$x\lt20$，所以舍去$x = 20$）。
### $(3)$ 求$A$，$B$，$C$三种花卉的总产值的最大值
- 首先求$x$的取值范围：
已知$A$，$B$两种花卉的种植面积之和不超过$560m^{2}$，即$S_{A}+S_{B}=(x^{2}-60x + 800)+(-x^{2}+20x)\leq560$
$x^{2}-60x + 800 - x^{2}+20x\leq560$
$-40x\leq560 - 800$
$-40x\leq-240$
解得$x\geq6$。
又因为$\begin{cases}x\gt10\\20 - x\gt0\end{cases}$，即$10\lt x\lt20$，所以$10\lt x\lt20$。
- 然后求总产值$W$的表达式：
$W = 200(x^{2}-60x + 800)+300(-x^{2}+20x)+400(-x^{2}+30x - 200)$
$=200x^{2}-12000x + 160000-300x^{2}+6000x - 400x^{2}+12000x - 80000$
$=(200x^{2}-300x^{2}-400x^{2})+(-12000x + 6000x + 12000x)+(160000 - 80000)$
$=-500x^{2}+6000x + 80000$
$=-500(x^{2}-12x)+80000$
$=-500(x^{2}-12x + 36 - 36)+80000$
$=-500((x - 6)^{2}-36)+80000$
$=-500(x - 6)^{2}+18000 + 80000$
$=-500(x - 6)^{2}+98000$。
因为$-500\lt0$，所以该二次函数图象开口向下，在对称轴$x = 6$右侧$W$随$x$的增大而减小，又因为$10\lt x\lt20$，所以当$x = 10$时，$W$有最大值。
把$x = 10$代入$W=-500(x - 6)^{2}+98000$得：
$W=-500\times(10 - 6)^{2}+98000=-500\times16 + 98000=-8000 + 98000 = 90000$（元）。
【答案】：
$(1)$$\boldsymbol{x^{2}-60x + 800}$；$\boldsymbol{-x^{2}+20x}$；$\boldsymbol{-x^{2}+30x - 200}$。
$(2)$$\boldsymbol{16m}$。
$(3)$$\boldsymbol{90000}$元。