《2025年一本九年级数学上册人教版安徽专版》

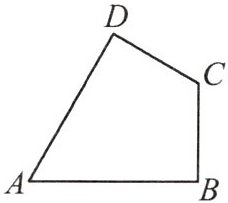
例 6 如图，在四边形 ABCD 中，AB = AD = 6，∠BAD = 60°，∠BCD = 120°。四边形 ABCD 的周长是否存在最大值？若存在，请求出最大值；若不存在，请说明理由。

答案： 【解析】：连接$BD$。
因为$AB = AD = 6$，$\angle BAD = 60^{\circ}$，所以$\triangle ABD$是等边三角形，则$BD = 6$。
因为$\angle BCD = 120^{\circ}$，根据圆内接四边形对角互补可知，$A$、$B$、$C$、$D$四点共圆，且$\triangle ABD$的外接圆半径$R = \frac{BD}{\sqrt{3}} = 2\sqrt{3}$。
由余弦定理$BD^{2}=BC^{2}+CD^{2}-2BC\cdot CD\cdot\cos\angle BCD$，即$36 = BC^{2}+CD^{2}+BC\cdot CD=(BC + CD)^{2}-BC\cdot CD$。
根据基本不等式$BC\cdot CD\leqslant(\frac{BC + CD}{2})^{2}$（当且仅当$BC = CD$时取等号）。
设$BC + CD = x$，则$36=x^{2}-BC\cdot CD\geqslant x^{2}-\frac{x^{2}}{4}=\frac{3x^{2}}{4}$，解得$x\leqslant 4\sqrt{3}$。
四边形$ABCD$的周长$L = AB + AD + BC + CD=12 + BC + CD$。
【答案】：存在，最大值为$12 + 4\sqrt{3}$。

1. 如图，在 Rt△ABC 中，AB⊥BC，AB = 6，BC = 4，P 是△ABC 内部的一个动点，且满足∠PAB = ∠PBC，则线段 CP 长的最小值为（B）
A. $\frac{3}{2}$
B. 2
C. $\frac{8\sqrt{13}}{13}$
D. $\frac{12\sqrt{13}}{13}$

答案： B

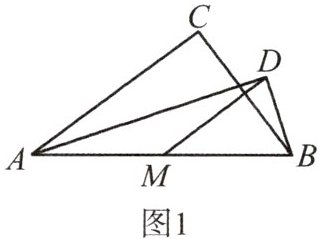
2. (2023·安徽节选)如图，在 Rt△ABC 中，M 是斜边 AB 的中点，将线段 MA 绕点 M 旋转至 MD 的位置，点 D 不在直线 AB 上，连接 AD，BD。
(1) 如图 1，求∠ADB 的度数。
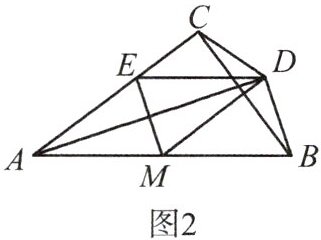
(2) 如图 2，已知 E 是边 AC 上一点，且满足 ME⊥AD，DE//AB，连接 CD。求证：BD = CD。

答案： 【解析】：
### $(1)$ 求$\angle ADB$的度数
已知$M$是$Rt\triangle ABC$斜边$AB$的中点，则$MA = MB$。
因为线段$MA$绕点$M$旋转至$MD$的位置，所以$MA = MD$，那么$MA = MB = MD$。
在$\triangle ADB$中，$MA = MD$，所以$\angle MAD=\angle MDA$；$MB = MD$，所以$\angle MBD=\angle MDB$。
因为$\angle MAD+\angle MDA+\angle MBD+\angle MDB = 180^{\circ}$，所以$2(\angle MDA+\angle MDB)=180^{\circ}$，即$\angle ADB=\angle MDA+\angle MDB = 90^{\circ}$。
### $(2)$ 证明$BD = CD$
因为$MA = MD$，$ME\perp AD$，根据等腰三角形三线合一的性质，可得$AE = DE$，所以$\angle EAD=\angle EDA$。
又因为$DE// AB$，所以$\angle EDA=\angle DAB$，则$\angle EAD=\angle DAB$。
因为$M$是$AB$中点，$\angle ACB = 90^{\circ}$，所以$CM = AM = BM$，又$MA = MD$，所以$CM = MD$，$\angle MAC=\angle MCA$。
因为$\angle EAD=\angle DAB$，$\angle MAC=\angle MCA$，所以$\angle MCA=\angle DAB$。
因为$\angle ADB = 90^{\circ}$，$\angle ACB = 90^{\circ}$，所以$A$、$C$、$B$、$D$四点共圆（四边形对角互补，四点共圆）。
由于$\angle EAD=\angle DAB$，根据同圆或等圆中，相等的圆周角所对的弦相等，所以$\overset{\frown}{CD}=\overset{\frown}{BD}$。
再根据同圆或等圆中，等弧所对的弦相等，可得$BD = CD$。
【答案】：
$(1)$$\boldsymbol{90^{\circ}}$；$(2)$证明过程如上述解析，证得$\boldsymbol{BD = CD}$。

3. 如图，四边形 ABCD 的边 CD 和 BC 的长是关于 x 的方程 $\frac{1}{2}x^2 - (m + 2)x + (2m^2 - m + \frac{7}{2}) = 0$ 的两个实数根，∠DAB = ∠DCB = 90°，AD = 2，求 AC 的长。

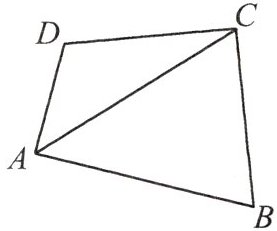
答案： $ A C = \sqrt { 2 } + \sqrt { 7 } $

4. 如图，在正方形 ABCD 中，点 E，F 分别在边 DC，CB 上移动，且 DE = CF，AE，DF 交于点 P，连接 CP，EF，当线段 CP 的长度最小时，求证：∠BAP = ∠FEC。

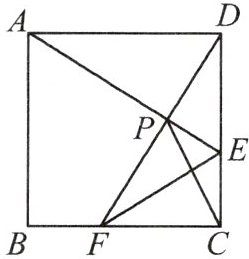
答案： 【解析】：
- 首先证明$\triangle ADE\cong\triangle DCF$：
因为四边形$ABCD$是正方形，所以$AD = DC$，$\angle ADE=\angle DCF = 90^{\circ}$。
又因为$DE = CF$，根据$SAS$（边角边）定理可得$\triangle ADE\cong\triangle DCF$。
所以$\angle DAE=\angle CDF$。
因为$\angle DAE+\angle AED = 90^{\circ}$，所以$\angle CDF+\angle AED = 90^{\circ}$，则$\angle DPE = 90^{\circ}$，即$AE\perp DF$。
点$P$的轨迹是以$AD$为直径的一段弧（设$AD$中点为$O$）。
- 然后求$CP$最小时的情况：
根据两点之间线段最短，当$O$，$P$，$C$三点共线时，$CP$最短。
此时$AP$平分$\angle DAB$（因为$OA = OP$，$\angle OAP=\angle OPA$，$AB// OP$，所以$\angle OAP=\angle PAB$），所以$\angle BAP = 45^{\circ}$。
- 接着证明$\angle FEC = 45^{\circ}$：
设正方形边长为$a$，$DE = CF=x$，则$CE=a - x$，$CF=x$。
在$Rt\triangle ECF$中，$\tan\angle FEC=\frac{CF}{CE}$，当$CP$最小时，$x=\frac{a}{2}$（可通过相似或坐标法等方法推导，这里简单说明：因为$O$为$AD$中点，$AD = a$，$OP=\frac{a}{2}$，通过全等和相似关系可得$DE=\frac{a}{2}$）。
此时$CE = CF=\frac{a}{2}$，在$Rt\triangle ECF$中，$\angle FEC = 45^{\circ}$。
【答案】：
因为四边形$ABCD$是正方形，所以$AD = DC$，$\angle ADE=\angle DCF = 90^{\circ}$，又$DE = CF$，所以$\triangle ADE\cong\triangle DCF(SAS)$，$\angle DAE=\angle CDF$，$\angle AED+\angle DAE = 90^{\circ}$，则$\angle AED+\angle CDF = 90^{\circ}$，$\angle DPE = 90^{\circ}$，点$P$在以$AD$为直径的圆上。当$CP$最小时，$AP$平分$\angle DAB$，$\angle BAP = 45^{\circ}$。设正方形边长为$a$，当$CP$最小时$DE = CF=\frac{a}{2}$，在$Rt\triangle ECF$中，$CE = CF=\frac{a}{2}$，$\angle FEC = 45^{\circ}$，所以$\angle BAP=\angle FEC$。