《2025年一本九年级数学上册人教版安徽专版》

9.(2025·阜阳太和期中)下图是一种用于液体蒸馏或分馏物质的玻璃容器——蒸馏瓶,其底部是球形,球的半径为9 cm,瓶内液体的最大深度$CD=6cm$,则截面圆中的弦AB的长为$12\sqrt{2}$cm.

答案： $12\sqrt{2}$

10.已知$\odot O$的直径$CD=10$,弦$AB=8,AB⊥CD$,垂足为M,则DM的长为$2$或$8$.

答案： $2$或$8$

11.如图,AB是$\odot O$的弦,AB的长为8,P是$\odot O$上的一个点(不与点A,B重合),过点O作$OC⊥AP$于点C,$OD⊥PB$于点D,连接CD,则CD的长为 (D)
A.3
B.$2\sqrt {3}$
C.$4\sqrt {3}$
D.4

答案： D

12.已知$\odot O$的半径为7,AB为$\odot O$的弦,点P在弦AB上.若$PA=4,PB=6$,则OP的长为 (D)
A.$\sqrt {14}$
B.4
C.$\sqrt {23}$
D.5

答案： D

13.(2024·合肥包河区期末)如图,AB是$\odot O$的直径,弦CD交AB于点E,$BE=1,AE=5,∠AEC=30^{\circ }$,则CD的长为____$4\sqrt{2}$.

答案： $4\sqrt{2}$

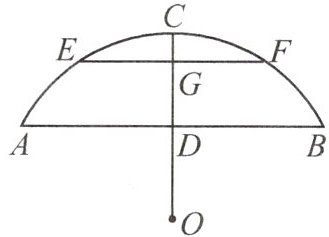
14.如图,某地有一座圆弧形拱桥,其圆心为点O,桥下水面宽度AB为7.2 m,拱高CD为2.4 m.
(1)求拱桥的半径;
(2)夏季雨季来临时,当水面离桥顶C的距离为1 m时,就要禁止通行,某天暴雨后桥下水面宽度EF为3 m,请通过计算说明是否要禁止通行.

答案： 【解析】：
### $(1)$求拱桥的半径
连接$OA$，设拱桥的半径为$r$米。
因为$CD$是拱高，所以$CD\perp AB$，由垂径定理可知$AD = \frac{1}{2}AB$（垂直于弦的直径平分弦）。
已知$AB = 7.2$米，则$AD=\frac{1}{2}\times7.2 = 3.6$米，$OD=(r - 2.4)$米。
在$Rt\triangle ADO$中，根据勾股定理$OA^{2}=AD^{2}+OD^{2}$，即$r^{2}=3.6^{2}+(r - 2.4)^{2}$。
展开$(r - 2.4)^{2}$得$r^{2}=3.6^{2}+r^{2}-4.8r + 2.4^{2}$。
移项可得$4.8r=3.6^{2}+2.4^{2}$，即$4.8r = 12.96 + 5.76$，$4.8r=18.72$，解得$r = 3.9$米。
### $(2)$判断是否要禁止通行
连接$OE$，已知$EF = 3$米，由垂径定理得$EG=\frac{1}{2}EF=\frac{1}{2}\times3 = 1.5$米。
设此时水面到圆心的距离为$OG$，已知$OE=r = 3.9$米。
在$Rt\triangle EGO$中，根据勾股定理$OG=\sqrt{OE^{2}-EG^{2}}$。
将$OE = 3.9$米，$EG = 1.5$米代入可得$OG=\sqrt{3.9^{2}-1.5^{2}}=\sqrt{(3.9 + 1.5)(3.9 - 1.5)}=\sqrt{5.4\times2.4}=\sqrt{12.96}=3.6$米。
此时水面离桥顶$C$的距离为$CG=OC - OG$，因为$OC=r = 3.9$米，所以$CG=3.9 - 3.6 = 0.3$米。
因为$0.3\lt1$，所以要禁止通行。
【答案】：
$(1)$拱桥的半径为$\boldsymbol{3.9}$米；$(2)$要禁止通行。

15.一次综合实践的主题为只用一张矩形纸条和一把刻度尺,如何测量一次性纸杯杯口的直径?小聪同学所在的学习小组想到了如下方法:如图,将纸条拉直并紧贴杯口,纸条的上下边沿分别与杯口相交于A,B,C,D四点.若用刻度尺量得该纸条的宽为4.25 cm,$AB=2.5cm,CD=6cm$.请你帮忙计算出纸杯的直径.

答案： 【解析】：
过圆心$O$作$OE\perp AB$于点$E$，延长$EO$交$CD$于点$F$，连接$OA$，$OC$。
因为$AB// CD$，$OE\perp AB$，所以$OF\perp CD$。
由垂径定理得$AE = \dfrac{1}{2}AB = \dfrac{1}{2}\times2.5 = 1.25cm$，$CF = \dfrac{1}{2}CD = \dfrac{1}{2}\times6 = 3cm$。
设$OE = x cm$，则$OF=(x + 4.25)cm$。
在$Rt\triangle OAE$中，$OA^{2}=AE^{2}+OE^{2}=1.25^{2}+x^{2}$；
在$Rt\triangle OCF$中，$OC^{2}=CF^{2}+OF^{2}=3^{2}+(x + 4.25)^{2}$。
因为$OA = OC$（都是圆的半径），所以$1.25^{2}+x^{2}=3^{2}+(x + 4.25)^{2}$。
展开得$1.5625+x^{2}=9+x^{2}+8.5x + 18.0625$。
移项得$8.5x=1.5625 - 9 - 18.0625$，即$8.5x=-25.5$，解得$x=-3$（长度不能为负，说明$E$在$AB$下方延长线上）。
则$OA^{2}=1.25^{2}+(-3)^{2}=1.5625 + 9 = 10.5625$，所以$OA = 3.25cm$。
那么纸杯的直径为$2OA = 6.5cm$。
【答案】：$6.5cm$