第78页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页

答案:
【解析】:本题主要考查旋转、中心对称等相关的基本概念。旋转的三要素是旋转中心、旋转方向和旋转角;根据旋转的性质,对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角,旋转前后的图形全等;中心对称的性质为对称点所连线段都经过对称中心,而且被对称中心所平分,中心对称的两个图形是全等图形;关于原点对称的点的坐标,横、纵坐标都互为相反数,所以点$P(x,y)$关于原点对称的点的坐标为$(-x,-y)$。
【答案】:①旋转中心;②旋转方向;③旋转角;④相等;⑤旋转角;⑥全等;⑦平分;⑧全等图形;⑨$(-x,-y)$
【答案】:①旋转中心;②旋转方向;③旋转角;④相等;⑤旋转角;⑥全等;⑦平分;⑧全等图形;⑨$(-x,-y)$
1.(2024·辽宁)纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是(

B
)
答案:
B
2.(2025·芜湖无为期中)已知点$A(2,m)$和点$B(n,-1)$关于原点对称,则$m+n=$(
A.1
B.-1
C.3
D.-3
B
)A.1
B.-1
C.3
D.-3
答案:
B
3.如图,将线段$AB$先向左平移,使点$B$与原点$O$重合,再将所得线段绕原点$O$旋转$180^{\circ}$得到线段$A'B'$,则点$A$的对应点$A'$的坐标是(
A.$(2,-3)$
B.$(-2,3)$
C.$(3,-2)$
D.$(-3,2)$
A
)A.$(2,-3)$
B.$(-2,3)$
C.$(3,-2)$
D.$(-3,2)$
答案:
A
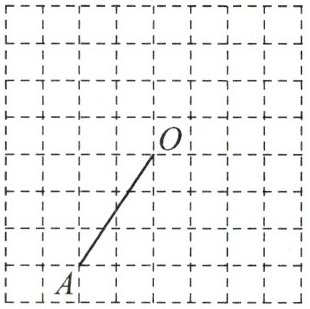
4.如图,在方格纸中按要求画图,并完成填空.
(1)画出线段$OA$绕点$O$顺时针旋转$90^{\circ}$后得到的线段$OB$,连接$AB$;
(2)画出与$\triangle AOB$关于$OB$对称的图形,点$A$的对称点是点$C$;
(3)填空:$\angle OCB$的度数为________.
(1)画出线段$OA$绕点$O$顺时针旋转$90^{\circ}$后得到的线段$OB$,连接$AB$;
(2)画出与$\triangle AOB$关于$OB$对称的图形,点$A$的对称点是点$C$;
(3)填空:$\angle OCB$的度数为________.

答案:
(1) 如图, OB, AB 即为所求.
(2) 如图,$\triangle COB$即为所求.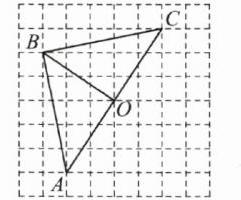
(3) 由旋转和对称的性质可知,$\triangle AOB\cong\triangle COB$,$\angle AOB = 90^{\circ}$,$OA = OC$,$OB = OB$。
因为$OA$绕点$O$顺时针旋转$90^{\circ}$得到$OB$,所以$\angle AOB = 90^{\circ}$,又因为$\triangle AOB$与$\triangle COB$关于$OB$对称,所以$\angle BOC=\angle BOA = 90^{\circ}$,且$OA = OC$,设方格边长为$1$,通过勾股定理可算出$OA=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,$OC = OA = 2\sqrt{2}$,$BC = AB=\sqrt{(2 + 2)^{2}+(2 - 2)^{2}} = 4$(利用方格计算线段长度),$\triangle OCB$中,$OB=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,根据勾股定理逆定理$OB^{2}+OC^{2}=(2\sqrt{2})^{2}+(2\sqrt{2})^{2}=16$,$BC^{2}=16$,所以$OB^{2}+OC^{2}=BC^{2}$,$\angle BOC = 90^{\circ}$,$OB = OC$,所以$\angle OCB = 45^{\circ}$。
【答案】:$45^{\circ}$
(1) 如图, OB, AB 即为所求.
(2) 如图,$\triangle COB$即为所求.

(3) 由旋转和对称的性质可知,$\triangle AOB\cong\triangle COB$,$\angle AOB = 90^{\circ}$,$OA = OC$,$OB = OB$。
因为$OA$绕点$O$顺时针旋转$90^{\circ}$得到$OB$,所以$\angle AOB = 90^{\circ}$,又因为$\triangle AOB$与$\triangle COB$关于$OB$对称,所以$\angle BOC=\angle BOA = 90^{\circ}$,且$OA = OC$,设方格边长为$1$,通过勾股定理可算出$OA=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,$OC = OA = 2\sqrt{2}$,$BC = AB=\sqrt{(2 + 2)^{2}+(2 - 2)^{2}} = 4$(利用方格计算线段长度),$\triangle OCB$中,$OB=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,根据勾股定理逆定理$OB^{2}+OC^{2}=(2\sqrt{2})^{2}+(2\sqrt{2})^{2}=16$,$BC^{2}=16$,所以$OB^{2}+OC^{2}=BC^{2}$,$\angle BOC = 90^{\circ}$,$OB = OC$,所以$\angle OCB = 45^{\circ}$。
【答案】:$45^{\circ}$
5.如图,在平面直角坐标系中,已知$\triangle ABC$的三个顶点的坐标分别是$A(1,1)$,$B(4,2)$,$C(3,5)$.
(1)以点$O$为旋转中心,将$\triangle ABC$逆时针旋转$90^{\circ}$,得到$\triangle A_{1}B_{1}C_{1}$,请画出$\triangle A_{1}B_{1}C_{1}$(点$A$,$B$,$C$的对应点分别为$A_{1}$,$B_{1}$,$C_{1}$);
(2)将$\triangle ABC$平移,使平移后点$B$,$C$的对应点$B_{2}$,$C_{2}$分别在$y$轴和$x$轴上,画出平移后的$\triangle A_{2}B_{2}C_{2}$;
(3)借助网格,请用无刻度的直尺画出$\triangle A_{2}B_{2}C_{2}$的中线$C_{2}D$.(保留作图辅助线)

(1)以点$O$为旋转中心,将$\triangle ABC$逆时针旋转$90^{\circ}$,得到$\triangle A_{1}B_{1}C_{1}$,请画出$\triangle A_{1}B_{1}C_{1}$(点$A$,$B$,$C$的对应点分别为$A_{1}$,$B_{1}$,$C_{1}$);
(2)将$\triangle ABC$平移,使平移后点$B$,$C$的对应点$B_{2}$,$C_{2}$分别在$y$轴和$x$轴上,画出平移后的$\triangle A_{2}B_{2}C_{2}$;
(3)借助网格,请用无刻度的直尺画出$\triangle A_{2}B_{2}C_{2}$的中线$C_{2}D$.(保留作图辅助线)

答案:
解:
(1) 如图,$\triangle A_{1}B_{1}C_{1}$即为所求.
(2) 如图,$\triangle A_{2}B_{2}C_{2}$即为所求.
(3) 如图, 线段$C_{2}D_{2}$即为所求.
解:
(1) 如图,$\triangle A_{1}B_{1}C_{1}$即为所求.
(2) 如图,$\triangle A_{2}B_{2}C_{2}$即为所求.
(3) 如图, 线段$C_{2}D_{2}$即为所求.

查看更多完整答案,请扫码查看


