第50页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1. (链接教材)已知一个直角三角形的两直角边的边长之和为20.设其中一条直角边的边长为x,则面积S关于x的函数解析式为
$S=-\frac{1}{2}x^{2}+10x$
,当x=10
时,S有最大值,最大值为50
.
答案:
$S=-\frac{1}{2}x^{2}+10x$;$10$;$50$
2. (2025·六安霍邱期中改编)一个长20m、宽16m的矩形花园如图所示,根据需要,计划将它的长缩短xm、宽增加xm,要想使修改后的花园面积达到最大,则x=
2
.
答案:
$2$
3. (2024·泰安)如图,小明的父亲想用长为60米的栅栏,再借助房屋的外墙围成一个矩形的菜园.已知房屋的外墙长40米,则可围成的菜园的最大面积是
450
平方米.
答案:
$450$
4. 如图,已知▱ABCD的周长为8cm,∠B=30°,设边长AB=xcm.
(1)▱ABCD的面积y(cm²)与x(cm)之间的函数解析式为
(2)当x=
(1)▱ABCD的面积y(cm²)与x(cm)之间的函数解析式为
$y =-\frac{1}{2}x^{2}+2x$
,自变量x的取值范围是$0\lt x\lt4$
;(2)当x=
2
时,y的值最大,最大值为2
.
答案:
(1)$y =-\frac{1}{2}x^{2}+2x$;$0\lt x\lt4$
(2)$2$;$2$
(1)$y =-\frac{1}{2}x^{2}+2x$;$0\lt x\lt4$
(2)$2$;$2$
5. (2025·合肥庐阳区月考)如图,现利用一面墙(a=12m),用总长为36m的篱笆围成中间隔有一道篱笆的矩形花圃ABCD.设花圃的一边AB的长为xm,面积为Sm².
(1)求S关于x的函数解析式及自变量x的取值范围.
(2)当AB的长是多少米时,围成的矩形花圃ABCD的面积最大?求出最大面积.

(1)求S关于x的函数解析式及自变量x的取值范围.
(2)当AB的长是多少米时,围成的矩形花圃ABCD的面积最大?求出最大面积.

答案:
【解析】:
(1)已知$AB = xm$,因为篱笆总长为$36m$,且中间隔有一道篱笆,所以$BC=(36 - 3x)m$。
根据矩形面积公式$S = AB\times BC$,可得$S=x(36 - 3x)=-3x^{2}+36x$。
又因为墙长$a = 12m$,所以$0\lt36 - 3x\leqslant12$,
解不等式$36 - 3x\gt0$,得$3x\lt36$,$x\lt12$;
解不等式$36 - 3x\leqslant12$,得$3x\geqslant36 - 12$,$3x\geqslant24$,$x\geqslant8$。
所以自变量$x$的取值范围是$8\leqslant x\lt12$。
(2)对于二次函数$S=-3x^{2}+36x$,其中$a=-3\lt0$,函数图象开口向下,对称轴为$x =-\frac{b}{2a}=-\frac{36}{2\times(-3)} = 6$。
因为对称轴$x = 6$不在自变量$x$的取值范围$8\leqslant x\lt12$内,且函数图象开口向下,在对称轴右侧$S$随$x$的增大而减小。
所以当$x = 8$时,$S$有最大值,$S=-3\times8^{2}+36\times8=-3\times64 + 288=-192 + 288 = 96$。
【答案】:
(1)$S=-3x^{2}+36x$,$8\leqslant x\lt12$;
(2)当$AB$的长是$8$米时,围成的矩形花圃$ABCD$的面积最大,最大面积是$96m^{2}$。
(1)已知$AB = xm$,因为篱笆总长为$36m$,且中间隔有一道篱笆,所以$BC=(36 - 3x)m$。
根据矩形面积公式$S = AB\times BC$,可得$S=x(36 - 3x)=-3x^{2}+36x$。
又因为墙长$a = 12m$,所以$0\lt36 - 3x\leqslant12$,
解不等式$36 - 3x\gt0$,得$3x\lt36$,$x\lt12$;
解不等式$36 - 3x\leqslant12$,得$3x\geqslant36 - 12$,$3x\geqslant24$,$x\geqslant8$。
所以自变量$x$的取值范围是$8\leqslant x\lt12$。
(2)对于二次函数$S=-3x^{2}+36x$,其中$a=-3\lt0$,函数图象开口向下,对称轴为$x =-\frac{b}{2a}=-\frac{36}{2\times(-3)} = 6$。
因为对称轴$x = 6$不在自变量$x$的取值范围$8\leqslant x\lt12$内,且函数图象开口向下,在对称轴右侧$S$随$x$的增大而减小。
所以当$x = 8$时,$S$有最大值,$S=-3\times8^{2}+36\times8=-3\times64 + 288=-192 + 288 = 96$。
【答案】:
(1)$S=-3x^{2}+36x$,$8\leqslant x\lt12$;
(2)当$AB$的长是$8$米时,围成的矩形花圃$ABCD$的面积最大,最大面积是$96m^{2}$。
6. (2024·淮北一模)如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是 (
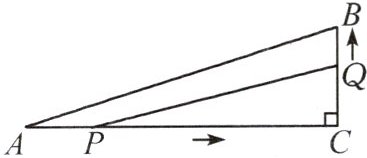
A. 20cm
B. 18cm
C. 2√5cm
D. 3√2cm
C
)
A. 20cm
B. 18cm
C. 2√5cm
D. 3√2cm
答案:
C
查看更多完整答案,请扫码查看


