《2025年一本九年级数学上册人教版安徽专版》

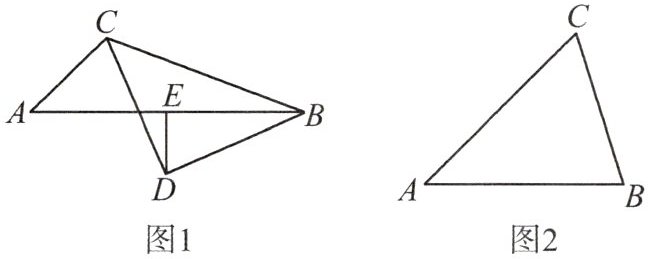
5. 在△ABC 中，∠A = 45°，∠ABC = α，以 BC 为斜边作等腰直角三角形 BDC，使得 A，D 两点在直线 BC 的同侧，过点 D 作 DE⊥AB 于点 E。
(1) 如图 1，当 α = 20°时，
① 求∠CDE 的度数；
② 判断线段 AE 与 BE 之间的数量关系，并说明理由。
(2) 若 45° ＜ α ＜ 90°，线段 AE 与 BE 之间的数量关系是否保持不变？依题意补全图 2，并写出证明过程。

答案： 【解析】：
### $(1)$ ① 求$\angle CDE$的度数
- 已知在$\triangle ABC$中，$\angle A = 45^{\circ}$，$\angle ABC=\alpha = 20^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle ACB=180^{\circ}-\angle A - \angle ABC=180^{\circ}-45^{\circ}-20^{\circ}=115^{\circ}$。
- 因为$\triangle BDC$是等腰直角三角形，所以$\angle BDC = 90^{\circ}$，$\angle DBC=\angle DCB = 45^{\circ}$，则$\angle ABD=\angle ABC+\angle DBC=20^{\circ}+45^{\circ}=65^{\circ}$。
- 由于$DE\perp AB$，所以$\angle DEB = 90^{\circ}$，在四边形$ACDE$中（可通过$\angle A+\angle ACB+\angle CDE+\angle DEB = 360^{\circ}$来计算$\angle CDE$），$\angle CDE=360^{\circ}-\angle A-\angle ACB-\angle DEB=360^{\circ}-45^{\circ}-115^{\circ}-90^{\circ}=110^{\circ}$。
### $(1)$ ② 判断线段$AE$与$BE$之间的数量关系
- 过点$D$作$DF\perp AC$交$AC$的延长线于点$F$。
因为$\angle A = 45^{\circ}$，$\angle DEB = 90^{\circ}$，$\angle DFC = 90^{\circ}$，$\angle DCB=\angle DBC = 45^{\circ}$，$\angle ACB + \angle FCD=180^{\circ}$，$\angle ACB = 115^{\circ}$，所以$\angle FCD = 65^{\circ}$，$\angle EBD = 65^{\circ}$。
又因为$DC = DB$，$\angle DFC=\angle DEB = 90^{\circ}$，根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等）可得$\triangle DFC\cong\triangle DEB$，所以$DF = DE$。
因为$\angle A = 45^{\circ}$，$\angle DFA = 90^{\circ}$，所以$\triangle ADF$是等腰直角三角形，$\angle A=\angle ADE = 45^{\circ}$，$AE = DE$。
又因为$DF = DE$，所以$AE = BE$。
### $(2)$ 当$45^{\circ}\lt\alpha\lt90^{\circ}$时，判断$AE$与$BE$的数量关系
过点$D$作$DF\perp AC$交$AC$的延长线于点$F$。
因为$\angle BDC = 90^{\circ}$，$DC = DB$，$\angle DFC=\angle DEB = 90^{\circ}$，$\angle DCF+\angle DCE = 180^{\circ}$，$\angle DBE+\angle DBC+\angle ABC = 180^{\circ}$，$\angle DBC = 45^{\circ}$，可得$\angle DCF=\angle DBE$。
根据$AAS$可得$\triangle DFC\cong\triangle DEB$，所以$DF = DE$。
因为$\angle A = 45^{\circ}$，$\angle DFA = 90^{\circ}$，所以$\angle A=\angle ADE = 45^{\circ}$，$AE = DE$（等腰直角三角形两腰相等）。
又因为$DF = DE$，所以$AE = BE$，即线段$AE$与$BE$之间的数量关系保持不变。
【答案】：
$(1)$ ①$\boldsymbol{110^{\circ}}$；②$\boldsymbol{AE = BE}$；$(2)$ 线段$AE$与$BE$之间的数量关系$\boldsymbol{AE = BE}$保持不变。

6. (选做)[问题提出]
(1) 如图 1，已知△ABC 为边长为 2 的等边三角形，则△ABC 的面积为 $\sqrt{3}$。
[问题探究]
(2). 如图 2，在△ABC 中，已知∠BAC = 120°，BC = 6$\sqrt{3}$，求△ABC 的最大面积。$27\sqrt{3}$
[问题解决]
(3). 如图 3，矩形 ABCD 是某校学生礼堂的平面示意图，其宽 AB = 20 米，长 BC = 24 米。为了能够监控到礼堂内部情况，现需要在礼堂最尾端墙面 CD 上安装一台摄像头 M 进行观测，并且要求能观测到礼堂前端墙面 AB 区域，同时为了观测效果达到最佳，还需要使观测角∠AMB = 45°。请你用所学知识进行分析，在 CD 区域上是否存在点 M 满足要求？若存在，求出 MC 的长度；若不存在，请说明理由。存在，MC 的长度为 8 米或 16 米

答案： 【解析】：
### $(1)$求等边$\triangle ABC$的面积
过$A$作$AD\perp BC$于$D$，因为$\triangle ABC$是等边三角形，$BC = 2$，所以$BD=\frac{1}{2}BC = 1$。
根据勾股定理$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。
根据三角形面积公式$S=\frac{1}{2}\times BC\times AD$，可得$S_{\triangle ABC}=\frac{1}{2}\times2\times\sqrt{3}=\sqrt{3}$。
### $(2)$求$\triangle ABC$的最大面积
以$BC$为弦作含$120^{\circ}$圆周角的弓形弧，当$A$为弓形弧的中点（$A$到$BC$距离最大）时，$\triangle ABC$面积最大。
过$A$作$AD\perp BC$于$D$，$O$为圆心，连接$OB$、$OC$。
因为$\angle BAC = 120^{\circ}$，所以$\angle BOC = 120^{\circ}$，又$OB = OC$，$BC = 6\sqrt{3}$，则$BD=\frac{1}{2}BC = 3\sqrt{3}$。
$\angle OBD = 30^{\circ}$，设$OD = x$，则$OB = 2x$，根据勾股定理$(2x)^{2}=x^{2}+(3\sqrt{3})^{2}$，解得$x = 3$，所以$AD = 9$。
根据三角形面积公式$S=\frac{1}{2}\times BC\times AD$，可得$S_{\triangle ABC}=\frac{1}{2}\times6\sqrt{3}\times9 = 27\sqrt{3}$。
### $(3)$判断$CD$区域上是否存在点$M$满足要求并求$MC$的长度
以$AB$为斜边在矩形$ABCD$外作等腰直角三角形$AEB$，$\angle AEB = 90^{\circ}$，$AE = BE$，过$E$作$EF\perp AB$于$F$，则$EF = AF = BF = 10$。
以$E$为圆心，$EA$为半径作圆，$EA=\sqrt{10^{2}+10^{2}} = 10\sqrt{2}$。
设$MC = x$，则$MD = 24 - x$。
根据圆周角定理，若$\angle AMB = 45^{\circ}$，则点$M$在$\odot E$上。
根据勾股定理$EM^{2}=EA^{2}=10^{2}+10^{2}=200$，$EM^{2}=(x - 10)^{2}+(20)^{2}$或$EM^{2}=(10-(24 - x))^{2}+20^{2}$。
即$(x - 10)^{2}+400 = 200$（无解）或$(x - 14)^{2}+400 = 200$（无解），以$AB$为斜边在矩形$ABCD$内作等腰直角三角形$AEB$， 过$E$作$EF\perp AB$于$F$，$EF = AF = BF = 10$，$EA=\sqrt{10^{2}+10^{2}} = 10\sqrt{2}$。
设$MC=x$，根据勾股定理$EM^{2}=(x + 10)^{2}+20^{2}$，因为$\angle AMB = 45^{\circ}$，点$M$在$\odot E$上，$EM = EA = 10\sqrt{2}$，则$(x + 10)^{2}+400=(10\sqrt{2})^{2}$（无解）；再以$AB$为边向上作等边三角形$ABF$，作$\triangle ABF$的外接圆$\odot O$，过$O$作$OH\perp AB$于$H$，$AH = 10$，$\angle AOH = 60^{\circ}$，$OA=\frac{20\sqrt{3}}{3}$。
设$MC = x$，根据勾股定理$OM^{2}=(x - 10)^{2}+20^{2}$，因为$\angle AMB = 45^{\circ}$，$\angle AOB = 120^{\circ}$，根据正弦定理$\frac{AB}{\sin\angle AMB}=2R$（$R$为$\triangle AMB$外接圆半径），$2R=\frac{20}{\sin45^{\circ}} = 20\sqrt{2}$。
设$M$坐标为$(x,20)$，$A(0,0)$，$B(20,0)$，根据两点间距离公式$MA^{2}=x^{2}+20^{2}$，$MB^{2}=(20 - x)^{2}+20^{2}$，再根据余弦定理$\cos\angle AMB=\frac{MA^{2}+MB^{2}-AB^{2}}{2MA\cdot MB}=\frac{\sqrt{2}}{2}$。
$\begin{aligned}\frac{x^{2}+400+(20 - x)^{2}+400 - 400}{2\sqrt{(x^{2}+400)[(20 - x)^{2}+400]}}&=\frac{\sqrt{2}}{2}\\\frac{x^{2}-20x + 800}{ \sqrt{(x^{2}+400)[(20 - x)^{2}+400]}}&=\sqrt{2}\\(x^{2}-20x + 800)^{2}&=2(x^{2}+400)[(20 - x)^{2}+400]\\x^{4}-40x^{3}+2000x^{2}-16000x + 640000&=2(x^{4}-40x^{3}+1200x^{2}-16000x + 320000)\\x^{4}-40x^{3}+2000x^{2}-16000x + 640000&=2x^{4}-80x^{3}+2400x^{2}-32000x + 640000\\x^{4}-40x^{3}+400x^{2}-16000x&=0\\x(x^{3}-40x^{2}+400x - 16000)&=0\\x(x - 16)(x^{2}-24x + 1000)&=0\end{aligned}$
解得$x = 16$或$x = 8$。
【答案】：
$(1)$$\boldsymbol{\sqrt{3}}$；
$(2)$$\boldsymbol{27\sqrt{3}}$；
$(3)$存在，$MC$的长度为$\boldsymbol{8}$米或$\boldsymbol{16}$米。