《2025年一本九年级数学上册人教版安徽专版》

10.用反证法证明“若$\odot O$的半径为$r$，点$P$到圆心的距离$d ＜ r$，则点$P$在$\odot O$的内部”，首先应假设（D）
A.$d\leqslant r$
B.$d\geqslant r$
C.点$P$在$\odot O$的外部
D.点$P$在$\odot O$上或$\odot O$的外部

答案： D

11.已知点$P$与某圆上的点之间的最小距离为6 cm，最大距离为16 cm，则该圆的半径为$5cm$或$11cm$.

答案： $5cm$或$11cm$

12.(2025·淮北期末)如图，在$Rt\triangle ABC$中，$∠ACB = 90^{\circ}$，$AC = 6$，$BC = 8$，$CP$，$CM$分别是$AB$上的高线和中线.如果$\odot A$是以点$A$为圆心，4为半径的圆，那么下列判断中，正确的是（C）

A.点$P$，$M$均在$\odot A$内
B.点$P$，$M$均在$\odot A$外
C.点$P$在$\odot A$内，点$M$在$\odot A$外
D.以上选项都不正确

答案： C

13.如图，在矩形$ABCD$中，$AB = 4$，$AD = 3$，以顶点$D$为圆心作半径为$r$的圆.若要求另外三个顶点$A$，$B$，$C$中至少有一个点在圆内，且至少有一个点在圆外，则$r$的取值范围是$3\lt r\lt5$.

答案： $3\lt r\lt5$

14.如图，在$\triangle ABC$中，$∠A = 60^{\circ}$，$BC = 5cm$，能够将$\triangle ABC$完全覆盖的最小圆形纸片的直径是$\frac{10\sqrt{3}}{3}$cm.

答案： $\frac{10\sqrt{3}}{3}$

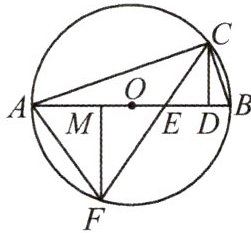
15.(2024·安徽)如图，$\odot O$是$\triangle ABC$的外接圆，$D$是直径$AB$上的一点，$∠ACD$的平分线交$AB$于点$E$，交$\odot O$于另一点$F$，$FA = FE$.
(1)求证：$CD⊥AB$；
(2)作$FM⊥AB$，垂足为$M$，若$OM = OE = 1$，求$AC$的长.

答案： 解:
(1)证明:$\because FA=FE,\therefore ∠FAE=∠AEF.$ $\because ∠FAE$与$∠BCE$都是$\widehat {BF}$所对的圆周角, $\therefore ∠FAE=∠BCE,\therefore ∠AEF=∠BCE.$ $\because ∠AEF=∠CEB,\therefore ∠CEB=∠BCE.$ $\because CE$平分$∠ACD,\therefore ∠ACE=∠DCE.$ $\because AB$是直径,$\therefore ∠ACB=90^{\circ },$ $\therefore ∠CEB+∠DCE=∠BCE+∠ACE=∠ACB=90^{\circ },$ $\therefore ∠CDE=90^{\circ },\therefore CD⊥AB.$
(2)$AC=4\sqrt {2}$ 

16.(1)如图，已知$OA = OB = OC$，$∠ACB = 28^{\circ}$，则$∠AOB$的度数是$56^{\circ}$.

答案： $56^{\circ}$

(2)如图，点$A$，$B$的坐标分别为$(6,0)$，$(0,8)$，$C$为坐标平面内的一点，$BC = 1$，$M$为线段$AC$的中点，连接$OM$，则$OM$的最大值为$\dfrac{11}{2}$，$OM$的最小值为$\dfrac{9}{2}$.

答案： $\dfrac{11}{2}$，$\dfrac{9}{2}$