《2025年学霸题中题九年级数学上册人教版》

9.(雅安中考)在平面直角坐标系中,点$(a+2,2)$关于原点的对称点为$(4,-b)$,则$ab$的值为______−12。

答案： −12

10. 如图,将$\triangle ABC绕点A逆时针旋转150^{\circ}$,得到$\triangle ADE$,这时点$B$,$C$,$D$恰好在同一条直线上,则$∠B$的度数为______15°。

答案： 15°

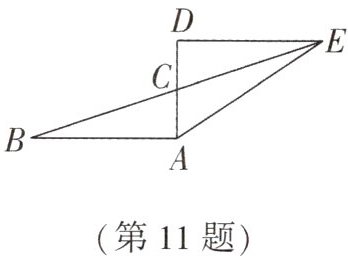
11.(信阳中考)如图,已知$AB= 3$,$AC= 1$,$∠D= 90^{\circ}$,$\triangle DEC与\triangle ABC关于点C$成中心对称,则$AE$的长是______$\sqrt{13}$。

答案： $\sqrt{13}$

12.(烟台中考改编)如图,$A点的坐标为(-1,5)$,$B点的坐标为(3,3)$,$C点的坐标为(5,3)$,$D点的坐标为(3,-1)$,小明发现：线段$AB与线段CD$存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是______(1,1)或(4,4)。

答案： (1,1)或(4,4)

13.(2023·宿迁中考)如图,$\triangle ABC$是正三角形,点$A$在第一象限,点$B(0,0)$、$C(1,0)$。将线段$CA绕点C按顺时针方向旋转120^{\circ}至CP_{1}$；将线段$BP_{1}绕点B按顺时针方向旋转120^{\circ}至BP_{2}$；将线段$AP_{2}绕点A按顺时针方向旋转120^{\circ}至AP_{3}$；将线段$CP_{3}绕点C按顺时针方向旋转120^{\circ}至CP_{4}$……以此类推,则点$P_{99}$的坐标是______。

答案：
(−49,50√3) 解析:如图①所示,由图象可得,点$P_{1},P_{4}$在$x$轴的正半轴上,
∴旋转3次为一个循环.
∵99÷3 = 33,
∴点$P_{99}$在射线CA的延长线上,
∴点$P_{100}$在x轴的正半轴上.
∵C(1,0),△ABC是正三角形,
∴由旋转的性质可得,AC = CP₁ = 1,
∴BP₁ = OC + CP₁ = 2,
∴P₁(2,0),
∴BP₂ = BP₁ = 2,
∴AP₃ = AP₂ = OP₂ + AO = 3,
∴CP₄ = CP₃ = CA + AP₃ = 1 + 3 = 4,
∴BP₄ = BC + CP₄ = 5,
∴P₄(5,0),同理可得,P₇(8,0),P₁₀(11,0),
∴P₁₀₀(101,0),
∴BP₁₀₀ = 101,
∴CP₁₀₀ = 101 - 1 = 100,
∴由旋转的性质可得,CP₉₉ = 100.如图②所示,过点$P_{99}$作$P_{99}E\perp x$轴于点E,
∵∠ACB = 60°,
∴∠$EP_{99}C$ = 30°,
∴EC = $\frac{1}{2}$$P_{99}C$ = 50,
∴EO = EC - OC = 49,$P_{99}E$ = $\sqrt{P_{99}C^{2} - EC^{2}}$ = 50√3,
∴点$P_{99}$的坐标是(−49,50√3).

14.(2024·盐城中考)如图,在$\triangle ABC$中,$∠ACB= 90^{\circ}$,$AC= BC= 2\sqrt{2}$,点$D是AC$的中点,连接$BD$,将$\triangle BCD绕点B$旋转,得到$\triangle BEF$。连接$CF$,当$CF// AB$时,$CF= $______。

答案：
2 + $\sqrt{6}$或$\sqrt{6}$ - 2 解析:
∵在△ABC中,∠ACB = 90°,AC = BC = 2$\sqrt{2}$,
∴∠CAB = ∠CBA = 45°,AB = $\sqrt{2}$AC = 4.
∵点D是AC的中点,
∴AD = CD = $\frac{1}{2}$AC = $\sqrt{2}$,
∴在Rt△BCD中,BD = $\sqrt{CD^{2} + BC^{2}}$ = $\sqrt{(\sqrt{2})^{2} + (2\sqrt{2})^{2}}$ = $\sqrt{10}$.
∵将△BCD绕点B旋转得到△BEF,
∴△BCD≌△BEF,
∴BD = BF = $\sqrt{10}$,EF = CD = $\sqrt{2}$,BC = BE = 2$\sqrt{2}$.分情况讨论:如图①所示,过点B作BG⊥CF,垂足为G,
∵CF//AB,
∴∠FCB = ∠CBA = 45°,
∴△BCG是等腰直角三角形,且BC = 2$\sqrt{2}$,
∴CG = BG = $\frac{\sqrt{2}}{2}$BC = $\frac{\sqrt{2}}{2}$×2$\sqrt{2}$ = 2.在Rt△BFG中,FG = $\sqrt{BF^{2} - BG^{2}}$ = $\sqrt{(\sqrt{10})^{2} - 2^{2}}$ = $\sqrt{6}$,
∴CF = CG + FG = 2 + $\sqrt{6}$;如图②所示,当点D运动到点$F'$时,此时$CF'// AB$,同理可得,$GF'$ = $\sqrt{6}$,$CG = 2$,
∴$CF'$ = $\sqrt{6}$ - 2.

15.(12分)(临沂中考改编)将矩形$ABCD绕点A顺时针旋转\alpha(0^{\circ}＜\alpha＜180^{\circ})$,得到矩形$AEFG$。
(1)如图,当点$E在BD$上时,求证：$FD= CD$。
(2)当$\alpha$为何值时,$GC= GB$？画出图形,并说明理由。

答案：

(1) 由旋转可得,AE = AB,∠AEF = ∠ABC = ∠DAB = 90°,EF = BC = AD,
∴∠AEB = ∠ABE.又
∵∠ABE + ∠EDA = 90° = ∠AEB + ∠DEF,
∴∠EDA = ∠DEF.又
∵DE = ED,
∴△AED≌△FDE,
∴AE = FD.又
∵AE = AB = CD,
∴FD = CD.
(2) 如图,当α = 60°时,GC = GB,理由如下:取BC的中点H,连接GH交AD于点M,连接GD.
∵GC = GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM = BH = $\frac{1}{2}$AD = $\frac{1}{2}$AG,
∴GM垂直平分AD,
∴GD = GA = DA,
∴△ADG是等边三角形,
∴∠DAG = 60°,
∴旋转角α = 60°.

16.(12分)(武汉中考)如图是由小正方形组成的$9×6$网格,每个小正方形的顶点叫做格点。$\triangle ABC$的三个顶点都是格点。仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示。
(1)在图①中,$D$,$E分别是边AB$,$AC$与网格线的交点。先将点$B绕点E旋转180^{\circ}得到点F$,画出点$F$,再在$AC上画点G$,使$DG// BC$；
(2)在图②中,$P是边AB$上一点,$∠BAC= \alpha$。先将$AB绕点A逆时针旋转2\alpha$,得到线段$AH$,画出线段$AH$,再画点$Q$,使$P$,$Q两点关于直线AC$对称。

答案：

(1) 如图①所示,点F,点G即为所求.
(2) 如图②所示,线段AH,点Q即为所求.