第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
7. (潍坊中考)如图,有一块边长为6 cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是 (
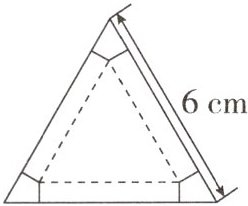
A. $\sqrt{3}$ cm^2
B. $\frac{3\sqrt{3}}{2}$ cm^2
C. $\frac{9\sqrt{3}}{2}$ cm^2
D. $\frac{27\sqrt{3}}{2}$ cm^2
C
)
A. $\sqrt{3}$ cm^2
B. $\frac{3\sqrt{3}}{2}$ cm^2
C. $\frac{9\sqrt{3}}{2}$ cm^2
D. $\frac{27\sqrt{3}}{2}$ cm^2
答案:
C
8. (淮安中考)如图①,△ABC和△A'B'C'是两个边长不相等的等边三角形,点B',C',B,C都在直线l上,△ABC固定不动,将△A'B'C'在直线l上自左向右平移.开始时,点C'与点B重合,当点B'移动到与点C重合时停止.设△A'B'C'移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图②所示,则△ABC的边长是______

5
.
答案:
5
9. 如图,在Rt△ABC中,∠BAC = 90°,AB = AC = 2$\sqrt{2}$,AD为BC边上的高,动点P在AD上(不与点A,D重合),从点A出发,沿A→D方向运动,设AP = x,△ABP的面积为S_1,矩形PDFE的面积为S_2,y = S_1 + S_2,则y与x的解析式是
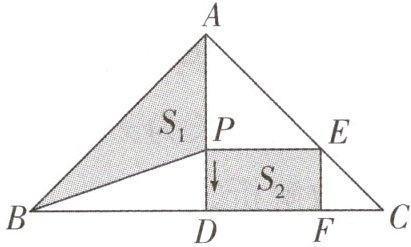
y = -x² + 3x(0 < x < 2)
.
答案:
y = -x² + 3x(0 < x < 2) 解析:
∵在Rt△ABC中,∠BAC = 90°,AB = AC = 2√2,AD为BC边上的高,AP = x,
∴∠BAD = ∠CAD = 45°,BC = 4,AD = BD = 2,
∴AP = PE = x,PD = AD - AP = 2 - x,
∴y = S₁ + S₂ = x + (2 - x)·x = -x² + 3x(0 < x < 2)。
∵在Rt△ABC中,∠BAC = 90°,AB = AC = 2√2,AD为BC边上的高,AP = x,
∴∠BAD = ∠CAD = 45°,BC = 4,AD = BD = 2,
∴AP = PE = x,PD = AD - AP = 2 - x,
∴y = S₁ + S₂ = x + (2 - x)·x = -x² + 3x(0 < x < 2)。
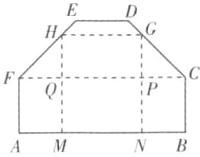
10. (2023·潍坊中考)工匠师傅准备从六边形的铁皮ABCDEF中,裁出一块矩形铁皮制作工件,如图所示.经测量,AB // DE,AB与DE之间的距离为2米,AB = 3米,AF = BC = 1米,∠A = ∠B = 90°,∠C = ∠F = 135°.MH,HG,GN是工匠师傅画出的裁剪虚线.当MH的长度为多少时,矩形铁皮MNGH的面积最大,最大面积是多少?


答案:
如图,连接CF,交MH于点Q,交NG于点P。
∵AF = BC = 1米,∠A = ∠B = 90°,
∴四边形ABCF是矩形。
∵四边形MNGH是矩形,
∴∠HMN = ∠MNG = 90°,MH = NG,
∴∠HQF = ∠GPC = 90°,MQ = AF = NP = BC = 1米。
∵∠BCG = ∠AFH = 135°,
∴∠HFQ = ∠GCP = 45°,
∴FQ = HQ,CP = GP,
∴FQ = HQ = MH - MQ = MH - 1。同理得CP = MH - 1,
∴AM = NB = MH - 1,
∴MN = AB - AM - NB = 3 - (MH - 1) - (MH - 1) = 5 - 2MH,
∴S矩形MNGH = MN·MH = (5 - 2MH)·MH = 5MH - 2MH² = -2(MH² - $\frac{5}{2}$MH) = -2(MH - $\frac{5}{4}$)² + $\frac{25}{8}$,
∴当MH = $\frac{5}{4}$米时,铁皮MNGH的面积最大,最大面积为$\frac{25}{8}$平方米。
如图,连接CF,交MH于点Q,交NG于点P。
∵AF = BC = 1米,∠A = ∠B = 90°,
∴四边形ABCF是矩形。

∵四边形MNGH是矩形,
∴∠HMN = ∠MNG = 90°,MH = NG,
∴∠HQF = ∠GPC = 90°,MQ = AF = NP = BC = 1米。
∵∠BCG = ∠AFH = 135°,
∴∠HFQ = ∠GCP = 45°,
∴FQ = HQ,CP = GP,
∴FQ = HQ = MH - MQ = MH - 1。同理得CP = MH - 1,
∴AM = NB = MH - 1,
∴MN = AB - AM - NB = 3 - (MH - 1) - (MH - 1) = 5 - 2MH,
∴S矩形MNGH = MN·MH = (5 - 2MH)·MH = 5MH - 2MH² = -2(MH² - $\frac{5}{2}$MH) = -2(MH - $\frac{5}{4}$)² + $\frac{25}{8}$,
∴当MH = $\frac{5}{4}$米时,铁皮MNGH的面积最大,最大面积为$\frac{25}{8}$平方米。
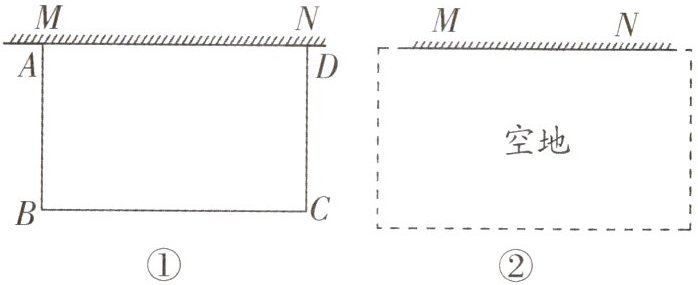
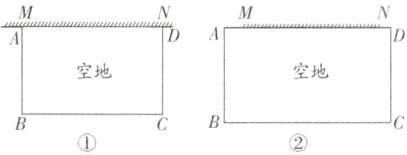
11. 教材P57复习题T7变式 (福建中考)空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a = 20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图①,求所利用旧墙AD的长;
(2)已知0 < a < 50,且空地足够大,如图②.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
(1)已知a = 20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图①,求所利用旧墙AD的长;
(2)已知0 < a < 50,且空地足够大,如图②.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.

答案:
(1) 设AD = x米,则AB = $\frac{100 - x}{2}$米,依题意,得$\frac{x(100 - x)}{2} = 450$,解得x₁ = 10,x₂ = 90。
∵a = 20,且x ≤ a,
∴x = 90不合题意,应舍去,
∴利用旧墙AD的长为10米。
(2) 设AD = x米,矩形ABCD的面积为S平方米。
① 如果按图①方案围成矩形菜园,依题意,得S = $\frac{x(100 - x)}{2} = -\frac{1}{2}(x - 50)^{2} + 1250$,0 < x < a。
∵0 < a < 50,
∴当x < a < 50时,S随x的增大而增大,当x = a时,S最大 = 50a - $\frac{1}{2}$a²。
② 如果按图②方案围成矩形菜园,依题意,得S = $\frac{x(100 + a - 2x)}{2} = -[x - (25 + \frac{a}{4})]^{2} + (25 + \frac{a}{4})^{2}$,a ≤ x < 50 + $\frac{a}{2}$,当a < 25 + $\frac{a}{4}$ < 50 + $\frac{a}{2}$,即0 < a < $\frac{100}{3}$时,则x = 25 + $\frac{a}{4}$时,S最大 = (25 + $\frac{a}{4}$)² = $\frac{10000 + 200a + a²}{16}$,当25 + $\frac{a}{4}$ ≤ a < 50,即$\frac{100}{3}$ ≤ a < 50时,S随x的增大而减小,
∴当x = a时,S最大 = $\frac{a(100 + a - 2a)}{2} = 50a - \frac{1}{2}a^{2}$。
综合①②,当0 < a < $\frac{100}{3}$时,$\frac{10000 + 200a + a^{2}}{16} - (50a - \frac{1}{2}a^{2}) = \frac{(3a - 100)^{2}}{16} > 0$,即$\frac{10000 + 200a + a^{2}}{16} > 50a - \frac{1}{2}a^{2}$,此时,按图②方案围成的矩形菜园面积最大,最大面积为$\frac{10000 + 200a + a^{2}}{16}$平方米。当$\frac{100}{3}$ ≤ a < 50时,两种方案围成的矩形菜园面积最大值相等。
∴当0 < a < $\frac{100}{3}$时,围成长和宽均为(25 + $\frac{a}{4}$)米的矩形菜园时面积最大,最大面积为$\frac{10000 + 200a + a^{2}}{16}$平方米;当$\frac{100}{3}$ ≤ a < 50时,围成长为a米,宽为(50 - $\frac{a}{2}$)米的矩形菜园时面积最大,最大面积为(50a - $\frac{1}{2}a^{2}$)平方米。
(1) 设AD = x米,则AB = $\frac{100 - x}{2}$米,依题意,得$\frac{x(100 - x)}{2} = 450$,解得x₁ = 10,x₂ = 90。
∵a = 20,且x ≤ a,
∴x = 90不合题意,应舍去,
∴利用旧墙AD的长为10米。
(2) 设AD = x米,矩形ABCD的面积为S平方米。
① 如果按图①方案围成矩形菜园,依题意,得S = $\frac{x(100 - x)}{2} = -\frac{1}{2}(x - 50)^{2} + 1250$,0 < x < a。
∵0 < a < 50,
∴当x < a < 50时,S随x的增大而增大,当x = a时,S最大 = 50a - $\frac{1}{2}$a²。

② 如果按图②方案围成矩形菜园,依题意,得S = $\frac{x(100 + a - 2x)}{2} = -[x - (25 + \frac{a}{4})]^{2} + (25 + \frac{a}{4})^{2}$,a ≤ x < 50 + $\frac{a}{2}$,当a < 25 + $\frac{a}{4}$ < 50 + $\frac{a}{2}$,即0 < a < $\frac{100}{3}$时,则x = 25 + $\frac{a}{4}$时,S最大 = (25 + $\frac{a}{4}$)² = $\frac{10000 + 200a + a²}{16}$,当25 + $\frac{a}{4}$ ≤ a < 50,即$\frac{100}{3}$ ≤ a < 50时,S随x的增大而减小,
∴当x = a时,S最大 = $\frac{a(100 + a - 2a)}{2} = 50a - \frac{1}{2}a^{2}$。
综合①②,当0 < a < $\frac{100}{3}$时,$\frac{10000 + 200a + a^{2}}{16} - (50a - \frac{1}{2}a^{2}) = \frac{(3a - 100)^{2}}{16} > 0$,即$\frac{10000 + 200a + a^{2}}{16} > 50a - \frac{1}{2}a^{2}$,此时,按图②方案围成的矩形菜园面积最大,最大面积为$\frac{10000 + 200a + a^{2}}{16}$平方米。当$\frac{100}{3}$ ≤ a < 50时,两种方案围成的矩形菜园面积最大值相等。
∴当0 < a < $\frac{100}{3}$时,围成长和宽均为(25 + $\frac{a}{4}$)米的矩形菜园时面积最大,最大面积为$\frac{10000 + 200a + a^{2}}{16}$平方米;当$\frac{100}{3}$ ≤ a < 50时,围成长为a米,宽为(50 - $\frac{a}{2}$)米的矩形菜园时面积最大,最大面积为(50a - $\frac{1}{2}a^{2}$)平方米。
查看更多完整答案,请扫码查看


