第118页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
9. (南京中考)如图,在平面直角坐标系中,点P在第一象限,$\odot P$与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若$\odot P$的半径为5,点A的坐标是$(0,8)$,则点D的坐标是 (

A. $(9,2)$
B. $(9,3)$
C. $(10,2)$
D. $(10,3)$
A
)
A. $(9,2)$
B. $(9,3)$
C. $(10,2)$
D. $(10,3)$
答案:
A
10. (贵阳中考)小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是______.


答案:
$\frac{4\sqrt{3}}{3}$ 解析:如图,当圆心$O$移动到点$P$的位置时,光盘再次与$AB$相切,切点为$Q$,连接$ON$,$PQ$,$OP$,其中$OP$与$AB$相交于点$H$.$\because ON⊥AB$,$PQ⊥AB$,$\therefore ON// PQ$.$\because ON=PQ$,易得$OH=PH$.在$Rt\triangle PHQ$中,$∠P=∠A=30^{\circ}$,$PQ=1$,$\therefore PH=\frac{2\sqrt{3}}{3}$,则$OP=\frac{4\sqrt{3}}{3}$.

$\frac{4\sqrt{3}}{3}$ 解析:如图,当圆心$O$移动到点$P$的位置时,光盘再次与$AB$相切,切点为$Q$,连接$ON$,$PQ$,$OP$,其中$OP$与$AB$相交于点$H$.$\because ON⊥AB$,$PQ⊥AB$,$\therefore ON// PQ$.$\because ON=PQ$,易得$OH=PH$.在$Rt\triangle PHQ$中,$∠P=∠A=30^{\circ}$,$PQ=1$,$\therefore PH=\frac{2\sqrt{3}}{3}$,则$OP=\frac{4\sqrt{3}}{3}$.

11. (南京中考)如图,已知P是$\odot O$外一点.用两种不同的方法过点P作$\odot O$的一条切线.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.

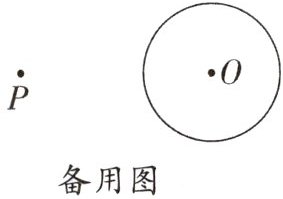


答案:
答案不唯一,示例:方法一:如图①,连接$OP$,作$OP$的垂直平分线,交$OP$于点$A$,再以点$A$为圆心,$PA$长为半径画圆,交$\odot O$于点$B$,连接$PB$,直线$PB$即为所求.
方法二:如图②,连接$OP$,交$\odot O$于点$C$;以点$O$为圆心,$OP$长为半径作圆;过点$C$作直线$CD⊥OP$,交大圆于点$D$;连接$OD$,交小圆于点$E$;连接$PE$,直线$PE$即为所求.
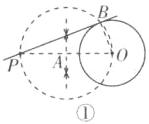
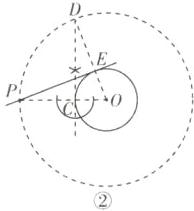
一题多解
方法三:如图③,作点$P$关于点$O$的对称点$P'$,以点$O$为圆心,$PO$长为半径作$\odot O$,连接$PP'$,设原来的$\odot O$半径为$r$,以$AB$(即$2r$)的长度为半径,$P'$为圆心画圆,交$\overset{\frown}{PP'}$于点$Q$,连接$PQ$,交原来的$\odot O$于点$D$,点$D$即为切点.(利用中位线能证明$OD$是半径且垂直于$PQ$)

答案不唯一,示例:方法一:如图①,连接$OP$,作$OP$的垂直平分线,交$OP$于点$A$,再以点$A$为圆心,$PA$长为半径画圆,交$\odot O$于点$B$,连接$PB$,直线$PB$即为所求.
方法二:如图②,连接$OP$,交$\odot O$于点$C$;以点$O$为圆心,$OP$长为半径作圆;过点$C$作直线$CD⊥OP$,交大圆于点$D$;连接$OD$,交小圆于点$E$;连接$PE$,直线$PE$即为所求.


一题多解
方法三:如图③,作点$P$关于点$O$的对称点$P'$,以点$O$为圆心,$PO$长为半径作$\odot O$,连接$PP'$,设原来的$\odot O$半径为$r$,以$AB$(即$2r$)的长度为半径,$P'$为圆心画圆,交$\overset{\frown}{PP'}$于点$Q$,连接$PQ$,交原来的$\odot O$于点$D$,点$D$即为切点.(利用中位线能证明$OD$是半径且垂直于$PQ$)

12. 阅读资料:我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角,如图①中$∠PAB$所示.同学们研究发现:P为圆上任意一点,若弦AC经过圆心O,且AB切$\odot O$于点A,此时弦切角$∠CAB= ∠P$(如图②).
证明:$\because AB切\odot O$于点A,$\therefore ∠CAB= 90^{\circ }$.又$\because AC$是直径,$\therefore ∠P= 90^{\circ },\therefore ∠CAB= ∠P$.
问题拓展:若AC不经过圆心O,如图③,当圆心O在$∠PCA$的内部时,$∠CAB= ∠P$还成立吗? 如图④,当圆心O在$∠PCA$的外部时,$∠CAB= ∠P$还成立吗? 请说明理由.
知识运用:如图⑤,AD是$△ABC中∠BAC$的平分线,经过点A的$\odot O$与BC相切于点D,与AB,AC分别相交于E,F.求证:$EF// BC$.
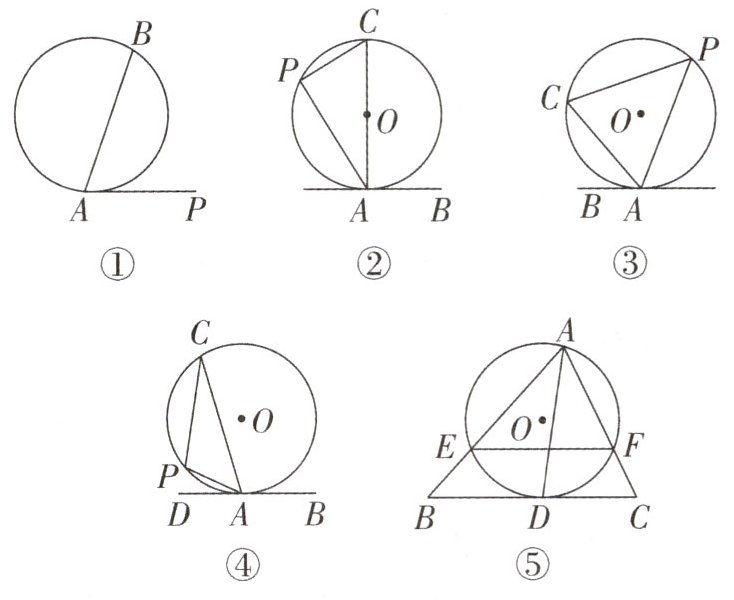
证明:$\because AB切\odot O$于点A,$\therefore ∠CAB= 90^{\circ }$.又$\because AC$是直径,$\therefore ∠P= 90^{\circ },\therefore ∠CAB= ∠P$.
问题拓展:若AC不经过圆心O,如图③,当圆心O在$∠PCA$的内部时,$∠CAB= ∠P$还成立吗? 如图④,当圆心O在$∠PCA$的外部时,$∠CAB= ∠P$还成立吗? 请说明理由.
知识运用:如图⑤,AD是$△ABC中∠BAC$的平分线,经过点A的$\odot O$与BC相切于点D,与AB,AC分别相交于E,F.求证:$EF// BC$.

答案:
问题拓展:当圆心$O$在$∠PCA$的内部时,$∠CAB=∠P$成立.理由如下:作直径$AD$,连接$CD$,如图①,则$∠D=∠P$,$\because AD$为直径,$\therefore ∠ACD=90^{\circ}$,$\therefore ∠D+∠CAD=90^{\circ}$.$\because AB$切$\odot O$于点$A$,$\therefore AD⊥AB$,$\therefore ∠CAB+∠CAD=90^{\circ}$,$\therefore ∠CAB=∠D=∠P$.当圆心$O$在$∠PCA$的外部时,$∠CAB=∠P$成立.理由如下:连接$AO$并延长交$\odot O$于点$D'$,连接$PD'$,如图②,由题干可知$∠PAD=∠D'$,$\because ∠C=∠D'$,$\therefore ∠PAD=∠PCA$.又$\because ∠C+∠CPA+∠CAP=180^{\circ}$,$∠PAD+∠PAC+∠CAB=180^{\circ}$,$\therefore ∠CAB=∠CPA$.

知识运用:如图③,连接$DF$,$\because AD$是$\triangle ABC$中$∠BAC$的平分线,$\therefore ∠BAD=∠CAD$.$\because$ 经过点$A$的$\odot O$与$BC$相切于点$D$,$\therefore ∠CDF=∠CAD$,$\therefore ∠BAD=∠CDF$.$\because ∠BAD=∠DFE$,$\therefore ∠CDF=∠DFE$,$\therefore EF// BC$.
归纳总结
(1)弦切角的定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
(2)弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
问题拓展:当圆心$O$在$∠PCA$的内部时,$∠CAB=∠P$成立.理由如下:作直径$AD$,连接$CD$,如图①,则$∠D=∠P$,$\because AD$为直径,$\therefore ∠ACD=90^{\circ}$,$\therefore ∠D+∠CAD=90^{\circ}$.$\because AB$切$\odot O$于点$A$,$\therefore AD⊥AB$,$\therefore ∠CAB+∠CAD=90^{\circ}$,$\therefore ∠CAB=∠D=∠P$.当圆心$O$在$∠PCA$的外部时,$∠CAB=∠P$成立.理由如下:连接$AO$并延长交$\odot O$于点$D'$,连接$PD'$,如图②,由题干可知$∠PAD=∠D'$,$\because ∠C=∠D'$,$\therefore ∠PAD=∠PCA$.又$\because ∠C+∠CPA+∠CAP=180^{\circ}$,$∠PAD+∠PAC+∠CAB=180^{\circ}$,$\therefore ∠CAB=∠CPA$.

知识运用:如图③,连接$DF$,$\because AD$是$\triangle ABC$中$∠BAC$的平分线,$\therefore ∠BAD=∠CAD$.$\because$ 经过点$A$的$\odot O$与$BC$相切于点$D$,$\therefore ∠CDF=∠CAD$,$\therefore ∠BAD=∠CDF$.$\because ∠BAD=∠DFE$,$\therefore ∠CDF=∠DFE$,$\therefore EF// BC$.
归纳总结
(1)弦切角的定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
(2)弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
查看更多完整答案,请扫码查看


