第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
1. (2023·兰州中考改编)已知二次函数$y = - 3(x - 2)^2 - 3$,下列说法正确的是 (
A. 图象开口向上
B. 对称轴为直线$x = - 2$
C. 顶点坐标为$(2,3)$
D. 函数的最大值是$-3$
D
)A. 图象开口向上
B. 对称轴为直线$x = - 2$
C. 顶点坐标为$(2,3)$
D. 函数的最大值是$-3$
答案:
D
2. (益阳中考改编)若抛物线$y = (x - m)^2 + 1 - m$的顶点在第一象限,则$m$的取值范围是 (
A. $m > 0$
B. $m > 1$
C. $- 1 < m < 0$
D. $0 < m < 1$
D
)A. $m > 0$
B. $m > 1$
C. $- 1 < m < 0$
D. $0 < m < 1$
答案:
D
3. (温州中考)已知点$A(a,2)$,$B(b,2)$,$C(c,7)都在抛物线y = (x - 1)^2 - 2$上,点$A在点B$左侧,下列选项正确的是 (
A. 若$c < 0$,则$a < c < b$
B. 若$c < 0$,则$a < b < c$
C. 若$c > 0$,则$a < c < b$
D. 若$c > 0$,则$a < b < c$
D
)A. 若$c < 0$,则$a < c < b$
B. 若$c < 0$,则$a < b < c$
C. 若$c > 0$,则$a < c < b$
D. 若$c > 0$,则$a < b < c$
答案:
D
4. 原创题 补全表格。
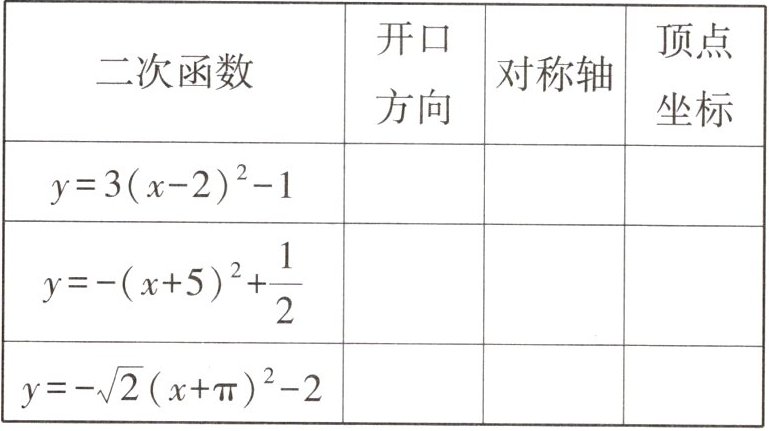
(注:因无法直接查看图片中的答题空位置,根据常见表格补全形式,推测答案对应位置如下:开口方向依次为

(注:因无法直接查看图片中的答题空位置,根据常见表格补全形式,推测答案对应位置如下:开口方向依次为
向上
、向下
、向下
;对称轴依次为x=2
、x=−5
、x=−π
;顶点坐标依次为(2,−1)
、(−5,$\frac{1}{2}$)
、(−π,−2)
)
答案:
向上 x=2 (2,−1) 向下 x=−5 (−5,$\frac{1}{2}$) 向下 x=−π (−π,−2)
5. (1)(2023·广西中考改编)将抛物线$y = x^2$先向右平移3个单位长度,再向上平移4个单位长度,得到的抛物线是
(2)(2023·牡丹江中考)将抛物线$y = (x + 3)^2$向下平移1个单位长度,再向右平移
y=(x−3)²+4
。(2)(2023·牡丹江中考)将抛物线$y = (x + 3)^2$向下平移1个单位长度,再向右平移
2或4
个单位长度后,得到的新抛物线经过原点。
答案:
(1)y=(x−3)²+4
(2)2或4
(1)y=(x−3)²+4
(2)2或4
6. (1)二次函数$y = 2(x + 1)^2 + 3的图象上有三个不同的点A(x_1,m)$,$B(x_1 + x_2,n)$,$C(x_2,m)$,则$n$的值为
(2)(宁波中考)点$A(m - 1,y_1)$,$B(m,y_2)都在二次函数y = (x - 1)^2 + n$的图象上。若$y_1 < y_2$,则$m$的取值范围为
5
。(2)(宁波中考)点$A(m - 1,y_1)$,$B(m,y_2)都在二次函数y = (x - 1)^2 + n$的图象上。若$y_1 < y_2$,则$m$的取值范围为
m>$\frac{3}{2}$
。
答案:
(1)5
(2)m>$\frac{3}{2}$
(1)5
(2)m>$\frac{3}{2}$
7. 改编题 将抛物线$y_1 = a(x - h)^2 + k$先向左平移2个单位长度,再向上平移3个单位长度得到抛物线$y_2 = - 2(x + 3)^2 + 1$。
(1)$a = $
(2)当$- 2 < x < 2$时,求$y_1$和$y_2$的取值范围;
(3)若抛物线$y_1$不动,而把$x$轴向下平移2个单位长度,$y$轴向右平移3个单位长度,在新坐标系下得到抛物线$y_3$,求$y_3$的解析式。
(1)$a = $
−2
,$h = $−1
,$k = $−2
;(2)当$- 2 < x < 2$时,求$y_1$和$y_2$的取值范围;
−20<y₁≤−2,−49<y₂<−1.
(3)若抛物线$y_1$不动,而把$x$轴向下平移2个单位长度,$y$轴向右平移3个单位长度,在新坐标系下得到抛物线$y_3$,求$y_3$的解析式。
$y_3=-2(x + 4)^2$
答案:
(1)−2 −1 −2
(2)−20<y₁≤−2,−49<y₂<−1.
(3)y₁=−2(x + 1)²−2的顶点坐标为(−1,−2),若把x轴向下平移2个单位长度,y轴向右平移3个单位长度,则在新坐标系中抛物线的顶点坐标为(−4,0),
∴抛物线y₃的解析式为y₃=−2(x + 4)².
归纳总结
①抛物线不动,把x轴向下(上)平移n个单位长度,相当于坐标轴不动,把抛物线向上(下)平移n个单位长度;
②抛物线不动,把y轴向左(右)平移n个单位长度,相当于坐标轴不动,把抛物线向右(左)平移n个单位长度.
(1)−2 −1 −2
(2)−20<y₁≤−2,−49<y₂<−1.
(3)y₁=−2(x + 1)²−2的顶点坐标为(−1,−2),若把x轴向下平移2个单位长度,y轴向右平移3个单位长度,则在新坐标系中抛物线的顶点坐标为(−4,0),
∴抛物线y₃的解析式为y₃=−2(x + 4)².
归纳总结
①抛物线不动,把x轴向下(上)平移n个单位长度,相当于坐标轴不动,把抛物线向上(下)平移n个单位长度;
②抛物线不动,把y轴向左(右)平移n个单位长度,相当于坐标轴不动,把抛物线向右(左)平移n个单位长度.
8. (衢州中考)已知二次函数$y = a(x - 1)^2 - a(a \neq 0)$,当$- 1 \leq x \leq 4$时,$y的最小值为- 4$,则$a$的值为 (
A. $\frac{1}{2}$或4
B. $\frac{4}{3}或- \frac{1}{2}$
C. $- \frac{4}{3}$或4
D. $- \frac{1}{2}$或4
D
)A. $\frac{1}{2}$或4
B. $\frac{4}{3}或- \frac{1}{2}$
C. $- \frac{4}{3}$或4
D. $- \frac{1}{2}$或4
答案:
D
9. 如图,点A(m,5),B(n,2)是抛物线$C_1:y = \frac{1}{2}(x -$$2)^2 + 1$上的两点,将该抛物线向左平移,得到抛物线$C_2:y = \frac{1}{2}(x + 1)^2 + 1,$点A,B的对应点分别为点A',B',则曲线段AB扫过的阴影部分面积为 (
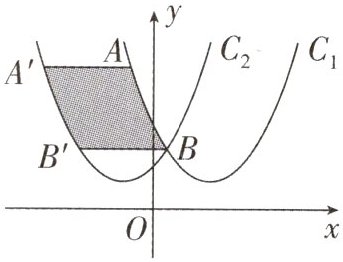
A. 6
B. 9
C. 12
D. 15
B
)
A. 6
B. 9
C. 12
D. 15
答案:
B
查看更多完整答案,请扫码查看


