第122页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
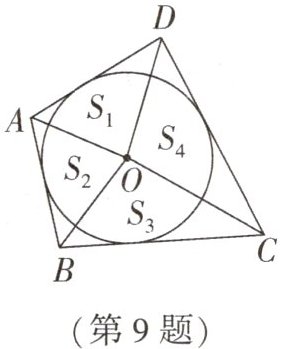
9.如图,$\odot O$内切于四边形ABCD.
(1)若$AB= 6,BC= 9,CD= 11$,则AD的长度为____
(2)若连接AO,BO,CO,DO,记$\triangle AOD,\triangle AOB,$$\triangle COB,\triangle DOC的面积分别为S_{1},S_{2},S_{3},S_{4},则S_{1},S_{2},S_{3},S_{4}$的数量关系为____
(1)若$AB= 6,BC= 9,CD= 11$,则AD的长度为____
8
____;(2)若连接AO,BO,CO,DO,记$\triangle AOD,\triangle AOB,$$\triangle COB,\triangle DOC的面积分别为S_{1},S_{2},S_{3},S_{4},则S_{1},S_{2},S_{3},S_{4}$的数量关系为____
S₁ + S₃ = S₂ + S₄
____.
答案:
(1)8
(2)S₁ + S₃ = S₂ + S₄
(1)8
(2)S₁ + S₃ = S₂ + S₄
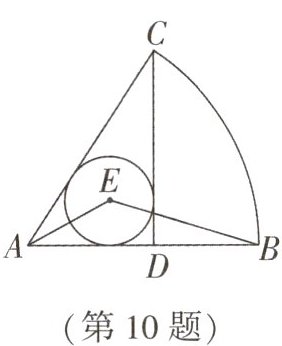
10.(威海中考)如图,在扇形CAB中,$CD⊥AB,$垂足为点D,$\odot E是\triangle ACD$的内切圆,连接AE,BE,则$∠AEB$的度数为
135°
.
答案:
135°
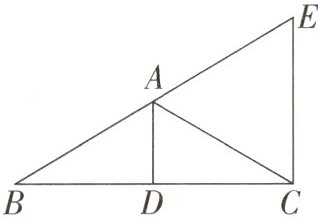
11.(长沙中考)如图,在$\triangle ABC$中,AD是边BC上的中线,$∠BAD= ∠CAD,CE// AD$,CE交BA的延长线于点E,$BC= 8,AD= 3.$
(1)求CE的长;
(2)求证:$\triangle ABC$为等腰三角形;
(3)求$\triangle ABC$的外接圆圆心P与内切圆圆心Q之间的距离.
(1)求CE的长;
(2)求证:$\triangle ABC$为等腰三角形;
(3)求$\triangle ABC$的外接圆圆心P与内切圆圆心Q之间的距离.

答案:
(1)
∵AD是边BC上的中线,
∴BD = CD。
∵CE//AD,
∴AD为△BCE的中位线,
∴CE = 2AD = 6。
(2)
∵CE//AD,
∴∠BAD = ∠E,∠CAD = ∠ACE。而∠BAD = ∠CAD,
∴∠ACE = ∠E,
∴AE = AC;而AB = AE,
∴AB = AC,
∴△ABC为等腰三角形。
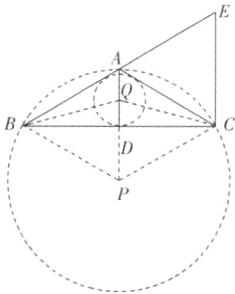
(3)如图,连接BP,BQ,CP,CQ,在Rt△ABD中,AB = $\sqrt{3^{2}+4^{2}} = 5$,设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中,(R - 3)² + 4² = R²,解得R = $\frac{25}{6}$,
∴PD = PA - AD = $\frac{25}{6}-3=\frac{7}{6}$。
∵S△ABQ + S△BCQ + S△ACQ = S△ABC,
∴$\frac{1}{2}$·r·5 + $\frac{1}{2}$·r·8 + $\frac{1}{2}$·r·5 = $\frac{1}{2}$×3×8,解得r = $\frac{4}{3}$,即QD = $\frac{4}{3}$,
∴PQ = PD + QD = $\frac{7}{6}+\frac{4}{3}=\frac{5}{2}$。故△ABC的外接圆圆心P与内切圆圆心Q之间的距离为$\frac{5}{2}$。
知识拓展
任意三角形的外接圆半径R、内切圆半径r,O和I分别为其外心和内心:r² + OI² = (R - r)²或OI² = R² - 2Rr。
(1)
∵AD是边BC上的中线,
∴BD = CD。
∵CE//AD,
∴AD为△BCE的中位线,
∴CE = 2AD = 6。
(2)
∵CE//AD,
∴∠BAD = ∠E,∠CAD = ∠ACE。而∠BAD = ∠CAD,
∴∠ACE = ∠E,
∴AE = AC;而AB = AE,
∴AB = AC,
∴△ABC为等腰三角形。
(3)如图,连接BP,BQ,CP,CQ,在Rt△ABD中,AB = $\sqrt{3^{2}+4^{2}} = 5$,设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中,(R - 3)² + 4² = R²,解得R = $\frac{25}{6}$,
∴PD = PA - AD = $\frac{25}{6}-3=\frac{7}{6}$。
∵S△ABQ + S△BCQ + S△ACQ = S△ABC,
∴$\frac{1}{2}$·r·5 + $\frac{1}{2}$·r·8 + $\frac{1}{2}$·r·5 = $\frac{1}{2}$×3×8,解得r = $\frac{4}{3}$,即QD = $\frac{4}{3}$,
∴PQ = PD + QD = $\frac{7}{6}+\frac{4}{3}=\frac{5}{2}$。故△ABC的外接圆圆心P与内切圆圆心Q之间的距离为$\frac{5}{2}$。

知识拓展
任意三角形的外接圆半径R、内切圆半径r,O和I分别为其外心和内心:r² + OI² = (R - r)²或OI² = R² - 2Rr。
12.在关于x的方程$x^{2}-2ax+\frac {1}{4}b^{2}= 0$中,a,b分别是一个面积为12的等腰三角形的腰与底边的长,且这个方程的两根之差的绝对值为8,则这个三角形的内切圆面积是____.
答案:
$\frac{9\pi}{4}$ 解析:如图,AB = AC = a,BC = b,AE⊥BC于点E,FD⊥AB于点D,⊙F是△ABC的内切圆,
∴BE = $\frac{1}{2}$BC = $\frac{1}{2}$b,AE = $\sqrt{AB^{2}-BE^{2}}=\frac{1}{2}\sqrt{4a^{2}-b^{2}}$。设方程x² - 2ax + $\frac{1}{4}$b² = 0的两根分别为x₁,x₂,
∴x₁ + x₂ = 2a,x₁x₂ = $\frac{1}{4}$b²。又|x₁ - x₂| = 8,
∴(x₁ + x₂)² - 4x₁x₂ = 64,即4a² - b² = 64。又S△ABC = $\frac{1}{2}$×b×$\frac{1}{2}\sqrt{4a^{2}-b^{2}}$ = 12,与4a² - b² = 64联立方程组,解得b = 6,a = 5。设内切圆半径为r,则EF = DF = r,
∴BE = BD = 3,AD = AB - BD = 2,AD² + DF² = AF² = (AE - EF)²,
∴2² + r² = (4 - r)²,解得r = $\frac{3}{2}$,
∴三角形的内切圆面积为π×($\frac{3}{2}$)² = $\frac{9\pi}{4}$。

$\frac{9\pi}{4}$ 解析:如图,AB = AC = a,BC = b,AE⊥BC于点E,FD⊥AB于点D,⊙F是△ABC的内切圆,
∴BE = $\frac{1}{2}$BC = $\frac{1}{2}$b,AE = $\sqrt{AB^{2}-BE^{2}}=\frac{1}{2}\sqrt{4a^{2}-b^{2}}$。设方程x² - 2ax + $\frac{1}{4}$b² = 0的两根分别为x₁,x₂,
∴x₁ + x₂ = 2a,x₁x₂ = $\frac{1}{4}$b²。又|x₁ - x₂| = 8,
∴(x₁ + x₂)² - 4x₁x₂ = 64,即4a² - b² = 64。又S△ABC = $\frac{1}{2}$×b×$\frac{1}{2}\sqrt{4a^{2}-b^{2}}$ = 12,与4a² - b² = 64联立方程组,解得b = 6,a = 5。设内切圆半径为r,则EF = DF = r,
∴BE = BD = 3,AD = AB - BD = 2,AD² + DF² = AF² = (AE - EF)²,
∴2² + r² = (4 - r)²,解得r = $\frac{3}{2}$,
∴三角形的内切圆面积为π×($\frac{3}{2}$)² = $\frac{9\pi}{4}$。

13.使用“面积法”解决下列问题:
(1)$Rt\triangle ABC$两条直角边长分别为3和4,则它的内切圆半径为____;
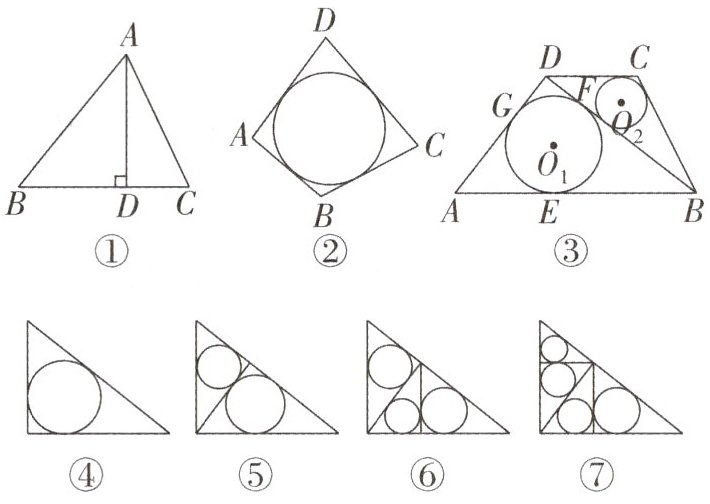
(2)如图①,在$\triangle ABC$中,$AB= 15,BC= 14,$$AC= 13$,AD是BC边上的高,求AD长及$\triangle ABC$的内切圆的半径;
(3)若$\triangle ABC$的周长为l,面积为S,内切圆$\odot O$的半径为r,直接写出r与S,l之间的关系:____;
(4)若四边形ABCD存在内切圆(与各边都相切的圆),如图②,且四边形ABCD的面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(5)如图③,在四边形ABCD中,$\odot O_{1}与\odot O_{2}分别为\triangle ABD与\triangle BCD$的内切圆,$\odot O_{1}与\triangle ABD$分别相切于点E,F,G,设它们的半径分别为$r_{1}和r_{2}$,若$∠ADB= 90^{\circ },AE= $$8,BC+CD= 20,S_{\triangle DBC}= 36,r_{2}= 2$,求$r_{1}$的值;
(6)如图④~⑦,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,图⑬中有10个直角三角形的内切圆,它们的面积分别记为$S_{1},S_{2},S_{3},... ,S_{10}$,则$S_{1}+S_{2}+S_{3}+... +$$S_{10}= $____.
(1)$Rt\triangle ABC$两条直角边长分别为3和4,则它的内切圆半径为____;
(2)如图①,在$\triangle ABC$中,$AB= 15,BC= 14,$$AC= 13$,AD是BC边上的高,求AD长及$\triangle ABC$的内切圆的半径;
(3)若$\triangle ABC$的周长为l,面积为S,内切圆$\odot O$的半径为r,直接写出r与S,l之间的关系:____;
(4)若四边形ABCD存在内切圆(与各边都相切的圆),如图②,且四边形ABCD的面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(5)如图③,在四边形ABCD中,$\odot O_{1}与\odot O_{2}分别为\triangle ABD与\triangle BCD$的内切圆,$\odot O_{1}与\triangle ABD$分别相切于点E,F,G,设它们的半径分别为$r_{1}和r_{2}$,若$∠ADB= 90^{\circ },AE= $$8,BC+CD= 20,S_{\triangle DBC}= 36,r_{2}= 2$,求$r_{1}$的值;
(6)如图④~⑦,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,图⑬中有10个直角三角形的内切圆,它们的面积分别记为$S_{1},S_{2},S_{3},... ,S_{10}$,则$S_{1}+S_{2}+S_{3}+... +$$S_{10}= $____.

答案:
(1)1
(2)设BD = x,则CD = 14 - x,设△ABC的内切圆的半径为r,由勾股定理可得AD² = AB² - BD² = 15² - x²,AD² = AC² - CD² = 13² - (14 - x)²,则15² - x² = 13² - (14 - x)²,解得x = 9,则AD = 12,
∴$\frac{1}{2}$BC·AD = $\frac{1}{2}$(AB + BC + AC)·r,
∴r = $\frac{14×12}{15 + 14 + 13}$ = 4。
(3)r = $\frac{2S}{l}$
(4)设四边形ABCD内切圆的圆心为O,半径为r,连接OA,OB,OC,OD,则S = S△OAB + S△OBC + S△OCD + S△OAD = $\frac{1}{2}$AB·r + $\frac{1}{2}$BC·r + $\frac{1}{2}$CD·r + $\frac{1}{2}$DA·r = $\frac{1}{2}$(a + b + c + d)·r,
∴r = $\frac{2S}{a + b + c + d}$。
(5)
∵S△DBC = 36,r₂ = 2,
∴BC + CD + BD = $\frac{2S_{\triangle DBC}}{r_{2}}$ = 36。
∵BC + CD = 20,
∴BD = 16。
∵⊙O₁是△ABD的内切圆,
∴AE = AG = 8,BE = BF,DF = DG,
∴DG + BE = BD = 16,
∴设DG = x,则BE = 16 - x。
∵∠ADB = 90°,
∴AD² + BD² = AB²,即(8 + x)² + 16² = (8 + 16 - x)²,解得x = 4,
∴AD = AG + DG = 8 + 4 = 12,
∴S△ABD = $\frac{1}{2}$AD·BD = $\frac{1}{2}$×12×16 = 96。
∵AD + AB + BD = AG + AE + (DG + BE) + BD = 8 + 8 + 16 + 16 = 48,
∴r₁ = $\frac{2S_{\triangle ABD}}{AD + AB + BD}$ = $\frac{96×2}{48}$ = 4。
(6)π 解析:如图①,分别过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,易得四边形OECF为矩形。
∵OE = OF,
∴矩形OECF为正方形。设圆O的半径为r,则OE = OF = r = $\frac{3 + 4 - 5}{2}$ = 1,
∴S₁ = π×1² = π。如图②,由S△ABC = $\frac{1}{2}$×3×4 = $\frac{1}{2}$×5×CD,得CD = $\frac{12}{5}$。由勾股定理得AD = $\frac{9}{5}$,BD = 5 - $\frac{9}{5}$ = $\frac{16}{5}$。由上可知⊙O的半径为$\frac{\frac{9}{5}+\frac{12}{5}-3}{2}=\frac{3}{5}$,⊙E的半径为$\frac{\frac{12}{5}+\frac{16}{5}-4}{2}=\frac{4}{5}$,
∴S₁ + S₂ = π×($\frac{3}{5}$)² + π×($\frac{4}{5}$)² = π。如图③,由S△CDB = $\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$ = $\frac{1}{2}$×4×MD,得MD = $\frac{48}{25}$。由勾股定理得CM = $\frac{36}{25}$,MB = 4 - $\frac{36}{25}$ = $\frac{64}{25}$,由上可知⊙O的半径为$\frac{3}{5}$,⊙E的半径为$\frac{12}{25}$,⊙F的半径为$\frac{16}{25}$,
∴S₁ + S₂ + S₃ = π×($\frac{3}{5}$)² + π×($\frac{12}{25}$)² + π×($\frac{16}{25}$)² = π,…,以此类推,可得S₁ + S₂ + S₃ + … + Sₙ = π,
∴S₁ + S₂ + S₃ + … + S₁₀ = π。

归纳总结
已知任意△ABC的三边为a,b,c,三角形外接圆半径R = $\frac{abc}{4S}$,内切圆半径r = $\frac{2S}{a + b + c}$。(S为△ABC的面积,同一三角形的外接圆和内切圆半径满足关系式:2Rr = $\frac{abc}{a + b + c}$)
(1)1
(2)设BD = x,则CD = 14 - x,设△ABC的内切圆的半径为r,由勾股定理可得AD² = AB² - BD² = 15² - x²,AD² = AC² - CD² = 13² - (14 - x)²,则15² - x² = 13² - (14 - x)²,解得x = 9,则AD = 12,
∴$\frac{1}{2}$BC·AD = $\frac{1}{2}$(AB + BC + AC)·r,
∴r = $\frac{14×12}{15 + 14 + 13}$ = 4。
(3)r = $\frac{2S}{l}$
(4)设四边形ABCD内切圆的圆心为O,半径为r,连接OA,OB,OC,OD,则S = S△OAB + S△OBC + S△OCD + S△OAD = $\frac{1}{2}$AB·r + $\frac{1}{2}$BC·r + $\frac{1}{2}$CD·r + $\frac{1}{2}$DA·r = $\frac{1}{2}$(a + b + c + d)·r,
∴r = $\frac{2S}{a + b + c + d}$。
(5)
∵S△DBC = 36,r₂ = 2,
∴BC + CD + BD = $\frac{2S_{\triangle DBC}}{r_{2}}$ = 36。
∵BC + CD = 20,
∴BD = 16。
∵⊙O₁是△ABD的内切圆,
∴AE = AG = 8,BE = BF,DF = DG,
∴DG + BE = BD = 16,
∴设DG = x,则BE = 16 - x。
∵∠ADB = 90°,
∴AD² + BD² = AB²,即(8 + x)² + 16² = (8 + 16 - x)²,解得x = 4,
∴AD = AG + DG = 8 + 4 = 12,
∴S△ABD = $\frac{1}{2}$AD·BD = $\frac{1}{2}$×12×16 = 96。
∵AD + AB + BD = AG + AE + (DG + BE) + BD = 8 + 8 + 16 + 16 = 48,
∴r₁ = $\frac{2S_{\triangle ABD}}{AD + AB + BD}$ = $\frac{96×2}{48}$ = 4。
(6)π 解析:如图①,分别过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,易得四边形OECF为矩形。
∵OE = OF,
∴矩形OECF为正方形。设圆O的半径为r,则OE = OF = r = $\frac{3 + 4 - 5}{2}$ = 1,
∴S₁ = π×1² = π。如图②,由S△ABC = $\frac{1}{2}$×3×4 = $\frac{1}{2}$×5×CD,得CD = $\frac{12}{5}$。由勾股定理得AD = $\frac{9}{5}$,BD = 5 - $\frac{9}{5}$ = $\frac{16}{5}$。由上可知⊙O的半径为$\frac{\frac{9}{5}+\frac{12}{5}-3}{2}=\frac{3}{5}$,⊙E的半径为$\frac{\frac{12}{5}+\frac{16}{5}-4}{2}=\frac{4}{5}$,
∴S₁ + S₂ = π×($\frac{3}{5}$)² + π×($\frac{4}{5}$)² = π。如图③,由S△CDB = $\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$ = $\frac{1}{2}$×4×MD,得MD = $\frac{48}{25}$。由勾股定理得CM = $\frac{36}{25}$,MB = 4 - $\frac{36}{25}$ = $\frac{64}{25}$,由上可知⊙O的半径为$\frac{3}{5}$,⊙E的半径为$\frac{12}{25}$,⊙F的半径为$\frac{16}{25}$,
∴S₁ + S₂ + S₃ = π×($\frac{3}{5}$)² + π×($\frac{12}{25}$)² + π×($\frac{16}{25}$)² = π,…,以此类推,可得S₁ + S₂ + S₃ + … + Sₙ = π,
∴S₁ + S₂ + S₃ + … + S₁₀ = π。

归纳总结
已知任意△ABC的三边为a,b,c,三角形外接圆半径R = $\frac{abc}{4S}$,内切圆半径r = $\frac{2S}{a + b + c}$。(S为△ABC的面积,同一三角形的外接圆和内切圆半径满足关系式:2Rr = $\frac{abc}{a + b + c}$)
查看更多完整答案,请扫码查看


