第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
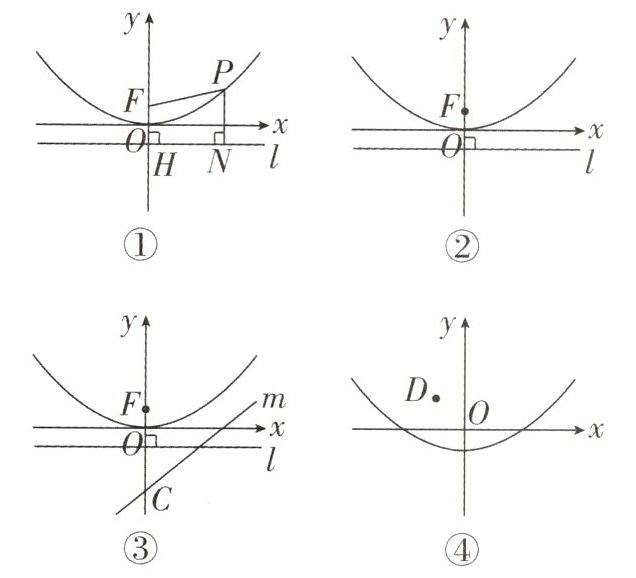
1. (2023·鄂州中考)某数学兴趣小组运用《几何画板》软件探究$y = ax^{2}(a > 0)$型抛物线图象.发现:如图①所示,该类型图象上任意一点$P到定点F(0,\frac{1}{4a})的距离PF$,始终等于它到定直线$l:y = -\frac{1}{4a}的距离PN$(该结论不需要证明).他们称:定点$F$为图象的焦点,定直线$l$为图象的准线,$y = -\frac{1}{4a}$叫做抛物线的准线方程.准线$l与y轴的交点为H$.其中原点$O为FH$的中点,$FH = 2OF = \frac{1}{2a}$.
【基础训练】(1)请分别直接写出抛物线$y = \frac{1}{4}x^{2}的焦点坐标和准线l$的方程:____,____.
【技能训练】(2)如图②,已知抛物线$y = \frac{1}{4}x^{2}上一点P(x_{0},y_{0})(x_{0} > 0)到焦点F的距离是它到x轴距离的3$倍,求点$P$的坐标.
【能力提升】(3)如图③,已知抛物线$y = \frac{1}{4}x^{2}的焦点为F$,准线方程为$l$.直线$m:y = \frac{1}{2}x - 3交y轴于点C$,抛物线上动点$P到x轴的距离为d_{1}$,到直线$m的距离为d_{2}$,请直接写出$d_{1} + d_{2}$的最小值.
【拓展延伸】该兴趣小组继续探究还发现:若将抛物线$y = ax^{2}(a > 0)平移至y = a(x - h)^{2} + k(a > 0)$.抛物线$y = a(x - h)^{2} + k(a > 0)内有一定点F(h,k + \frac{1}{4a})$,直线$l过点M(h,k - \frac{1}{4a})且与x$轴平行.当动点$P$在该抛物线上运动时,点$P到直线l的距离PP_{1}始终等于点P到点F$的距离(该结论不需要证明).
请阅读上面的材料,探究下题:
(4)如图④,点$D(-1,\frac{3}{2})$是第二象限内一定点,点$P是抛物线y = \frac{1}{4}x^{2} - 1$上一动点,当$PO + PD$取最小值时,请求出$\triangle POD$的面积.
【基础训练】(1)请分别直接写出抛物线$y = \frac{1}{4}x^{2}的焦点坐标和准线l$的方程:____,____.
【技能训练】(2)如图②,已知抛物线$y = \frac{1}{4}x^{2}上一点P(x_{0},y_{0})(x_{0} > 0)到焦点F的距离是它到x轴距离的3$倍,求点$P$的坐标.
【能力提升】(3)如图③,已知抛物线$y = \frac{1}{4}x^{2}的焦点为F$,准线方程为$l$.直线$m:y = \frac{1}{2}x - 3交y轴于点C$,抛物线上动点$P到x轴的距离为d_{1}$,到直线$m的距离为d_{2}$,请直接写出$d_{1} + d_{2}$的最小值.
【拓展延伸】该兴趣小组继续探究还发现:若将抛物线$y = ax^{2}(a > 0)平移至y = a(x - h)^{2} + k(a > 0)$.抛物线$y = a(x - h)^{2} + k(a > 0)内有一定点F(h,k + \frac{1}{4a})$,直线$l过点M(h,k - \frac{1}{4a})且与x$轴平行.当动点$P$在该抛物线上运动时,点$P到直线l的距离PP_{1}始终等于点P到点F$的距离(该结论不需要证明).
请阅读上面的材料,探究下题:
(4)如图④,点$D(-1,\frac{3}{2})$是第二象限内一定点,点$P是抛物线y = \frac{1}{4}x^{2} - 1$上一动点,当$PO + PD$取最小值时,请求出$\triangle POD$的面积.

答案:
(1) $(0,1)$ $y = -1$
(2) 由
(1)知抛物线 $y=\frac{1}{4}x^{2}$ 的焦点 $F$ 的坐标为 $(0,1)$。$\because$ 点 $P(x_{0},y_{0})(x_{0}>0)$ 到焦点 $F$ 的距离是它到 $x$ 轴距离的 $3$ 倍,$\therefore\sqrt{x_{0}^{2}+(y_{0}-1)^{2}} = 3y_{0}$,整理得 $x_{0}^{2}=8y_{0}^{2}+2y_{0}-1$。又 $\because y_{0}=\frac{1}{4}x_{0}^{2}$,$\therefore4y_{0}=8y_{0}^{2}+2y_{0}-1$,解得 $y_{0}=\frac{1}{2}$ 或 $y_{0}=-\frac{1}{4}$(舍去),$\therefore x_{0}=\sqrt{2}$,$\therefore$ 点 $P$ 的坐标为 $(\sqrt{2},\frac{1}{2})$。
(3) $d_{1}+d_{2}$ 的最小值为 $\frac{8\sqrt{5}}{5}-1$。解析:过点 $P$ 作 $PE\perp$ 直线 $m$ 于点 $E$,过点 $P$ 作 $PG\perp$ 准线 $l$ 于点 $G$,结合题意和
(1)中结论可知 $PG = PF = d_{1}+1$,$PE = d_{2}$,如图①。
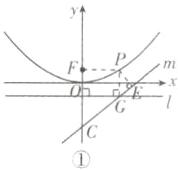
若使得 $d_{1}+d_{2}$ 取最小值,即 $PF + PE - 1$ 的值最小,需 $F$,$P$,$E$ 三点共线,此时 $PF + PE - 1 = EF - 1$,即此时 $d_{1}+d_{2}$ 的值最小。$\because$ 直线 $PE$ 与直线 $m$ 垂直,故设直线 $PE$ 的解析式为 $y = -2x + b$,将 $F(0,1)$ 代入,解得 $b = 1$,$\therefore$ 直线 $PE$ 的解析式为 $y = -2x + 1$。$\because$ 点 $E$ 是直线 $PE$ 和直线 $m$ 的交点,令 $-2x + 1=\frac{1}{2}x - 3$,解得 $x=\frac{8}{5}$,故点 $E$ 的坐标为 $(\frac{8}{5},-\frac{11}{5})$,$\therefore EF=\sqrt{(\frac{8}{5})^{2}+(-\frac{11}{5}-1)^{2}}=\frac{8\sqrt{5}}{5}$,$d_{1}+d_{2}=\frac{8\sqrt{5}}{5}-1$。即 $d_{1}+d_{2}$ 的最小值为 $\frac{8\sqrt{5}}{5}-1$。
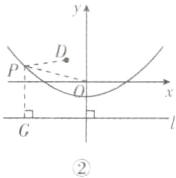
(4) $\because$ 抛物线 $y=\frac{1}{4}x^{2}-1$ 中 $a=\frac{1}{4}$,$\therefore\frac{1}{4a}=1$,$-\frac{1}{4a}=-1$,$\therefore$ 抛物线 $y=\frac{1}{4}x^{2}-1$ 的焦点坐标为 $F(0,0)$,准线 $l$ 的方程为 $y = -2$,过点 $P$ 作 $PG\perp$ 准线 $l$ 交于点 $G$,结合题意和[拓展延伸]中结论可知 $PG = PO$,则 $PO + PD = PG + PD$,如图②。
若使得 $PO + PD$ 取最小值,即 $PG + PD$ 的值最小,故当 $D$,$P$,$G$ 三点共线时,$PO + PD = PG + PD = DG$,即此刻 $PO + PD$ 的值最小,如图③。

$\because$ 点 $D$ 的坐标为 $(-1,\frac{3}{2})$,$DG\perp$ 准线 $l$,$\therefore$ 点 $P$ 的横坐标为 $-1$,代入 $y=\frac{1}{4}x^{2}-1$,解得 $y = -\frac{3}{4}$,即 $P(-1,-\frac{3}{4})$,$DP=\frac{3}{2}+\frac{3}{4}=\frac{9}{4}$,则 $\triangle POD$ 的面积为 $\frac{1}{2}\times\frac{9}{4}\times1=\frac{9}{8}$。
(1) $(0,1)$ $y = -1$
(2) 由
(1)知抛物线 $y=\frac{1}{4}x^{2}$ 的焦点 $F$ 的坐标为 $(0,1)$。$\because$ 点 $P(x_{0},y_{0})(x_{0}>0)$ 到焦点 $F$ 的距离是它到 $x$ 轴距离的 $3$ 倍,$\therefore\sqrt{x_{0}^{2}+(y_{0}-1)^{2}} = 3y_{0}$,整理得 $x_{0}^{2}=8y_{0}^{2}+2y_{0}-1$。又 $\because y_{0}=\frac{1}{4}x_{0}^{2}$,$\therefore4y_{0}=8y_{0}^{2}+2y_{0}-1$,解得 $y_{0}=\frac{1}{2}$ 或 $y_{0}=-\frac{1}{4}$(舍去),$\therefore x_{0}=\sqrt{2}$,$\therefore$ 点 $P$ 的坐标为 $(\sqrt{2},\frac{1}{2})$。
(3) $d_{1}+d_{2}$ 的最小值为 $\frac{8\sqrt{5}}{5}-1$。解析:过点 $P$ 作 $PE\perp$ 直线 $m$ 于点 $E$,过点 $P$ 作 $PG\perp$ 准线 $l$ 于点 $G$,结合题意和
(1)中结论可知 $PG = PF = d_{1}+1$,$PE = d_{2}$,如图①。


若使得 $d_{1}+d_{2}$ 取最小值,即 $PF + PE - 1$ 的值最小,需 $F$,$P$,$E$ 三点共线,此时 $PF + PE - 1 = EF - 1$,即此时 $d_{1}+d_{2}$ 的值最小。$\because$ 直线 $PE$ 与直线 $m$ 垂直,故设直线 $PE$ 的解析式为 $y = -2x + b$,将 $F(0,1)$ 代入,解得 $b = 1$,$\therefore$ 直线 $PE$ 的解析式为 $y = -2x + 1$。$\because$ 点 $E$ 是直线 $PE$ 和直线 $m$ 的交点,令 $-2x + 1=\frac{1}{2}x - 3$,解得 $x=\frac{8}{5}$,故点 $E$ 的坐标为 $(\frac{8}{5},-\frac{11}{5})$,$\therefore EF=\sqrt{(\frac{8}{5})^{2}+(-\frac{11}{5}-1)^{2}}=\frac{8\sqrt{5}}{5}$,$d_{1}+d_{2}=\frac{8\sqrt{5}}{5}-1$。即 $d_{1}+d_{2}$ 的最小值为 $\frac{8\sqrt{5}}{5}-1$。
(4) $\because$ 抛物线 $y=\frac{1}{4}x^{2}-1$ 中 $a=\frac{1}{4}$,$\therefore\frac{1}{4a}=1$,$-\frac{1}{4a}=-1$,$\therefore$ 抛物线 $y=\frac{1}{4}x^{2}-1$ 的焦点坐标为 $F(0,0)$,准线 $l$ 的方程为 $y = -2$,过点 $P$ 作 $PG\perp$ 准线 $l$ 交于点 $G$,结合题意和[拓展延伸]中结论可知 $PG = PO$,则 $PO + PD = PG + PD$,如图②。
若使得 $PO + PD$ 取最小值,即 $PG + PD$ 的值最小,故当 $D$,$P$,$G$ 三点共线时,$PO + PD = PG + PD = DG$,即此刻 $PO + PD$ 的值最小,如图③。

$\because$ 点 $D$ 的坐标为 $(-1,\frac{3}{2})$,$DG\perp$ 准线 $l$,$\therefore$ 点 $P$ 的横坐标为 $-1$,代入 $y=\frac{1}{4}x^{2}-1$,解得 $y = -\frac{3}{4}$,即 $P(-1,-\frac{3}{4})$,$DP=\frac{3}{2}+\frac{3}{4}=\frac{9}{4}$,则 $\triangle POD$ 的面积为 $\frac{1}{2}\times\frac{9}{4}\times1=\frac{9}{8}$。
2. (株洲中考改编)某学生在研究抛物线$y = ax^{2}(a < 0)$的性质时,将一直角三角板的直角顶点置于平面直角坐标系的原点$O$,两直角边与该抛物线交于$A,B$两点,请解答以下问题:
(1)若测得$OA = OB = 2\sqrt{2}$(如图①),求$a$的值;
(2)对同一条抛物线,该学生将三角板绕点$O$旋转到如图②所示位置时,过$B作BF \perp x轴于点F$,测得$OF = 1$,写出此时点$B$的坐标
(3)对该抛物线,该学生将三角板绕点$O$旋转任意角度时发现,交点$A,B$的连线段总经过一个固定的点,试说明理由,并求出该点的坐标
(1)若测得$OA = OB = 2\sqrt{2}$(如图①),求$a$的值;
$-\frac{1}{2}$
(2)对同一条抛物线,该学生将三角板绕点$O$旋转到如图②所示位置时,过$B作BF \perp x轴于点F$,测得$OF = 1$,写出此时点$B$的坐标
$(1,-\frac{1}{2})$
,并求点$A$的横坐标$-4$
;(3)对该抛物线,该学生将三角板绕点$O$旋转任意角度时发现,交点$A,B$的连线段总经过一个固定的点,试说明理由,并求出该点的坐标
$(0,-2)$
.
答案:
(1) 设线段 $AB$ 与 $y$ 轴的交点为 $C$,由抛物线的对称性可得 $C$ 为 $AB$ 的中点。$\because OA = OB = 2\sqrt{2}$,$\angle AOB = 90^{\circ}$,$\therefore AC = OC = BC = 2$,$\therefore B(2,-2)$。将 $B(2,-2)$ 代入抛物线 $y = ax^{2}(a<0)$,得 $a = -\frac{1}{2}$。
(2) 过点 $A$ 作 $AE\perp x$ 轴于点 $E$,$\because$ 点 $B$ 的横坐标为 $1$,$\therefore B(1,-\frac{1}{2})$。设 $A(-m,-\frac{1}{2}m^{2})(m>0)$,则 $OB^{2}=1^{2}+(-\frac{1}{2})^{2}=\frac{5}{4}$,$OA^{2}=m^{2}+\frac{1}{4}m^{4}$,$AB^{2}=(1 + m)^{2}+(-\frac{1}{2}+\frac{1}{2}m^{2})^{2}$。$\because\angle AOB = 90^{\circ}$,$\therefore AB^{2}=OA^{2}+OB^{2}$,$\therefore(1 + m)^{2}+(-\frac{1}{2}+\frac{1}{2}m^{2})^{2}=m^{2}+\frac{1}{4}m^{4}+\frac{5}{4}$,解得 $m_{1}=4$ 或 $m_{2}=0$(舍去),即点 $A$ 的横坐标为 $-4$。
(3) $\because$ 点 $A$,$B$ 是抛物线 $y = -\frac{1}{2}x^{2}$ 上的点,$\therefore$ 设 $A(-m,-\frac{1}{2}m^{2})(m>0)$,$B(n,-\frac{1}{2}n^{2})(n>0)$,设直线 $AB$ 的解析式为 $y = kx + b$,则 $\begin{cases}-mk + b = -\frac{1}{2}m^{2}\\nk + b = -\frac{1}{2}n^{2}\end{cases}$,解得 $b = -\frac{1}{2}mn$,故不论 $k$ 为何值,直线 $AB$ 恒过点 $(0,-\frac{1}{2}mn)$。而 $OA^{2}=m^{2}+\frac{1}{4}m^{4}$,$OB^{2}=n^{2}+\frac{1}{4}n^{4}$,$AB^{2}=(m + n)^{2}+(-\frac{1}{2}m^{2}+\frac{1}{2}n^{2})^{2}$,由 $OA^{2}+OB^{2}=AB^{2}$,得 $(m^{2}+\frac{1}{4}m^{4})+(n^{2}+\frac{1}{4}n^{4})=(m + n)^{2}+(-\frac{1}{2}m^{2}+\frac{1}{2}n^{2})^{2}$,解得 $mn = 4$,即 $b = -2$,故直线 $AB$ 恒过点 $(0,-2)$。
(1) 设线段 $AB$ 与 $y$ 轴的交点为 $C$,由抛物线的对称性可得 $C$ 为 $AB$ 的中点。$\because OA = OB = 2\sqrt{2}$,$\angle AOB = 90^{\circ}$,$\therefore AC = OC = BC = 2$,$\therefore B(2,-2)$。将 $B(2,-2)$ 代入抛物线 $y = ax^{2}(a<0)$,得 $a = -\frac{1}{2}$。
(2) 过点 $A$ 作 $AE\perp x$ 轴于点 $E$,$\because$ 点 $B$ 的横坐标为 $1$,$\therefore B(1,-\frac{1}{2})$。设 $A(-m,-\frac{1}{2}m^{2})(m>0)$,则 $OB^{2}=1^{2}+(-\frac{1}{2})^{2}=\frac{5}{4}$,$OA^{2}=m^{2}+\frac{1}{4}m^{4}$,$AB^{2}=(1 + m)^{2}+(-\frac{1}{2}+\frac{1}{2}m^{2})^{2}$。$\because\angle AOB = 90^{\circ}$,$\therefore AB^{2}=OA^{2}+OB^{2}$,$\therefore(1 + m)^{2}+(-\frac{1}{2}+\frac{1}{2}m^{2})^{2}=m^{2}+\frac{1}{4}m^{4}+\frac{5}{4}$,解得 $m_{1}=4$ 或 $m_{2}=0$(舍去),即点 $A$ 的横坐标为 $-4$。
(3) $\because$ 点 $A$,$B$ 是抛物线 $y = -\frac{1}{2}x^{2}$ 上的点,$\therefore$ 设 $A(-m,-\frac{1}{2}m^{2})(m>0)$,$B(n,-\frac{1}{2}n^{2})(n>0)$,设直线 $AB$ 的解析式为 $y = kx + b$,则 $\begin{cases}-mk + b = -\frac{1}{2}m^{2}\\nk + b = -\frac{1}{2}n^{2}\end{cases}$,解得 $b = -\frac{1}{2}mn$,故不论 $k$ 为何值,直线 $AB$ 恒过点 $(0,-\frac{1}{2}mn)$。而 $OA^{2}=m^{2}+\frac{1}{4}m^{4}$,$OB^{2}=n^{2}+\frac{1}{4}n^{4}$,$AB^{2}=(m + n)^{2}+(-\frac{1}{2}m^{2}+\frac{1}{2}n^{2})^{2}$,由 $OA^{2}+OB^{2}=AB^{2}$,得 $(m^{2}+\frac{1}{4}m^{4})+(n^{2}+\frac{1}{4}n^{4})=(m + n)^{2}+(-\frac{1}{2}m^{2}+\frac{1}{2}n^{2})^{2}$,解得 $mn = 4$,即 $b = -2$,故直线 $AB$ 恒过点 $(0,-2)$。
查看更多完整答案,请扫码查看


