第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
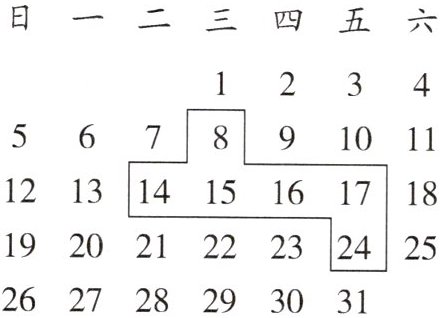
11.如图是某月的日历表,在此日历表上可以按图示形状圈出位置相邻的6个数(如:8,14,15,16,17,24).如果圈出的6个数中,最大数与最小数的积为225,则这6个数的和为
100
.
答案:
100
12.某种植物的根特别发达,它的主根长出若干数目的支根,支根中的$\frac{1}{3}$又长出同样多的小支根,而其余支根长出一半数目的小支根,主根、支根、小支根的总数是109个,则这种植物的主根长出
12
个支根.
答案:
12
13.在一次足球联赛中,组委会将若干支球队平均分成8小组,首先在小组中进行单循环赛(每两队赛一场),每组的前两名产生16强,然后在16强中进行淘汰赛(每两队淘汰一队),最后产生冠、亚、季军(季军的产生要多赛一场).组委会共需组织96场比赛(淘汰赛共16场),则一共有
40
支球队参赛.
答案:
40 解析:设每组有$x$支球队,则列方程为$\frac{8x(x - 1)}{2} + 16 = 96$,解得$x_1 = 5$,$x_2 = -4$(舍去),所以一共有$8×5 = 40$(支)球队参赛.
14.子曰:"吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩."
列方程解决问题:"大江东去浪淘尽,千古风流数周瑜,而立之年督东吴,早逝英年两位数,十位恰小个位三,个位平方与寿符,哪位学子算得快,多少年华数周瑜?"
列方程解决问题:"大江东去浪淘尽,千古风流数周瑜,而立之年督东吴,早逝英年两位数,十位恰小个位三,个位平方与寿符,哪位学子算得快,多少年华数周瑜?"
答案:
设周瑜逝世的年龄的个位数字为$x$,则十位数字为$x - 3$,根据题意得$10(x - 3) + x = x^2$,解得$x_1 = 5$,$x_2 = 6$,当$x_1 = 5$时,周瑜逝世的年龄是25岁.$\because$25岁小于而立之年,$\therefore$不符合题意,舍去.当$x_2 = 6$时,周瑜逝世的年龄是36岁,符合题意.故周瑜逝世的年龄是36岁.
15.新趋势项目式学习改编题握手问题探究:
【问题】(1)在一次聚会上,规定每两个人见面必须握1次手.若参加聚会的人数为6,则共握手
【变式】(2)①一个QQ群中有若干成员,每个成员都分别给群里其他成员发送了一条信息,这样共有756条信息,这个QQ群中共有
②小王毕业后选择去边疆支教,他的亲友为小王送行,小王及父母与前来送行的客人一一握手,客人之间也相互握手,但小王及父母之间不握手,共有88次握手,则送行的客人来了
【拓展】(3)①若一条直线上共有5个点,则这条直线上共有
②若一条线段AB上共有m个点(不含端点A,B),则共有线段
【应用】(4)一段铁路上共有6个火车站,若一列火车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备
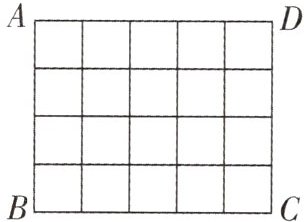
(5)已知由边长为1的小正方形拼成如图所示的矩形ABCD,图中共有
【问题】(1)在一次聚会上,规定每两个人见面必须握1次手.若参加聚会的人数为6,则共握手
15
次,若参加聚会的人数为n(n为正整数),则共握了$\frac{n(n - 1)}{2}$
次手.(用含n的代数式表示)【变式】(2)①一个QQ群中有若干成员,每个成员都分别给群里其他成员发送了一条信息,这样共有756条信息,这个QQ群中共有
28
个成员.②小王毕业后选择去边疆支教,他的亲友为小王送行,小王及父母与前来送行的客人一一握手,客人之间也相互握手,但小王及父母之间不握手,共有88次握手,则送行的客人来了
11
人.【拓展】(3)①若一条直线上共有5个点,则这条直线上共有
10
条线段.②若一条线段AB上共有m个点(不含端点A,B),则共有线段
$\frac{(m + 2)(m + 1)}{2}$
条.(用含m的代数式表示)【应用】(4)一段铁路上共有6个火车站,若一列火车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备
30
种不同的车票.(5)已知由边长为1的小正方形拼成如图所示的矩形ABCD,图中共有
150
个矩形,40
个正方形.
答案:
(1)15 $\frac{n(n - 1)}{2}$
(2)①28 ②11
(3)①10 ②$\frac{(m + 2)(m + 1)}{2}$
(4)30
(5)150 40 解析:题图中$AD$上有6个点,可得$AD$上有$\frac{6×5}{2} = 15$(条)线段;$AB$上有5个点,可得$AB$上有$\frac{5×4}{2} = 10$(条)线段.而$AD$上任意一条线段与$AB$上任意一条线段“握手”,都会构成一个矩形,$\therefore$图中共有$15×10 = 150$(个)矩形.$AD$上的线段与$AB$上的线段“握手”时,要构成正方形,就要求“握手”的两条线段必须相等.如表:
![img alt=15]
由表可得,共“握手”$20 + 12 + 6 + 2 = 40$(次),即题图中共有40个正方形.
归纳总结
“$C_n^2$模型”问题,即从$n$个元素中任选两个元素的组合数为$\frac{n(n - 1)}{2}$.如:两两握手问题、单循环比赛问题、若干点之间的线段数问题等.
(1)15 $\frac{n(n - 1)}{2}$
(2)①28 ②11
(3)①10 ②$\frac{(m + 2)(m + 1)}{2}$
(4)30
(5)150 40 解析:题图中$AD$上有6个点,可得$AD$上有$\frac{6×5}{2} = 15$(条)线段;$AB$上有5个点,可得$AB$上有$\frac{5×4}{2} = 10$(条)线段.而$AD$上任意一条线段与$AB$上任意一条线段“握手”,都会构成一个矩形,$\therefore$图中共有$15×10 = 150$(个)矩形.$AD$上的线段与$AB$上的线段“握手”时,要构成正方形,就要求“握手”的两条线段必须相等.如表:
![img alt=15]
由表可得,共“握手”$20 + 12 + 6 + 2 = 40$(次),即题图中共有40个正方形.
归纳总结
“$C_n^2$模型”问题,即从$n$个元素中任选两个元素的组合数为$\frac{n(n - 1)}{2}$.如:两两握手问题、单循环比赛问题、若干点之间的线段数问题等.
查看更多完整答案,请扫码查看


