第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
1. 教材 P83 练习 T2 变式 改编题 如图,半径为 2 的$\odot O$中,弦 AB 与弦 CD 垂直相交于点 P,连接 OP,若$OP= 1$,则$AB^{2}+CD^{2}$的值为 (
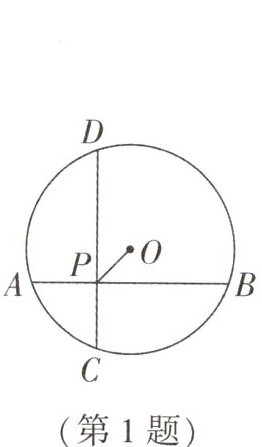
A. 16
B. 20
C. 24
D. 28
D
)
A. 16
B. 20
C. 24
D. 28
答案:
D
2. (荆州中考)如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高$AB= 20cm$,底面直径$BC= 12cm$,球的最高点到瓶底面的距离为 32 cm,则球的半径为______
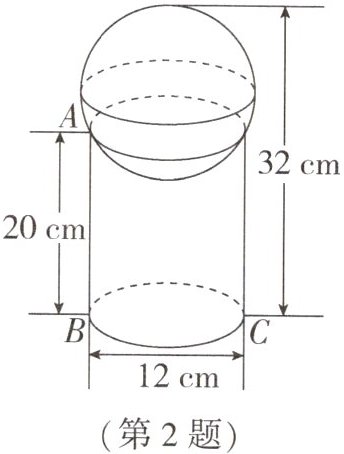
7.5
cm(玻璃瓶厚度忽略不计).
答案:
7.5
3. 如图,点 C 是$\odot O$的优弧 ACB 的中点,弦$AB= 6cm$,E 为 OC 上任意一点,动点 F 从点 A 出发,以每秒 1 cm 的速度沿 AB 方向,从点 A 向点 B 匀速运动,若$y= AE^{2}-EF^{2}$,则 y 与动点 F 的运动时间 x($0≤x≤6$)的函数解析式为______.
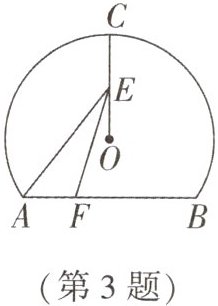

答案:
$y = 6x - x^{2}(0 \leqslant x \leqslant 6)$ 解析: 如图, 延长 $CO$ 交 $AB$ 于点 $G$, $ \because $ 点 $C$ 是 $ \odot O$ 优弧 $ACB$ 的中点, $ \therefore CG \perp AB$, $AG = \frac{1}{2}AB = 3\mathrm{cm}$. 在 $ \mathrm{Rt} \triangle AEG$ 中, $AE^{2} = AG^{2} + EG^{2}$, 在 $ \mathrm{Rt} \triangle EFG$ 中, $EF^{2} = FG^{2} + EG^{2}$, 当 $0 \leqslant x \leqslant 3$ 时, $AF = x\mathrm{cm}$, $FG = (3 - x)\mathrm{cm}$, $y = AE^{2} - EF^{2} = AG^{2} + EG^{2} - FG^{2} - EG^{2} = AG^{2} - FG^{2} = 9 - (3 - x)^{2} = 6x - x^{2}$; 当 $3 < x \leqslant 6$ 时, 设 $AF = x\mathrm{cm}$, 则 $FG = (x - 3)\mathrm{cm}$, $ \therefore y = AE^{2} - EF^{2} = AG^{2} + EG^{2} - FG^{2} - EG^{2} = AG^{2} - FG^{2} = 9 - (x - 3)^{2} = 6x - x^{2}$. 综上, $y = 6x - x^{2}(0 \leqslant x \leqslant 6)$.

$y = 6x - x^{2}(0 \leqslant x \leqslant 6)$ 解析: 如图, 延长 $CO$ 交 $AB$ 于点 $G$, $ \because $ 点 $C$ 是 $ \odot O$ 优弧 $ACB$ 的中点, $ \therefore CG \perp AB$, $AG = \frac{1}{2}AB = 3\mathrm{cm}$. 在 $ \mathrm{Rt} \triangle AEG$ 中, $AE^{2} = AG^{2} + EG^{2}$, 在 $ \mathrm{Rt} \triangle EFG$ 中, $EF^{2} = FG^{2} + EG^{2}$, 当 $0 \leqslant x \leqslant 3$ 时, $AF = x\mathrm{cm}$, $FG = (3 - x)\mathrm{cm}$, $y = AE^{2} - EF^{2} = AG^{2} + EG^{2} - FG^{2} - EG^{2} = AG^{2} - FG^{2} = 9 - (3 - x)^{2} = 6x - x^{2}$; 当 $3 < x \leqslant 6$ 时, 设 $AF = x\mathrm{cm}$, 则 $FG = (x - 3)\mathrm{cm}$, $ \therefore y = AE^{2} - EF^{2} = AG^{2} + EG^{2} - FG^{2} - EG^{2} = AG^{2} - FG^{2} = 9 - (x - 3)^{2} = 6x - x^{2}$. 综上, $y = 6x - x^{2}(0 \leqslant x \leqslant 6)$.

4. (海南中考)如图,在平面直角坐标系中,点 A 的坐标是$(20,0)$,点 B 的坐标是$(16,0)$,点 C,D 在以 OA 为直径的半圆 M 上,且四边形 OCDB 是平行四边形,则点 C 的坐标为______.
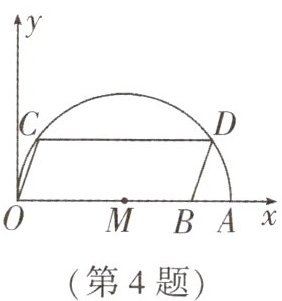

答案:
$(2, 6)$ 解析: $ \because $ 四边形 $OCDB$ 是平行四边形, $B(16, 0)$, $ \therefore CD // OA$, $CD = OB = 16$. 如图, 过点 $M$ 作 $MF \perp CD$ 于点 $F$, 连接 $MC$, 则 $CF = \frac{1}{2}CD = 8$. $ \because OA = 20$, 半径 $MC = \frac{1}{2}OA = 10$, $ \therefore MF = \sqrt{MC^{2} - CF^{2}} = 6$. 过点 $C$ 作 $CE \perp OA$ 于点 $E$, $ \therefore OE = OM - ME = OM - CF = 2$. $ \therefore $ 点 $C$ 的坐标为 $(2, 6)$.

$(2, 6)$ 解析: $ \because $ 四边形 $OCDB$ 是平行四边形, $B(16, 0)$, $ \therefore CD // OA$, $CD = OB = 16$. 如图, 过点 $M$ 作 $MF \perp CD$ 于点 $F$, 连接 $MC$, 则 $CF = \frac{1}{2}CD = 8$. $ \because OA = 20$, 半径 $MC = \frac{1}{2}OA = 10$, $ \therefore MF = \sqrt{MC^{2} - CF^{2}} = 6$. 过点 $C$ 作 $CE \perp OA$ 于点 $E$, $ \therefore OE = OM - ME = OM - CF = 2$. $ \therefore $ 点 $C$ 的坐标为 $(2, 6)$.

5. 教材 P90 习题 T9 变式 (1)如图,在以 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于 C,D 两点.
①求证:$AC= BD;$
②如图②,连接 DO 并延长交小圆于点 E,连接 AE,若$AE= DE$,求$\frac {AD}{BD}$的值.
(2)如图③,过$\odot O$内一点 P 作弦 AB,使$AP= 2BP$.(尺规作图,保留作图痕迹,不写作法)
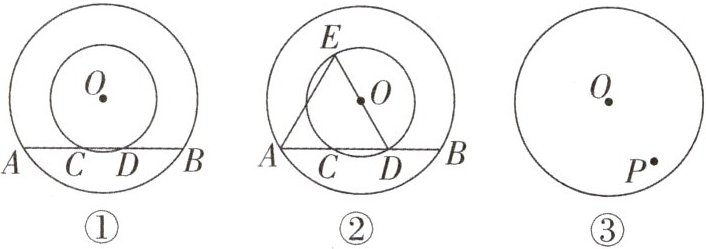
①求证:$AC= BD;$
②如图②,连接 DO 并延长交小圆于点 E,连接 AE,若$AE= DE$,求$\frac {AD}{BD}$的值.
(2)如图③,过$\odot O$内一点 P 作弦 AB,使$AP= 2BP$.(尺规作图,保留作图痕迹,不写作法)

答案:
(1) ① 过点 $O$ 作 $OE \perp AB$ 于点 $E$, 如图 ①. $ \because OE \perp AB$, $OE$ 经过圆心 $O$, $ \therefore EC = ED$, $EA = EB$, $ \therefore AC = BD$.
② 连接 $OC$, 如图 ②. $ \because EA = ED$, $OC = OD$, $ \therefore \angle A = \angle EDA = \angle OCD$, $ \therefore OC // EA$. $ \because OE = OD$, $ \therefore AC = CD$. $ \because AC = DB$, $ \therefore AC = CD = DB$, $ \therefore \frac{AD}{DB} = 2$.
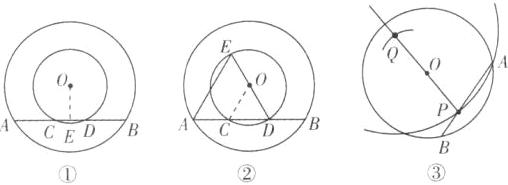
(2) 如图 ③ 所示.
(1) ① 过点 $O$ 作 $OE \perp AB$ 于点 $E$, 如图 ①. $ \because OE \perp AB$, $OE$ 经过圆心 $O$, $ \therefore EC = ED$, $EA = EB$, $ \therefore AC = BD$.
② 连接 $OC$, 如图 ②. $ \because EA = ED$, $OC = OD$, $ \therefore \angle A = \angle EDA = \angle OCD$, $ \therefore OC // EA$. $ \because OE = OD$, $ \therefore AC = CD$. $ \because AC = DB$, $ \therefore AC = CD = DB$, $ \therefore \frac{AD}{DB} = 2$.

(2) 如图 ③ 所示.
6. 在$\odot O$中,AB 为直径,P 是 AB 上一点,$∠NPB= 45^{\circ }$.
(1)如图①,若点 P 与圆心 O 重合,直接写出$\frac {MP^{2}+NP^{2}}{AB^{2}}$的值.
(2)如图②,若$MP= 1,NP= 7$,求$\frac {MP^{2}+NP^{2}}{AB^{2}}$的值.
(3)当点 P 在 AB 上运动时,(2)中的结论是否改变? 若不变,求其值;若变化,求其变化的范围.
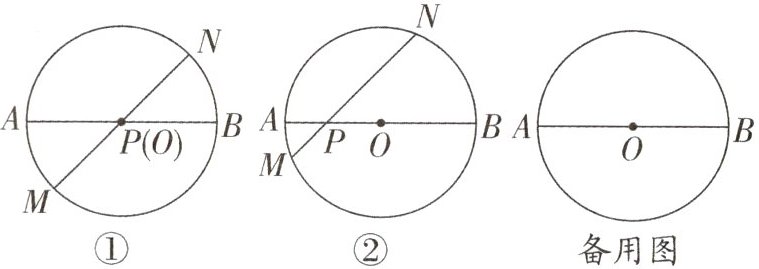
(1)如图①,若点 P 与圆心 O 重合,直接写出$\frac {MP^{2}+NP^{2}}{AB^{2}}$的值.
(2)如图②,若$MP= 1,NP= 7$,求$\frac {MP^{2}+NP^{2}}{AB^{2}}$的值.
(3)当点 P 在 AB 上运动时,(2)中的结论是否改变? 若不变,求其值;若变化,求其变化的范围.

答案:
(1) $ \frac{1}{2} $
(2) 如图 ①, 作 $OH \perp MN$ 于点 $H$, 连接 $ON$, $ \therefore MH = NH = \frac{1}{2}MN = \frac{1}{2}(MP + NP) = \frac{1}{2} \times (1 + 7) = 4$, $ \therefore PH = MH - MP = 4 - 1 = 3$. $ \because \angle NPB = 45^{\circ}$, $ \therefore OH = PH = 3$. 在 $ \mathrm{Rt} \triangle HON$ 中, $ON = \sqrt{OH^{2} + NH^{2}} = \sqrt{3^{2} + 4^{2}} = 5$, $ \therefore AB = 10$, $ \therefore \frac{MP^{2} + NP^{2}}{AB^{2}} = \frac{1^{2} + 7^{2}}{10^{2}} = \frac{1}{2} $.
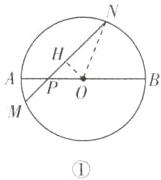
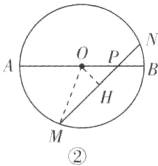
(3)
(2) 中的结论不改变. 作 $OH \perp MN$ 于点 $H$, 连接 $OM$, 如图 ②, 设 $PM = a$, $PN = b$, $ \therefore MH = NH = \frac{a + b}{2} $, $ \therefore PH = NH - PN = \frac{a - b}{2} $. $ \because \angle NPB = 45^{\circ}$, $ \therefore \angle OPH = 45^{\circ}$, $ \therefore OH = PH = \frac{a - b}{2} $. 在 $ \mathrm{Rt} \triangle OMH$ 中, $OM = \sqrt{MH^{2} + OH^{2}} = \sqrt{(\frac{a + b}{2})^{2} + (\frac{a - b}{2})^{2}} = \sqrt{\frac{a^{2} + b^{2}}{2}} $, $ \therefore \frac{MP^{2} + NP^{2}}{AB^{2}} = \frac{a^{2} + b^{2}}{(2\sqrt{\frac{a^{2} + b^{2}}{2}})^{2}} = \frac{1}{2} $.
(1) $ \frac{1}{2} $
(2) 如图 ①, 作 $OH \perp MN$ 于点 $H$, 连接 $ON$, $ \therefore MH = NH = \frac{1}{2}MN = \frac{1}{2}(MP + NP) = \frac{1}{2} \times (1 + 7) = 4$, $ \therefore PH = MH - MP = 4 - 1 = 3$. $ \because \angle NPB = 45^{\circ}$, $ \therefore OH = PH = 3$. 在 $ \mathrm{Rt} \triangle HON$ 中, $ON = \sqrt{OH^{2} + NH^{2}} = \sqrt{3^{2} + 4^{2}} = 5$, $ \therefore AB = 10$, $ \therefore \frac{MP^{2} + NP^{2}}{AB^{2}} = \frac{1^{2} + 7^{2}}{10^{2}} = \frac{1}{2} $.


(3)
(2) 中的结论不改变. 作 $OH \perp MN$ 于点 $H$, 连接 $OM$, 如图 ②, 设 $PM = a$, $PN = b$, $ \therefore MH = NH = \frac{a + b}{2} $, $ \therefore PH = NH - PN = \frac{a - b}{2} $. $ \because \angle NPB = 45^{\circ}$, $ \therefore \angle OPH = 45^{\circ}$, $ \therefore OH = PH = \frac{a - b}{2} $. 在 $ \mathrm{Rt} \triangle OMH$ 中, $OM = \sqrt{MH^{2} + OH^{2}} = \sqrt{(\frac{a + b}{2})^{2} + (\frac{a - b}{2})^{2}} = \sqrt{\frac{a^{2} + b^{2}}{2}} $, $ \therefore \frac{MP^{2} + NP^{2}}{AB^{2}} = \frac{a^{2} + b^{2}}{(2\sqrt{\frac{a^{2} + b^{2}}{2}})^{2}} = \frac{1}{2} $.
查看更多完整答案,请扫码查看


