《2025年学霸题中题九年级数学上册人教版》

1. 下列方程中,一定是关于x的一元二次方程的为(D)
A. $\frac{1}{x^{2}}-\frac{1}{x}-2= 0$
B. $x^{2}+xy+4= 0$
C. $ax^{2}+2x+4= 0$
D. $x^{3}-5= x(x-3)^{2}$

答案： D

2. (聊城中考)用配方法解一元二次方程$2x^{2}-3x-1= 0$,配方正确的是(A)
A. $(x-\frac{3}{4})^{2}= \frac{17}{16}$
B. $(x-\frac{3}{4})^{2}= \frac{1}{2}$
C. $(x-\frac{3}{2})^{2}= \frac{13}{4}$
D. $(x-\frac{3}{2})^{2}= \frac{11}{4}$

答案： A

3. (2024·南通中考)红星村种的水稻2021年平均每公顷产7200kg,2023年平均每公顷产8450kg.求水稻每公顷产量的年平均增长率.设水稻每公顷产量的年平均增长率为x,列方程为(A)
A. $7200(1+x)^{2}= 8450$
B. $7200(1+2x)= 8450$
C. $8450(1-x)^{2}= 7200$
D. $8450(1-2x)= 7200$

答案： A

4. 若关于x的一元二次方程$(m-1)x^{2}+5x+m^{2}-3m+2= 0$的常数项为0,则m等于(B)
A. 1
B. 2
C. 1或2
D. 0

答案： B

5. 若关于x的方程$a(x+m)^{2}+b= 0$的解是$x_{1}= 2$,$x_{2}= -1$(a,m,b均为常数,$a≠0$),则方程$a(-x-m+1)^{2}+b= 0$的解是(C)
A. $x_{1}= 1$,$x_{2}= -2$
B. $x_{1}= 1$,$x_{2}= 0$
C. $x_{1}= 3$,$x_{2}= -2$
D. $x_{1}= 3$,$x_{2}= 0$

答案： C

6. 已知a,b,c是$\triangle ABC$的三边,且满足$a^{2}-b^{2}+ac-bc= 0$,则$\triangle ABC$的形状是(C)
A. 直角三角形
B. 等边三角形
C. 等腰三角形
D. 等腰直角三角形

答案： C

7. (2023·宜宾中考改编)若关于x的方程$x^{2}+(m+1)x+m^{2}= 0$的两个实数根互为倒数,则m的值是(C)
A. -1
B. 1或-1
C. 1
D. 2

答案： C

8. (2024·南京期中)已知m,n,s,t为互不相等的实数,且$(m+s)(m+t)= 2$,$(n+s)(n+t)= 2$,则$mn-st$的值为(A)
A. -2
B. 0
C. $\frac{1}{2}$
D. 2

答案： A

9. 一元二次方程$(1+3x)(x-3)= 2x^{2}+1$化成一般形式后,若二次项系数为1,则一次项系数为-8,常数项为-4.

答案： -8 -4

10. 现定义运算“★”,对于任意实数a,b都有$a★b= a^{2}-3a+b$,如：$3★5= 3^{2}-3×3+5$.若$x★2= 6$,则实数x的值是-1 或 4.

答案： -1 或 4

11. (2023·牡丹江中考)张师傅去年开了一家超市,今年2月份开始盈利,3月份盈利5000元,5月份盈利达到7200元,从3月到5月,每月盈利的平均增长率都相同,则每月盈利的平均增长率是______20%.

答案： 20%

12. (荆州中考)关于x的一元二次方程$x^{2}-2kx+k^{2}-k= 0的两个实数根分别是x_{1}$,$x_{2}$,且$x_{1}^{2}+x_{2}^{2}= 4$,则$x_{1}^{2}-x_{1}x_{2}+x_{2}^{2}$的值是______4.

答案： 4 解析：
∵ $ x ^ { 2 } - 2 k x + k ^ { 2 } - k = 0 $ 的两个实数根分别是 $ x _ { 1 } , x _ { 2 } $，
∴ $ x _ { 1 } + x _ { 2 } = 2 k , x _ { 1 } x _ { 2 } = k ^ { 2 } - k $．
∵ $ x _ { 1 } ^ { 2 } + x _ { 2 } ^ { 2 } = 4 $，
∴ $ ( x _ { 1 } + x _ { 2 } ) ^ { 2 } - 2 x _ { 1 } x _ { 2 } = 4 $，即 $ ( 2 k ) ^ { 2 } - 2 ( k ^ { 2 } - k ) = 4 $，$ 2 k ^ { 2 } + 2 k - 4 = 0 $，$ k ^ { 2 } + k - 2 = 0 $，解得 $ k = - 2 $ 或 1．
∵ $ \Delta = ( - 2 k ) ^ { 2 } - 4 \times 1 \times ( k ^ { 2 } - k ) \geq 0 $，
∴ $ k \geq 0 $，
∴ $ k = 1 $，
∴ $ x _ { 1 } x _ { 2 } = k ^ { 2 } - k = 0 $，
∴ $ x _ { 1 } ^ { 2 } - x _ { 1 } x _ { 2 } + x _ { 2 } ^ { 2 } = 4 - 0 = 4 $．

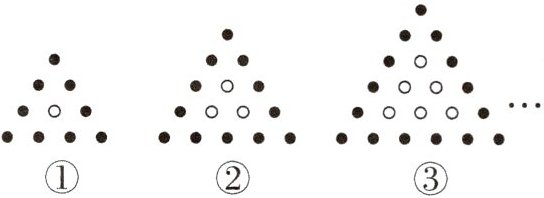
13. 教材P23数学活动变式 用黑、白棋子摆出下列一组图形,根据规律可知：在第n个图形中,黑棋子共有3n+6枚；在第24个图形中,白棋子共有300枚.

答案： $ ( 3 n + 6 ) $ 24