第133页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
8. (宜昌中考改编)如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为2cm,则该莱洛三角形的周长为
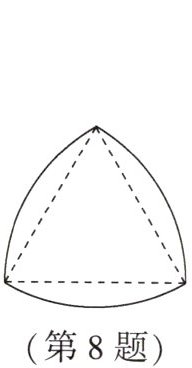
$2π$
cm,面积为$(2π - 2\sqrt{3})$
$cm^{2}$.(圆周率用π表示)
答案:
$2π$ $(2π - 2\sqrt{3})$
9. (自贡中考)如图,直线$y= -2x+2$与坐标轴交于A,B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线$y= -x+3$于点Q,$△OPQ$绕点O顺时针旋转$45^{\circ}$,边PQ扫过区域(阴影部分)面积的最大值是______.
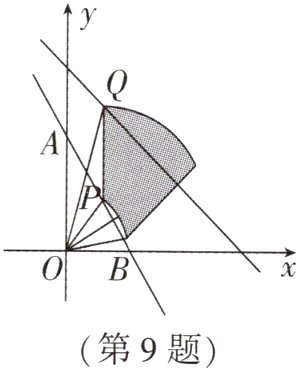

答案:
$\frac {2π}{3}$解析:设$\triangle OPQ$绕点$O$顺时针旋转$45^{\circ }$到$\triangle ODC$的位置,如图所示。设$P(m,-2m + 2)$,则$Q(m,-m + 3)$。
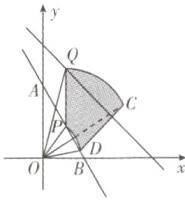
$\therefore OP^{2}=m^{2}+(-2m + 2)^{2}=5m^{2}-8m + 4$,$OQ^{2}=m^{2}+(-m + 3)^{2}=2m^{2}-6m + 9$。
$\because \triangle OPQ$绕点$O$顺时针旋转$45^{\circ }$,$\therefore \triangle OPQ\cong \triangle ODC$,$∠QOC = ∠POD = 45^{\circ }$,$\therefore PQ$扫过区域(阴影部分)面积$S = S_{扇形OQC}-S_{扇形OPD}=\frac {45}{360}×π\cdot OQ^{2}-\frac {45}{360}×π\cdot OP^{2}=\frac {π}{8}(-3m^{2}+2m + 5)=-\frac {3π}{8}(m - \frac {1}{3})^{2}+\frac {2π}{3}$。当$m = \frac {1}{3}$时,$S$的最大值为$\frac {2π}{3}$。
$\frac {2π}{3}$解析:设$\triangle OPQ$绕点$O$顺时针旋转$45^{\circ }$到$\triangle ODC$的位置,如图所示。设$P(m,-2m + 2)$,则$Q(m,-m + 3)$。

$\therefore OP^{2}=m^{2}+(-2m + 2)^{2}=5m^{2}-8m + 4$,$OQ^{2}=m^{2}+(-m + 3)^{2}=2m^{2}-6m + 9$。
$\because \triangle OPQ$绕点$O$顺时针旋转$45^{\circ }$,$\therefore \triangle OPQ\cong \triangle ODC$,$∠QOC = ∠POD = 45^{\circ }$,$\therefore PQ$扫过区域(阴影部分)面积$S = S_{扇形OQC}-S_{扇形OPD}=\frac {45}{360}×π\cdot OQ^{2}-\frac {45}{360}×π\cdot OP^{2}=\frac {π}{8}(-3m^{2}+2m + 5)=-\frac {3π}{8}(m - \frac {1}{3})^{2}+\frac {2π}{3}$。当$m = \frac {1}{3}$时,$S$的最大值为$\frac {2π}{3}$。
$10. ($河北中考$)$如图$,\odot O$的半径为$6,$将该圆周$12$等分后得到表盘模型$,$其中整钟点为$A_{n}(n$为$1~12$的整数$),$过点$A_{7}$作$\odot O$的切线交$A_{1}A_{11}$的延长线于点$P.$
$(1)$通过计算比较直径和劣弧$\overset{\large{\frown}}{A_{7}A_{11}}$的长度哪个更长$.$
$(2)$连接$A_{7}A_{11},$则$A_{7}A_{11}$和$PA_{1}$有什么特殊位置关系$?$请简要说明理由$.$
$(3)$求切线长$PA_{7}$的值$.$
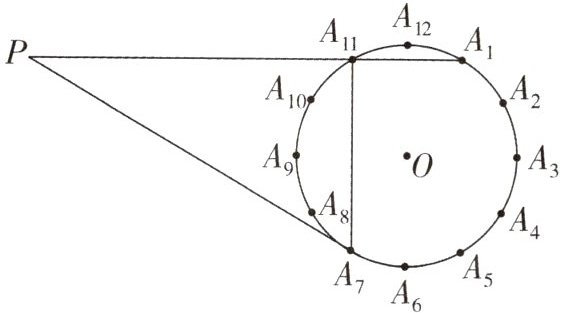
$(1)$通过计算比较直径和劣弧$\overset{\large{\frown}}{A_{7}A_{11}}$的长度哪个更长$.$
$(2)$连接$A_{7}A_{11},$则$A_{7}A_{11}$和$PA_{1}$有什么特殊位置关系$?$请简要说明理由$.$
$(3)$求切线长$PA_{7}$的值$.$

答案:
(1)劣弧$\overset{\frown }{A_{7}A_{11}}=\frac {4}{12}×2π×6 = 4π$,直径$2r = 12$,$\because 4π>12$,故劣弧$\overset{\frown }{A_{7}A_{11}}$更长。
(2)$A_{7}A_{11}⊥PA_{1}$。理由:如图所示,连接$A_{1}A_{7}$,由图可知$A_{1}A_{7}$是直径,$\therefore$对应的圆周角$∠A_{7}A_{11}A_{1}=90^{\circ }$,$\therefore A_{7}A_{11}$和$PA_{1}$互相垂直。
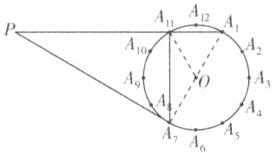
(3)如图所示,连接$A_{11}O$,$∠A_{11}A_{1}A_{7}=\frac {1}{2}∠A_{11}OA_{7}=\frac {1}{2}×\frac {4}{12}×360^{\circ }=60^{\circ }$。$\because PA_{7}$是$\odot O$的切线,$\therefore ∠PA_{7}A_{1}=90^{\circ }$,$\therefore ∠A_{1}PA_{7}=30^{\circ }$,$\therefore PA_{1}=2A_{1}A_{7}=24$,$\therefore PA_{7}=\sqrt {PA_{1}^{2}-A_{1}A_{7}^{2}}=12\sqrt {3}$。
(1)劣弧$\overset{\frown }{A_{7}A_{11}}=\frac {4}{12}×2π×6 = 4π$,直径$2r = 12$,$\because 4π>12$,故劣弧$\overset{\frown }{A_{7}A_{11}}$更长。
(2)$A_{7}A_{11}⊥PA_{1}$。理由:如图所示,连接$A_{1}A_{7}$,由图可知$A_{1}A_{7}$是直径,$\therefore$对应的圆周角$∠A_{7}A_{11}A_{1}=90^{\circ }$,$\therefore A_{7}A_{11}$和$PA_{1}$互相垂直。

(3)如图所示,连接$A_{11}O$,$∠A_{11}A_{1}A_{7}=\frac {1}{2}∠A_{11}OA_{7}=\frac {1}{2}×\frac {4}{12}×360^{\circ }=60^{\circ }$。$\because PA_{7}$是$\odot O$的切线,$\therefore ∠PA_{7}A_{1}=90^{\circ }$,$\therefore ∠A_{1}PA_{7}=30^{\circ }$,$\therefore PA_{1}=2A_{1}A_{7}=24$,$\therefore PA_{7}=\sqrt {PA_{1}^{2}-A_{1}A_{7}^{2}}=12\sqrt {3}$。
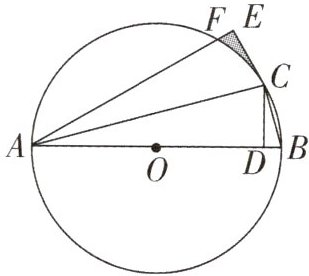
11. (达州中考)如图,AB是$\odot O$的直径,C为$\odot O$上一点(C不与点A,B重合),连接AC,BC,过点C作$CD⊥AB$,垂足为点D.将$△ACD$沿AC翻折,点D落在点E处得$△ACE$,AE交$\odot O$于点F.
(1)求证:CE是$\odot O$的切线;
(2)若$∠BAC= 15^{\circ},OA= 2$,求阴影部分的面积.
(1)求证:CE是$\odot O$的切线;
(2)若$∠BAC= 15^{\circ},OA= 2$,求阴影部分的面积.

答案:
(1)如图,连接$OC$。$\because CD⊥AB$,$\therefore ∠ADC = 90^{\circ }$。$\because \triangle ACD$沿$AC$翻折得到$\triangle ACE$,$\therefore ∠EAC = ∠BAC$,$∠AEC = ∠ADC = 90^{\circ }$。$\because OA = OC$,$\therefore ∠ACO = ∠BAC$,$\therefore ∠ACO = ∠EAC$,$\therefore OC// AE$,$\therefore ∠AEC + ∠ECO = 180^{\circ }$,$\therefore ∠ECO = 90^{\circ }$,即$OC⊥CE$,$\therefore CE$是$\odot O$的切线。
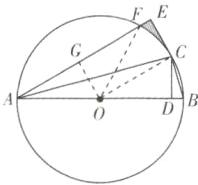
(2)如图,连接$OF$,过点$O$作$OG⊥AE$于点$G$。$\because ∠BAC = 15^{\circ }$,$\therefore ∠BAE = 2∠BAC = 30^{\circ }$,$∠COF = 2∠EAC = 2∠BAC = 30^{\circ }$。$\because OA = 2$,$\therefore OG = \frac {1}{2}OA = 1$,$AG = \sqrt{3}$。$\because OA = OF$,$\therefore AF = 2AG = 2\sqrt{3}$。$\because ∠BOC = 2∠BAC = 30^{\circ }$,$CD⊥AB$,$OC = OA = 2$,$\therefore CD = \frac {1}{2}OC = 1$,$OD = \sqrt{3}$,$\therefore AE = AD = AO + OD = 2 + \sqrt{3}$,$\therefore EF = AE - AF = 2 - \sqrt{3}$,$CE = CD = 1$,$\therefore S_{阴影}=S_{梯形OCEF}-S_{扇形OCF}=\frac {1}{2}×(2 - \sqrt{3}+2)×1-\frac {30}{360}×π×2^{2}=2-\frac {\sqrt{3}}{2}-\frac {1}{3}π$。
(1)如图,连接$OC$。$\because CD⊥AB$,$\therefore ∠ADC = 90^{\circ }$。$\because \triangle ACD$沿$AC$翻折得到$\triangle ACE$,$\therefore ∠EAC = ∠BAC$,$∠AEC = ∠ADC = 90^{\circ }$。$\because OA = OC$,$\therefore ∠ACO = ∠BAC$,$\therefore ∠ACO = ∠EAC$,$\therefore OC// AE$,$\therefore ∠AEC + ∠ECO = 180^{\circ }$,$\therefore ∠ECO = 90^{\circ }$,即$OC⊥CE$,$\therefore CE$是$\odot O$的切线。

(2)如图,连接$OF$,过点$O$作$OG⊥AE$于点$G$。$\because ∠BAC = 15^{\circ }$,$\therefore ∠BAE = 2∠BAC = 30^{\circ }$,$∠COF = 2∠EAC = 2∠BAC = 30^{\circ }$。$\because OA = 2$,$\therefore OG = \frac {1}{2}OA = 1$,$AG = \sqrt{3}$。$\because OA = OF$,$\therefore AF = 2AG = 2\sqrt{3}$。$\because ∠BOC = 2∠BAC = 30^{\circ }$,$CD⊥AB$,$OC = OA = 2$,$\therefore CD = \frac {1}{2}OC = 1$,$OD = \sqrt{3}$,$\therefore AE = AD = AO + OD = 2 + \sqrt{3}$,$\therefore EF = AE - AF = 2 - \sqrt{3}$,$CE = CD = 1$,$\therefore S_{阴影}=S_{梯形OCEF}-S_{扇形OCF}=\frac {1}{2}×(2 - \sqrt{3}+2)×1-\frac {30}{360}×π×2^{2}=2-\frac {\sqrt{3}}{2}-\frac {1}{3}π$。
12. 教材P123复习题T6变式(聊城中考)如图,线段$AB= 2$,以AB为直径画半圆,圆心为$A_{1}$,以$AA_{1}$为直径画半圆①;取$A_{1}B的中点A_{2}$,以$A_{1}A_{2}$为直径画半圆②;取$A_{2}B的中点A_{3}$,以$A_{2}A_{3}$为直径画半圆③……按照这样的规律画下去,大半圆内部依次画出的8个小半圆的弧长之和为______
$\frac {255}{256}π$
.
答案:
$\frac {255}{256}π$解析:$\because AB = 2$,$\therefore AA_{1}=1$,半圆①的弧长为$\frac {π×1}{2}=\frac {1}{2}π$,同理$A_{1}A_{2}=\frac {1}{2}$,半圆②的弧长为$\frac {π×\frac {1}{2}}{2}=(\frac {1}{2})^{2}π$,$A_{2}A_{3}=\frac {1}{4}$,半圆③的弧长为$\frac {π×\frac {1}{4}}{2}=(\frac {1}{2})^{3}π$……半圆⑧的弧长为$\frac {π×(\frac {1}{2})^{7}}{2}=(\frac {1}{2})^{8}π$,$\therefore 8$个小半圆的弧长之和为$\frac {1}{2}π+(\frac {1}{2})^{2}π+(\frac {1}{2})^{3}π+... +(\frac {1}{2})^{8}π=\frac {255}{256}π$。
13. 如图,将半径为2,圆心角为$120^{\circ}$的扇形OAB绕点A逆时针旋转$60^{\circ}$,点O,B的对应点分别为$O',B'$,连接$BB'$,则图中阴影部分的面积是______
$2\sqrt{3}-\frac {2π}{3}$
.
答案:
$2\sqrt{3}-\frac {2π}{3}$解析:连接$OO'$,$BO'$,$\because$将半径为$2$,圆心角为$120^{\circ }$的扇形$OAB$绕点$A$逆时针旋转$60^{\circ }$,$\therefore ∠OAO' = 60^{\circ }$,$\therefore \triangle OAO'$是等边三角形,$\therefore ∠AOO' = ∠AO'O = 60^{\circ }$。$\because ∠AOB = 120^{\circ }$,$\therefore ∠O'OB = 60^{\circ }$,$\therefore \triangle OO'B$是等边三角形,$\therefore ∠AO'B = 120^{\circ }$。$\because ∠AO'B' = 120^{\circ }$,$\therefore ∠AO'O + ∠AO'B' = 180^{\circ }$,$\therefore O$,$O'$,$B'$三点共线,$\therefore ∠B'O'B = 120^{\circ }$。又$\because O'B' = O'B$,$\therefore ∠O'B'B = ∠O'BB' = 30^{\circ }$。过点$O'$作$O'C⊥BB'$,垂足为$C$,易得$O'C = 1$,$BB' = 2\sqrt{3}$,$\therefore$题图中阴影部分的面积$=S_{\triangle B'O'B}-(S_{扇形OO'B}-S_{\triangle OO'B})=\frac {1}{2}×1×2\sqrt{3}-(\frac {60π\cdot 2^{2}}{360}-\frac {1}{2}×2×\sqrt{3})=2\sqrt{3}-\frac {2π}{3}$。
查看更多完整答案,请扫码查看


