第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
1. 利用十字相乘法解方程.
(1)$x^{2}-x-90= 0$;
(2)$2x^{2}+x-10= 0$;
(1)$x^{2}-x-90= 0$;
方程整理得$(x - 10)(x + 9) = 0$,解得$x_1 = 10$,$x_2 = -9$
(2)$2x^{2}+x-10= 0$;
方程整理得$(2x + 5)(x - 2) = 0$,解得$x_1 = -2.5$,$x_2 = 2$
答案:
(1) 方程整理得$(x - 10)(x + 9) = 0$,解得$x_1 = 10$,$x_2 = -9$。
(2) 方程整理得$(2x + 5)(x - 2) = 0$,解得$x_1 = -2.5$,$x_2 = 2$。
(1) 方程整理得$(x - 10)(x + 9) = 0$,解得$x_1 = 10$,$x_2 = -9$。
(2) 方程整理得$(2x + 5)(x - 2) = 0$,解得$x_1 = -2.5$,$x_2 = 2$。
2. 改编题 利用换元法解方程.
(1)倒数换元:$\frac {x-2}{x}-\frac {3x}{x-2}= 2$;
(2)整体换元:$(x-1)(x-2)(x-3)(x-4)= 48$;
(3)指数换元:$x^{x^{4}}= 64$;
(4)根式换元:$3x^{2}+2x\sqrt {2x^{2}+5x-2}+5x-38= 0$;
(5)降次换元:$6x^{4}-35x^{3}+62x^{2}-35x+6= 0$;
(6)均值换元:$(x+1)^{4}+(x+3)^{4}= 706$。
(1)倒数换元:$\frac {x-2}{x}-\frac {3x}{x-2}= 2$;
设$\frac{x - 2}{x} = y$,则原方程可化为$y - \frac{3}{y} = 2$,整理得$y^2 - 2y - 3 = 0$,解得$y_1 = 3$,$y_2 = -1$。当$y = 3$时,$\frac{x - 2}{x} = 3$,解得$x = -1$;当$y = -1$时,$\frac{x - 2}{x} = -1$,解得$x = 1$。经检验,$x = \pm 1$都是原方程的根,∴原方程的根为$x_1 = 1$,$x_2 = -1$。
(2)整体换元:$(x-1)(x-2)(x-3)(x-4)= 48$;
$(x - 1)(x - 2)(x - 3)(x - 4) = 48$,$(x^2 - 5x + 4)(x^2 - 5x + 6) = 48$,设$x^2 - 5x = t$,则$(t + 4)(t + 6) = 48$,整理得$t^2 + 10t - 24 = 0$,$(t + 12)(t - 2) = 0$,解得$t_1 = -12$,$t_2 = 2$。当$t = -12$,即$x^2 - 5x = -12$时,$x^2 - 5x + 12 = 0$,无实数解;当$t = 2$,即$x^2 - 5x = 2$时,解得$x_1 = \frac{5 + \sqrt{33}}{2}$,$x_2 = \frac{5 - \sqrt{33}}{2}$。故原方程的解为$x_1 = \frac{5 + \sqrt{33}}{2}$,$x_2 = \frac{5 - \sqrt{33}}{2}$。
(3)指数换元:$x^{x^{4}}= 64$;
设$x^4 = t$,则$x^t = 64$,$\therefore (x^t)^4 = 64^4$,$\therefore (x^4)^t = 64^4$,$\therefore t^t = (8^2)^4 = 8^8$,$\therefore t = 8 = x^4$,$\therefore x = \pm \sqrt[4]{8}$。
(4)根式换元:$3x^{2}+2x\sqrt {2x^{2}+5x-2}+5x-38= 0$;
设$\sqrt{2x^2 + 5x - 2} = y$,$2x^2 + 5x - 2 = y^2$,$5x = y^2 + 2 - 2x^2$,原方程可化为$3x^2 + 2xy + (y^2 + 2 - 2x^2) - 38 = 0$,整理得$x^2 + 2xy + y^2 - 36 = 0$,即$x + y = \pm 6$。当$x + y = 6$时,$x + \sqrt{2x^2 + 5x - 2} = 6$,即$\sqrt{2x^2 + 5x - 2} = 6 - x$,等号两边同时平方,整理得$x^2 + 17x - 38 = 0$,解得$x_1 = 2$,$x_2 = -19$,经检验都是原方程的根;当$x + y = -6$时,$x + \sqrt{2x^2 + 5x - 2} = -6$,即$\sqrt{2x^2 + 5x - 2} = -6 - x$,等号两边同时平方,整理得$x^2 - 7x - 38 = 0$,解得$x = \frac{7 \pm \sqrt{201}}{2}$,经检验,$x = \frac{7 \pm \sqrt{201}}{2}$都不是$x + \sqrt{2x^2 + 5x - 2} = -6$的根,舍去。故原方程的解为$x_1 = 2$,$x_2 = -19$。
(5)降次换元:$6x^{4}-35x^{3}+62x^{2}-35x+6= 0$;
经验证$x = 0$不是方程$6x^4 - 35x^3 + 62x^2 - 35x + 6 = 0$的根,原方程两边同时除以$x^2$,得$6x^2 - 35x + 62 - \frac{35}{x} + \frac{6}{x^2} = 0$,即$6(x^2 + \frac{1}{x^2}) - 35(x + \frac{1}{x}) + 62 = 0$,设$x + \frac{1}{x} = y$,则$x^2 + 2 + \frac{1}{x^2} = y^2$,$\therefore x^2 + \frac{1}{x^2} = y^2 - 2$,则原方程可化为$6(y^2 - 2) - 35y + 62 = 0$,$6y^2 - 35y + 50 = 0$,$(2y - 5)(3y - 10) = 0$,$y_1 = \frac{5}{2}$,$y_2 = \frac{10}{3}$,当$y = \frac{5}{2}$时,$x + \frac{1}{x} = \frac{5}{2}$,解得$x = 2$或$\frac{1}{2}$;当$y = \frac{10}{3}$时,$x + \frac{1}{x} = \frac{10}{3}$,解得$x = 3$或$\frac{1}{3}$。经检验,原方程的解为$x_1 = 2$,$x_2 = \frac{1}{2}$,$x_3 = 3$,$x_4 = \frac{1}{3}$
(6)均值换元:$(x+1)^{4}+(x+3)^{4}= 706$。
设$y = x + 2$,原方程可化为$(y - 1)^4 + (y + 1)^4 = 706$,$\therefore (y^2 - 2y + 1)^2 + (y^2 + 2y + 1)^2 = 706$,$\therefore y^4 + 4y^2 + 1 - 4y^3 + 2y^2 - 4y + y^4 + 4y^2 + 1 + 4y^3 + 2y^2 + 4y = 706$,整理得$2y^4 + 12y^2 - 704 = 0$,解得$y^2 = 16$或$y^2 = -22$(舍去),$\therefore y = \pm 4$, $\therefore x + 2 = \pm 4$, $\therefore x = 2$或$x = -6$。
答案:
(1) 设$\frac{x - 2}{x} = y$,则原方程可化为$y - \frac{3}{y} = 2$,整理得$y^2 - 2y - 3 = 0$,解得$y_1 = 3$,$y_2 = -1$。当$y = 3$时,$\frac{x - 2}{x} = 3$,解得$x = -1$;当$y = -1$时,$\frac{x - 2}{x} = -1$,解得$x = 1$。经检验,$x = \pm 1$都是原方程的根,
∴原方程的根为$x_1 = 1$,$x_2 = -1$。
(2) $(x - 1)(x - 2)(x - 3)(x - 4) = 48$,$(x^2 - 5x + 4)(x^2 - 5x + 6) = 48$,设$x^2 - 5x = t$,则$(t + 4)(t + 6) = 48$,整理得$t^2 + 10t - 24 = 0$,$(t + 12)(t - 2) = 0$,解得$t_1 = -12$,$t_2 = 2$。当$t = -12$,即$x^2 - 5x = -12$时,$x^2 - 5x + 12 = 0$,无实数解;当$t = 2$,即$x^2 - 5x = 2$时,解得$x_1 = \frac{5 + \sqrt{33}}{2}$,$x_2 = \frac{5 - \sqrt{33}}{2}$。故原方程的解为$x_1 = \frac{5 + \sqrt{33}}{2}$,$x_2 = \frac{5 - \sqrt{33}}{2}$。
(3) 设$x^4 = t$,则$x^t = 64$,$\therefore (x^t)^4 = 64^4$,$\therefore (x^4)^t = 64^4$,$\therefore t^t = (8^2)^4 = 8^8$,$\therefore t = 8 = x^4$,$\therefore x = \pm \sqrt[4]{8}$。
(4) 设$\sqrt{2x^2 + 5x - 2} = y$,$2x^2 + 5x - 2 = y^2$,$5x = y^2 + 2 - 2x^2$,原方程可化为$3x^2 + 2xy + (y^2 + 2 - 2x^2) - 38 = 0$,整理得$x^2 + 2xy + y^2 - 36 = 0$,即$x + y = \pm 6$。
当$x + y = 6$时,$x + \sqrt{2x^2 + 5x - 2} = 6$,即$\sqrt{2x^2 + 5x - 2} = 6 - x$,等号两边同时平方,整理得$x^2 + 17x - 38 = 0$,解得$x_1 = 2$,$x_2 = -19$,经检验都是原方程的根;
当$x + y = -6$时,$x + \sqrt{2x^2 + 5x - 2} = -6$,即$\sqrt{2x^2 + 5x - 2} = -6 - x$,等号两边同时平方,整理得$x^2 - 7x - 38 = 0$,解得$x = \frac{7 \pm \sqrt{201}}{2}$,经检验,$x = \frac{7 \pm \sqrt{201}}{2}$都不是$x + \sqrt{2x^2 + 5x - 2} = -6$的根,舍去。
故原方程的解为$x_1 = 2$,$x_2 = -19$。
(5) 经验证$x = 0$不是方程$6x^4 - 35x^3 + 62x^2 - 35x + 6 = 0$的根,原方程两边同时除以$x^2$,得$6x^2 - 35x + 62 - \frac{35}{x} + \frac{6}{x^2} = 0$,即$6(x^2 + \frac{1}{x^2}) - 35(x + \frac{1}{x}) + 62 = 0$,设$x + \frac{1}{x} = y$,则$x^2 + 2 + \frac{1}{x^2} = y^2$,$\therefore x^2 + \frac{1}{x^2} = y^2 - 2$,则原方程可化为$6(y^2 - 2) - 35y + 62 = 0$,$6y^2 - 35y + 50 = 0$,$(2y - 5)(3y - 10) = 0$,$y_1 = \frac{5}{2}$,$y_2 = \frac{10}{3}$,当$y = \frac{5}{2}$时,$x + \frac{1}{x} = \frac{5}{2}$,解得$x = 2$或$\frac{1}{2}$;当$y = \frac{10}{3}$时,$x + \frac{1}{x} = \frac{10}{3}$,解得$x = 3$或$\frac{1}{3}$。经检验,原方程的解为$x_1 = 2$,$x_2 = \frac{1}{2}$,$x_3 = 3$,$x_4 = \frac{1}{3}$。
(6) 设$y = x + 2$,原方程可化为$(y - 1)^4 + (y + 1)^4 = 706$,$\therefore (y^2 - 2y + 1)^2 + (y^2 + 2y + 1)^2 = 706$,$\therefore y^4 + 4y^2 + 1 - 4y^3 + 2y^2 - 4y + y^4 + 4y^2 + 1 + 4y^3 + 2y^2 + 4y = 706$,整理得$2y^4 + 12y^2 - 704 = 0$,解得$y^2 = 16$或$y^2 = -22$(舍去),$\therefore y = \pm 4$,即$x + 2 = \pm 4$,$\therefore x = 2$或$x = -6$。
知识拓展
若实数$x$,$y$满足$x + y = p$,则可设$x = \frac{p}{2} + t$,$y = \frac{p}{2} - t$,这种换元方法被称为“均值换元法”。例如,解形如$(x + a)^4 + (x + b)^4 = c$的一元四次方程时,即可用均值换元法,先求常数$a$和$b$的均值$\frac{a + b}{2}$,设$y = x + \frac{a + b}{2}$,这样可以消去含未知数的奇次项,使方程转化成易于求解的双二次方程。
(1) 设$\frac{x - 2}{x} = y$,则原方程可化为$y - \frac{3}{y} = 2$,整理得$y^2 - 2y - 3 = 0$,解得$y_1 = 3$,$y_2 = -1$。当$y = 3$时,$\frac{x - 2}{x} = 3$,解得$x = -1$;当$y = -1$时,$\frac{x - 2}{x} = -1$,解得$x = 1$。经检验,$x = \pm 1$都是原方程的根,
∴原方程的根为$x_1 = 1$,$x_2 = -1$。
(2) $(x - 1)(x - 2)(x - 3)(x - 4) = 48$,$(x^2 - 5x + 4)(x^2 - 5x + 6) = 48$,设$x^2 - 5x = t$,则$(t + 4)(t + 6) = 48$,整理得$t^2 + 10t - 24 = 0$,$(t + 12)(t - 2) = 0$,解得$t_1 = -12$,$t_2 = 2$。当$t = -12$,即$x^2 - 5x = -12$时,$x^2 - 5x + 12 = 0$,无实数解;当$t = 2$,即$x^2 - 5x = 2$时,解得$x_1 = \frac{5 + \sqrt{33}}{2}$,$x_2 = \frac{5 - \sqrt{33}}{2}$。故原方程的解为$x_1 = \frac{5 + \sqrt{33}}{2}$,$x_2 = \frac{5 - \sqrt{33}}{2}$。
(3) 设$x^4 = t$,则$x^t = 64$,$\therefore (x^t)^4 = 64^4$,$\therefore (x^4)^t = 64^4$,$\therefore t^t = (8^2)^4 = 8^8$,$\therefore t = 8 = x^4$,$\therefore x = \pm \sqrt[4]{8}$。
(4) 设$\sqrt{2x^2 + 5x - 2} = y$,$2x^2 + 5x - 2 = y^2$,$5x = y^2 + 2 - 2x^2$,原方程可化为$3x^2 + 2xy + (y^2 + 2 - 2x^2) - 38 = 0$,整理得$x^2 + 2xy + y^2 - 36 = 0$,即$x + y = \pm 6$。
当$x + y = 6$时,$x + \sqrt{2x^2 + 5x - 2} = 6$,即$\sqrt{2x^2 + 5x - 2} = 6 - x$,等号两边同时平方,整理得$x^2 + 17x - 38 = 0$,解得$x_1 = 2$,$x_2 = -19$,经检验都是原方程的根;
当$x + y = -6$时,$x + \sqrt{2x^2 + 5x - 2} = -6$,即$\sqrt{2x^2 + 5x - 2} = -6 - x$,等号两边同时平方,整理得$x^2 - 7x - 38 = 0$,解得$x = \frac{7 \pm \sqrt{201}}{2}$,经检验,$x = \frac{7 \pm \sqrt{201}}{2}$都不是$x + \sqrt{2x^2 + 5x - 2} = -6$的根,舍去。
故原方程的解为$x_1 = 2$,$x_2 = -19$。
(5) 经验证$x = 0$不是方程$6x^4 - 35x^3 + 62x^2 - 35x + 6 = 0$的根,原方程两边同时除以$x^2$,得$6x^2 - 35x + 62 - \frac{35}{x} + \frac{6}{x^2} = 0$,即$6(x^2 + \frac{1}{x^2}) - 35(x + \frac{1}{x}) + 62 = 0$,设$x + \frac{1}{x} = y$,则$x^2 + 2 + \frac{1}{x^2} = y^2$,$\therefore x^2 + \frac{1}{x^2} = y^2 - 2$,则原方程可化为$6(y^2 - 2) - 35y + 62 = 0$,$6y^2 - 35y + 50 = 0$,$(2y - 5)(3y - 10) = 0$,$y_1 = \frac{5}{2}$,$y_2 = \frac{10}{3}$,当$y = \frac{5}{2}$时,$x + \frac{1}{x} = \frac{5}{2}$,解得$x = 2$或$\frac{1}{2}$;当$y = \frac{10}{3}$时,$x + \frac{1}{x} = \frac{10}{3}$,解得$x = 3$或$\frac{1}{3}$。经检验,原方程的解为$x_1 = 2$,$x_2 = \frac{1}{2}$,$x_3 = 3$,$x_4 = \frac{1}{3}$。
(6) 设$y = x + 2$,原方程可化为$(y - 1)^4 + (y + 1)^4 = 706$,$\therefore (y^2 - 2y + 1)^2 + (y^2 + 2y + 1)^2 = 706$,$\therefore y^4 + 4y^2 + 1 - 4y^3 + 2y^2 - 4y + y^4 + 4y^2 + 1 + 4y^3 + 2y^2 + 4y = 706$,整理得$2y^4 + 12y^2 - 704 = 0$,解得$y^2 = 16$或$y^2 = -22$(舍去),$\therefore y = \pm 4$,即$x + 2 = \pm 4$,$\therefore x = 2$或$x = -6$。
知识拓展
若实数$x$,$y$满足$x + y = p$,则可设$x = \frac{p}{2} + t$,$y = \frac{p}{2} - t$,这种换元方法被称为“均值换元法”。例如,解形如$(x + a)^4 + (x + b)^4 = c$的一元四次方程时,即可用均值换元法,先求常数$a$和$b$的均值$\frac{a + b}{2}$,设$y = x + \frac{a + b}{2}$,这样可以消去含未知数的奇次项,使方程转化成易于求解的双二次方程。
3. 我国三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载了解方程$x^{2}+5x-14= 0(x>0)$,即$x(x+5)= 14(x>0)$的方法.首先构造了如图①所示的图形,图中的大正方形面积是$(x+x+5)^{2}$,其中四个全等的小矩形面积分别为$x(x+5)= 14$,中间的小正方形面积为$5^{2}$,所以大正方形的面积又可表示为$4×14+5^{2}= 81$,据此易得$x= 2$.

(1)参照上述方法,请在三个构图中选择能够说明方程$x^{2}-3x-10= 0(x>0)$解法的正确构图
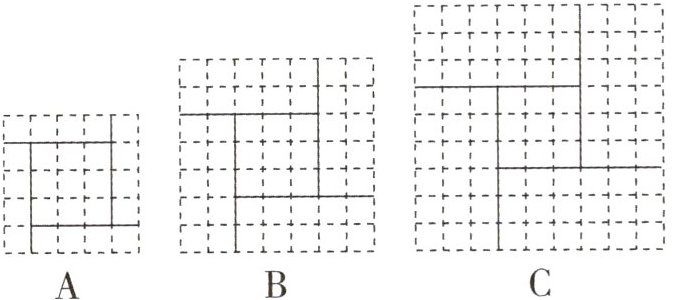
是____.
(2)请你结合上述问题的学习,在图②的网格中设计用几何法求解方程$x^{2}-2x-15= 0(x>0)$的构图(类比图①标明相关数据,不需写出解答过程).


(1)参照上述方法,请在三个构图中选择能够说明方程$x^{2}-3x-10= 0(x>0)$解法的正确构图

是____.
(2)请你结合上述问题的学习,在图②的网格中设计用几何法求解方程$x^{2}-2x-15= 0(x>0)$的构图(类比图①标明相关数据,不需写出解答过程).

答案:
(1) B
(2) 如图所示,

(1) B
(2) 如图所示,

4. 原创题 解方程.
(1)$x^{2}+2|x|-1= 0$;
(2)$x^{2}-|2x-1|-4= 0$.
(1)$x^{2}+2|x|-1= 0$;
$x_1 = \sqrt{2} - 1$,$x_2 = -\sqrt{2} + 1$
(2)$x^{2}-|2x-1|-4= 0$.
$x_1 = 3$,$x_2 = -1 - \sqrt{6}$
答案:
(1) 解法一:当$x \geq 0$时,原方程为$x^2 + 2x - 1 = 0$,解得$x_1 = \sqrt{2} - 1$,$x_2 = -\sqrt{2} - 1$(舍去);当$x < 0$时,原方程为$x^2 - 2x - 1 = 0$,解得$x_1 = \sqrt{2} + 1$(舍去),$x_2 = -\sqrt{2} + 1$。综上,$x_1 = \sqrt{2} - 1$,$x_2 = -\sqrt{2} + 1$。
解法二:把原方程看作关于$|x|$的一元二次方程,$(|x|)^2 + 2|x| - 1 = 0$,解方程得$|x| = -1 + \sqrt{2}$或$|x| = -1 - \sqrt{2}$(舍去),$\therefore x_1 = -1 + \sqrt{2}$,$x_2 = 1 - \sqrt{2}$。
(2) 当$2x - 1 \geq 0$,即$x \geq \frac{1}{2}$时,$x^2 - |2x - 1| - 4 = 0$可化为$x^2 - 2x - 3 = 0$,解得$x_1 = 3$,$x_2 = -1$(舍去);当$2x - 1 < 0$,即$x < \frac{1}{2}$时,$x^2 - |2x - 1| - 4 = 0$可化为$x^2 + 2x - 5 = 0$,解得$x_1 = -1 + \sqrt{6}$(舍去),$x_2 = -1 - \sqrt{6}$。综上,$x_1 = 3$,$x_2 = -1 - \sqrt{6}$。
归纳总结
解含有绝对值的一元二次方程,一般利用绝对值的性质$|x| = \begin{cases} x(x \geq 0) \\ -x(x < 0) \end{cases}$,进行分类讨论,将含绝对值的一元二次方程转化为一般的一元二次方程;有时也可以利用绝对值的性质$(x^2 = |x|^2)$,直接把原方程转化为关于$|x|$的一元二次方程。
(1) 解法一:当$x \geq 0$时,原方程为$x^2 + 2x - 1 = 0$,解得$x_1 = \sqrt{2} - 1$,$x_2 = -\sqrt{2} - 1$(舍去);当$x < 0$时,原方程为$x^2 - 2x - 1 = 0$,解得$x_1 = \sqrt{2} + 1$(舍去),$x_2 = -\sqrt{2} + 1$。综上,$x_1 = \sqrt{2} - 1$,$x_2 = -\sqrt{2} + 1$。
解法二:把原方程看作关于$|x|$的一元二次方程,$(|x|)^2 + 2|x| - 1 = 0$,解方程得$|x| = -1 + \sqrt{2}$或$|x| = -1 - \sqrt{2}$(舍去),$\therefore x_1 = -1 + \sqrt{2}$,$x_2 = 1 - \sqrt{2}$。
(2) 当$2x - 1 \geq 0$,即$x \geq \frac{1}{2}$时,$x^2 - |2x - 1| - 4 = 0$可化为$x^2 - 2x - 3 = 0$,解得$x_1 = 3$,$x_2 = -1$(舍去);当$2x - 1 < 0$,即$x < \frac{1}{2}$时,$x^2 - |2x - 1| - 4 = 0$可化为$x^2 + 2x - 5 = 0$,解得$x_1 = -1 + \sqrt{6}$(舍去),$x_2 = -1 - \sqrt{6}$。综上,$x_1 = 3$,$x_2 = -1 - \sqrt{6}$。
归纳总结
解含有绝对值的一元二次方程,一般利用绝对值的性质$|x| = \begin{cases} x(x \geq 0) \\ -x(x < 0) \end{cases}$,进行分类讨论,将含绝对值的一元二次方程转化为一般的一元二次方程;有时也可以利用绝对值的性质$(x^2 = |x|^2)$,直接把原方程转化为关于$|x|$的一元二次方程。
5. (1)若关于x的方程$x^{2}-2|x|+2= m$恰有3个不相等的实数根,则m的值为
(2)若关于x的方程$|x^{2}+ax|= 4$只有3个不相等的实数根,则这3个根为
2
.(2)若关于x的方程$|x^{2}+ax|= 4$只有3个不相等的实数根,则这3个根为
$-2 \pm 2\sqrt{2}$,$-2$或$2 \pm 2\sqrt{2}$,2
.
答案:
(1) 2
(2) $-2 \pm 2\sqrt{2}$,$-2$或$2 \pm 2\sqrt{2}$,2 解析:$\because |x^2 + ax| = 4$,$\therefore x^2 + ax - 4 = 0$ ①或$x^2 + ax + 4 = 0$ ②。方程①②不可能有相同的根,而原方程有3个不相等的实数根,$\therefore$方程①②中有一个含有等根,而$\Delta_1 = a^2 + 16 > 0$,$\therefore \Delta_2 = a^2 - 16 = 0$,$\therefore a = \pm 4$。当$a = 4$时,原方程为$x^2 + 4x - 4 = 0$或$x^2 + 4x + 4 = 0$,原方程的解为$x = -2 \pm 2\sqrt{2}$或$x = -2$;当$a = -4$时,原方程为$x^2 - 4x - 4 = 0$或$x^2 - 4x + 4 = 0$,原方程的解为$x = 2 \pm 2\sqrt{2}$或$x = 2$。
知识拓展
重根的概念仅存在于代数方程(也称多项式方程),带绝对值的方程没有重根,相等的根都视为一个根。
(1) 2
(2) $-2 \pm 2\sqrt{2}$,$-2$或$2 \pm 2\sqrt{2}$,2 解析:$\because |x^2 + ax| = 4$,$\therefore x^2 + ax - 4 = 0$ ①或$x^2 + ax + 4 = 0$ ②。方程①②不可能有相同的根,而原方程有3个不相等的实数根,$\therefore$方程①②中有一个含有等根,而$\Delta_1 = a^2 + 16 > 0$,$\therefore \Delta_2 = a^2 - 16 = 0$,$\therefore a = \pm 4$。当$a = 4$时,原方程为$x^2 + 4x - 4 = 0$或$x^2 + 4x + 4 = 0$,原方程的解为$x = -2 \pm 2\sqrt{2}$或$x = -2$;当$a = -4$时,原方程为$x^2 - 4x - 4 = 0$或$x^2 - 4x + 4 = 0$,原方程的解为$x = 2 \pm 2\sqrt{2}$或$x = 2$。
知识拓展
重根的概念仅存在于代数方程(也称多项式方程),带绝对值的方程没有重根,相等的根都视为一个根。
查看更多完整答案,请扫码查看


